Jump to content

Axiom (computer algebra system)

From Wikipedia, the free encyclopedia
Axiom
Developer(s)Independent group of people
Stable release
Latest Docker release / November 13, 2015; 8 years ago (2015-11-13)[1]
Preview release
Sourceforge master / February 6, 2022; 2 years ago (2022-02-06)
Repositoryhttps://sourceforge.net/p/axiom/code/
Written inLisp
Operating systemCross-platform
TypeComputer algebra system
LicenseModified BSD License
Websitewww.axiom-developer.org

Axiom is a free, general-purpose computer algebra system. It consists of an interpreter environment, a compiler and a library, which defines a strongly typed hierarchy.

History[edit]

Two computer algebra systems named Scratchpad were developed by IBM. The first one was started in 1965 by James Griesmer[2] at the request of Ralph Gomory, and written in Fortran.[3] The development of this software was stopped before any public release. The second Scratchpad, originally named Scratchpad II, was developed from 1977 on, at Thomas J. Watson Research Center, under the direction of Richard Dimick Jenks.[4]

The design is principally due to Richard D. Jenks (IBM Research), James H. Davenport (University of Bath), Barry M. Trager (IBM Research), David Y.Y. Yun (Southern Methodist University) and Victor S. Miller (IBM Research). Early consultants on the project were David Barton (University of California, Berkeley) and James W. Thatcher (IBM Research). Implementation included Robert Sutor (IBM Research), Scott C. Morrison (University of California, Berkeley), Christine J. Sundaresan (IBM Research), Timothy Daly (IBM Research), Patrizia Gianni (University of Pisa), Albrecht Fortenbacher (Universitaet Karlsruhe), Stephen M. Watt (IBM Research and University of Waterloo), Josh Cohen (Yale University), Michael Rothstein (Kent State University), Manuel Bronstein (IBM Research), Michael Monagan (Simon Fraser University), Jonathan Steinbach (IBM Research), William Burge (IBM Research), Jim Wen (IBM Research), William Sit (City College of New York), and Clifton Williamson (IBM Research)[5]

Scratchpad II was renamed Axiom when IBM decided, circa 1990, to make it a commercial product. A few years later, it was sold to NAG. In 2001, it was withdrawn from the market and re-released under the Modified BSD License. Since then, the project's lead developer has been Tim Daly.

In 2007, Axiom was forked twice, originating two different open-source projects: OpenAxiom[6] and FriCAS,[7] following "serious disagreement about project goals".[8] The Axiom project continued to be developed by Tim Daly.

The current research direction is "Proving Axiom Sane", that is, logical, rational, judicious, and sound.

Design[edit]

In Axiom, each object has a type. Examples of types are mathematical structures (such as rings, fields, polynomials) as well as data structures from computer science (e.g., lists, trees, hash tables).

A function can take a type as argument, and its return value can also be a type. For example, Fraction is a function, that takes an IntegralDomain as argument, and returns the field of fractions of its argument. As another example, the ring of matrices with rational entries would be constructed as SquareMatrix(4, Fraction Integer). Of course, when working in this domain, 1 is interpreted as the identity matrix and A^-1 would give the inverse of the matrix A, if it exists.

Several operations can have the same name, and the types of both the arguments and the result are used to determine which operation is applied (cf. function overloading).

Axiom comes with an extension language called SPAD. All the mathematical knowledge of Axiom is written in this language. The interpreter accepts roughly the same language.

Features[edit]

Within the interpreter environment, Axiom uses type inference and a heuristic algorithm to make explicit type annotations mostly unnecessary.

It features 'HyperDoc', an interactive browser-like help system, and can display two and three dimensional graphics, also providing interactive features like rotation and lighting. It also has a specialized interaction mode for Emacs, as well as a plugin for the TeXmacs editor.

  • HyperDoc displaying the available operations for a domain
    HyperDoc displaying the available operations for a domain
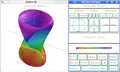
  • Axiom displaying a surface
    Axiom displaying a surface
  • Axiom Firefox Browser Interface
    Axiom Firefox Browser Interface
  • Axiom simplifying a heat equation
    Axiom simplifying a heat equation
  • Axiom matrix manipulation
    Axiom matrix manipulation
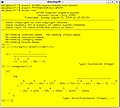
  • Axiom computing a Risch integral
    Axiom computing a Risch integral

Axiom has an implementation of the Risch algorithm for elementary integration, which was done by Manuel Bronstein and Barry Trager. While this implementation can find most elementary antiderivatives and whether they exist, it does have some non-implemented branches, and raises an error when such cases are encountered during integration.[9][10]

See also[edit]

References[edit]

  1. ^ "daly/axiom Tags". Docker Hub. Retrieved 25 March 2022.
  2. ^ Fitch, John (July 23, 2012). "James Griesmer 1929--2011". ACM Communications in Computer Algebra. 46 (1/2): 10–11. doi:10.1145/2338496.2338499. S2CID 36788754.
  3. ^ "Axiom Computer Algebra System". axiom-developer.org.
  4. ^ "Richard D. Jenks Biographical Information". www.eecis.udel.edu.
  5. ^ "EUROCAL '85 | SpringerLink". www.springer.com.
  6. ^ "OpenAxiom: The Open Scientific Computation Platform". www.open-axiom.org.
  7. ^ "FriCAS 18a5ef5d99c796a89efeac06df40043a85b3d44d — FriCAS". fricas.github.io.
  8. ^ "History — FriCAS". fricas.github.io.
  9. ^ Bronstein, Manuel (September 5, 2003). "Manuel Bronstein on Axiom's Integration Capabilities". groups.google.com. Retrieved 2023-02-10.
  10. ^ "integration - Does there exist a complete implementation of the Risch algorithm?". MathOverflow. Oct 15, 2020. Retrieved 2023-02-10.

Further reading[edit]

  • James H. Griesmer; Richard D. Jenks (1971). "SCRATCHPAD/1: An interactive facility for symbolic mathematics | Proceedings of the second ACM symposium on Symbolic and algebraic manipulation (SYMSAC '71)": 42–58. {{cite journal}}: Cite journal requires |journal= (help)
  • Richard D. Jenks (1971). META/PLUS - The Syntax Extension Facility for SCRATCHPAD (Research report). IBM Thomas J. Watson Research Center. RC 3259.
  • James H. Griesmer; Richard D. Jenks (1972). "Experience with an online symbolic mathematics system | Proceedings of the ONLINE72 Conference". 1. Brunel University: 457–476. {{cite journal}}: Cite journal requires |journal= (help)
  • James H. Griesmer; Richard D. Jenks (1972). "Scratchpad". ACM SIGPLAN Notices. 7 (10): 93–102. doi:10.1145/942576.807019.
  • Richard D. Jenks (1974). "The SCRATCHPAD language". ACM SIGSAM Bulletin. 8 (2): 20–30. doi:10.1145/1086830.1086834. S2CID 14537956.
  • Arthur C. Norman (1975). "Computing with Formal Power Series". ACM Transactions on Mathematical Software. 1 (4): 346–356. doi:10.1145/355656.355660. ISSN 0098-3500. S2CID 18321863.
  • Richard D. Jenks (1976). "A pattern compiler | Proceedings of the third ACM symposium on Symbolic and algebraic manipulation (SYMSAC '76)": 60–65. {{cite journal}}: Cite journal requires |journal= (help)
  • E. Lueken (1977). Ueberlegungen zur Implementierung eines Formelmanipulationssystems (Masters thesis) (in German). Germany: Technischen Universitat Carolo-Wilhelmina zu Braunschweig.
  • George E. Andrews (1984). "Ramanujan and SCRATCHPAD | Proceedings of the 1984 MACSYMA Users' Conference". Schenectady: General Electric: 383–408. {{cite journal}}: Cite journal requires |journal= (help)
  • James H. Davenport; P. Gianni; Richard D. Jenks; V. Miller; Scott Morrison; M. Rothstein; C. Sundaresan; Robert S. Sutor; Barry Trager (1984). "Scratchpad". Mathematical Sciences Department, IBM Thomas J. Watson Research Center. {{cite journal}}: Cite journal requires |journal= (help)
  • Richard D. Jenks (1984). "The New SCRATCHPAD Language and System for Computer Algebra". Proceedings of the 1984 MACSYMA Users' Conference: 409–416.
  • Richard D. Jenks (1984). "A primer: 11 keys to New Scratchpad | Proceedings of International Symposium on Symbolic and Algebraic Computation '84". Springer: 123–147. {{cite journal}}: Cite journal requires |journal= (help)
  • Robert S. Sutor (1985). "The Scratchpad II Computer Algebra Language and System | Proceedings of International Symposium on Symbolic and Algebraic Computation '85". Springer: 32–33. {{cite journal}}: Cite journal requires |journal= (help)
  • Rüdiger Gebauer; H. Michael Möller (1986). Buchberger's algorithm and staggered linear bases | Proceedings of the fifth ACM symposium on Symbolic and algebraic computation (International Symposium on Symbolic and Algebraic Computation '86). ACM. pp. 218–221. ISBN 978-0-89791-199-3.
  • Richard D. Jenks; Robert S. Sutor; Stephen M. Watt (1986). Scratchpad II: an abstract datatype system for mathematical computation (Research report). IBM Thomas J. Watson Research Center. RC 12327.
  • Michael Lucks; Bruce W. Char (1986). A fast implementation of polynomial factorization | Proceedings of SYMSAC '86. ACM. pp. 228–232. ISBN 978-0-89791-199-3.
  • J. Purtilo (1986). Applications of a software interconnection system in mathematical problem solving environments | Proceedings of SYMSAC '86. ACM. pp. 16–23. ISBN 978-0-89791-199-3.
  • William H. Burge; Stephen M. Watt (1987). Infinite Structure in SCRATCHPAD II (Research report). IBM Thomas J. Watson Research Center. RC 12794.
  • Pascale Sénéchaud; Françoise Siebert; Gilles Villard (1987). Scratchpad II: Présentation d'un nouveau langage de calcul formel. TIM (Research report) (in French). IMAG, Grenoble Institute of Technology. 640-M.
  • Robert S. Sutor; Richard D. Jenks (1987). "The type inference and coercion facilities in the scratchpad II interpreter". Papers of the Symposium on Interpreters and interpretive techniques - SIGPLAN '87. pp. 56–63. doi:10.1145/29650.29656. ISBN 978-0-89791-235-8. S2CID 17700911.
  • George E. Andrews (1988). R. Janssen (ed.). Application of SCRATCHPAD to problems in special functions and combinatorics | Trends in Computer Algebra. Lecture Notes in Computer Science. Springer. pp. 159–166.
  • James H. Davenport; Yvon Siret; Evelyne Tournier (1993) [1988]. Computer Algebra: Systems and Algorithms for Algebraic Computation. Academic Press. ISBN 978-0122042300.
  • Rüdiger Gebauer; H. Michael Möller (1988). "On an installation of Buchberger's algorithm". Journal of Symbolic Computation. 6 (2–3): 275–286. doi:10.1016/s0747-7171(88)80048-8. ISSN 0747-7171.
  • Fritz Schwarz (1988). R. Janssen (ed.). Programming with abstract data types: the symmetry package (SPDE) in Scratchpad | Trends in Computer Algebra. Lecture Notes in Computer Science. Springer. pp. 167–176.
  • David Shannon; Moss Sweedler (1988). "Using Gröbner bases to determine algebra membership, split surjective algebra homomorphisms determine birational equivalence". Journal of Symbolic Computation. 6 (2–3): 267–273. doi:10.1016/s0747-7171(88)80047-6.
  • Hans-J. Boehm (1989). "Type inference in the presence of type abstraction". ACM SIGPLAN Notices. 24 (7): 192–206. doi:10.1145/74818.74835.
  • Manuel Bronstein (1989). "Simplification of real elementary functions | Proceedings of the International Symposium on Symbolic and Algebraic Computation (SIGSAM '89)". ACM: 207–211. {{cite journal}}: Cite journal requires |journal= (help)
  • Claire Dicrescenzo; Dominique Duval (1989). P. Gianni (ed.). "Algebraic extensions and algebraic closure in Scratchpad II | Symbolic and Algebraic Computation". Springer: 440–446. {{cite journal}}: Cite journal requires |journal= (help)
  • Timothy Daly "Axiom -- Thirty Years of Lisp"
  • Timothy Daly "Axiom" Invited Talk, Free Software Conference, Lyon, France, May, 2002
  • Timothy Daly "Axiom" Invited Talk, Libre Software Meeting, Metz, France, July 9–12, 2003

External links[edit]

Media related to Axiom (computer algebra software) at Wikimedia Commons

Software forks:

Retrieved from "https://en.wikipedia.org/w/index.php?title=Axiom_(computer_algebra_system)&oldid=1213286639"