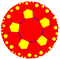
Truncated order-4 pentagonal tiling
| Truncated pentagonal tiling | |
|---|---|
 Poincaré disk model of the hyperbolic plane | |
| Type | Hyperbolic uniform tiling |
| Vertex configuration | 4.10.10 |
| Schläfli symbol | t{5,4} |
| Wythoff symbol | 2 4 | 5 2 5 5 | |
| Coxeter diagram |     or  
|
| Symmetry group | [5,4], (*542) [5,5], (*552) |
| Dual | Order-5 tetrakis square tiling |
| Properties | Vertex-transitive |
In geometry, the truncated order-4 pentagonal tiling is a uniform tiling of the hyperbolic plane. It has Schläfli symbol of t0,1{5,4}.
Uniform colorings
[edit]A half symmetry [1+,4,5] = [5,5] coloring can be constructed with two colors of decagons. This coloring is called a truncated pentapentagonal tiling.
Symmetry
[edit]There is only one subgroup of [5,5], [5,5]+, removing all the mirrors. This symmetry can be doubled to 542 symmetry by adding a bisecting mirror.
| Type | Reflective domains | Rotational symmetry |
|---|---|---|
| Index | 1 | 2 |
| Diagram | 
|
|
| Coxeter (orbifold) |
[5,5] =  =   (*552) |
[5,5]+ =  =  (552) |
Related polyhedra and tiling
[edit]| *n42 symmetry mutation of truncated tilings: 4.2n.2n |
|---|
| Uniform pentagonal/square tilings |
|---|
| Uniform pentapentagonal tilings |
|---|
References
[edit]- John H. Conway, Heidi Burgiel, Chaim Goodman-Strauss, The Symmetries of Things 2008, ISBN 978-1-56881-220-5 (Chapter 19, The Hyperbolic Archimedean Tessellations)
- "Chapter 10: Regular honeycombs in hyperbolic space". The Beauty of Geometry: Twelve Essays. Dover Publications. 1999. ISBN 0-486-40919-8. LCCN 99035678.
See also
[edit]
Wikimedia Commons has media related to Uniform tiling 4-10-10.
External links
[edit]- Weisstein, Eric W. "Hyperbolic tiling". MathWorld.
- Weisstein, Eric W. "Poincaré hyperbolic disk". MathWorld.
- Hyperbolic and Spherical Tiling Gallery
- KaleidoTile 3: Educational software to create spherical, planar and hyperbolic tilings
- Hyperbolic Planar Tessellations, Don Hatch
 | This hyperbolic geometry-related article is a stub. You can help Wikipedia by expanding it. |