Order-4 square hosohedral honeycomb
| Order-4 square hosohedral honeycomb | |
|---|---|
 Centrally projected onto a sphere | |
| Type | Degenerate regular honeycomb |
| Schläfli symbol | {2,4,4} |
| Coxeter diagrams |     
|
| Cells | {2,4} 
|
| Faces | {2} |
| Edge figure | {4} |
| Vertex figure | {4,4}
|
| Dual | Order-2 square tiling honeycomb |
| Coxeter group | [2,4,4] |
| Properties | Regular |
In geometry, the order-4 square hosohedral honeycomb is a regular space-filling tessellation (or honeycomb) with Schläfli symbol {2,4,4}. It has 4 square hosohedra {2,4} around each edge. In other words, it is a packing of infinitely tall square columns. It is a degenerate honeycomb in Euclidean space, but can be seen as a projection onto the sphere. Its vertex figure, a square tiling is seen on each hemisphere.
Images
[edit]Stereographic projections of spherical projection, with all edges being projected into circles.
 Centered on pole |
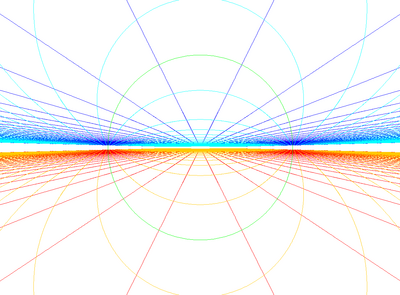 Centered on equator |
Related honeycombs
[edit]It is a part of a sequence of honeycombs with a square tiling vertex figure:
| {p,4,4} honeycombs | ||||||
|---|---|---|---|---|---|---|
| Space | E3 | H3 | ||||
| Form | Affine | Paracompact | Noncompact | |||
| Name | {2,4,4} | {3,4,4} | {4,4,4} | {5,4,4} | {6,4,4} | ..{∞,4,4} |
Coxeter 
|
   
|
  
|
|
  |
  
|
 
|
| Image |
|
|
|
|
|
|
| Cells | {2,4}
|
 {3,4}
|
{4,4}
|
 {5,4}
|
 {6,4}
|
 {∞,4}
|
Truncated order-4 square hosohedral honeycomb
[edit]| Order-2 square tiling honeycomb Truncated order-4 square hosohedral honeycomb 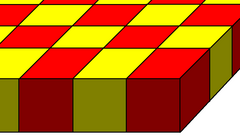 Partial tessellation with alternately colored cubes | |
|---|---|
| Type | uniform convex honeycomb |
| Schläfli symbol | {4,4}×{} |
| Coxeter diagrams |
|
| Cells | {3,4} 
|
| Faces | {4} |
| Vertex figure | Square pyramid |
| Dual | |
| Coxeter group | [2,4,4] |
| Properties | Uniform |
The {2,4,4} honeycomb can be truncated as t{2,4,4} or {}×{4,4}, Coxeter diagram , seen as a layer of cubes, partially shown here with alternately colored cubic cells. Thorold Gosset identified this semiregular infinite honeycomb as a cubic semicheck.
The alternation of this honeycomb, 
, consists of infinite square pyramids and infinite tetrahedrons, between 2 square tilings.
See also
[edit]References
[edit]- The Beauty of Geometry: Twelve Essays (1999), Dover Publications, LCCN 99-35678, ISBN 0-486-40919-8 (Chapter 10, Regular Honeycombs in Hyperbolic Space)