Contact resistance

Electrical contact resistance (ECR, or simply contact resistance) is resistance to the flow of electric current caused by incomplete contact of the surfaces through which the current is flowing, and by films or oxide layers on the contacting surfaces. It occurs at electrical connections such as switches, connectors, breakers, contacts, and measurement probes. Contact resistance values are typically small (in the microohm to milliohm range).

Contact resistance can cause significant voltage drops and heating in circuits with high current. Because contact resistance adds to the intrinsic resistance of the conductors, it can cause significant measurement errors when exact resistance values are needed.

Contact resistance may vary with temperature. It may also vary with time (most often decreasing) in a process known as resistance creep.

Electrical contact resistance is also called interface resistance, transitional resistance, or the correction term. Parasitic resistance is a more general term, of which it is usually assumed that contact resistance is a major component.

William Shockley^[1] introduced the idea of a potential drop on an injection electrode to explain the difference between experimental results and the model of gradual channel approximation.

Measurement methods

Because contact resistance is usually comparatively small, it can difficult to measure, and four-terminal measurement gives better results than a simple two-terminal measurement made with an ohmmeter.

In a two-terminal measurement (as with a typical ohmmeter), the current used to make the measurement is injected through the measurement leads, which causes a potential drop not just across the contact area to be measured but also across the probe contacts and the leads. That means that the contact resistance of the probes and their leads is inseparable from the resistance of the contact area to be measured, with which they are in series.
In a four-terminal measurement, the current used to make the measurement is injected using a second, separate pair of leads, so the contact resistance of the measurement probes and their leads is not included in the measurement.

Specific contact resistance can be obtained by multiplying by contact area.

Experimental characterization

For experimental characterization, a distinction must be made between contact resistance evaluation in two-electrode systems (for example, diodes) and three-electrode systems (for example, transistors).

In two-electrode systems, specific contact resistivity is experimentally defined as the slope of the I–V curve at V = 0:

r_{\text{c}}=\left\{{\frac {\partial V}{\partial J}}\right\}_{V=0}

where $J$ is the current density, or current per area. The units of specific contact resistivity are typically therefore in ohm-square metre, or Ω⋅m². When the current is a linear function of the voltage, the device is said to have ohmic contacts. Inductive and capacitive methods could be used in principle to measure an intrinsic impedance without the complication of contact resistance. In practice, direct current methods are more typically used to determine resistance.

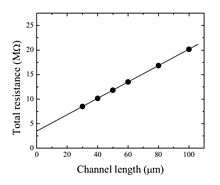
The three electrode systems such as transistors require more complicated methods for the contact resistance approximation. The most common approach is the transmission line model (TLM). Here, the total device resistance $R_{\text{tot}}$ is plotted as a function of the channel length:

R_{\text{tot}}=R_{\text{c}}+R_{\text{ch}}=R_{\text{c}}+{\frac {L}{WC\mu \left(V_{\text{gs}}-V_{\text{ds}}\right)}}

where $R_{\text{c}}$ and $R_{\text{ch}}$ are contact and channel resistances, respectively, $L/W$ is the channel length/width, $C$ is gate insulator capacitance (per unit of area), $\mu$ is carrier mobility, and $V_{\text{gs}}$ and $V_{\text{ds}}$ are gate-source and drain-source voltages. Therefore, the linear extrapolation of total resistance to the zero channel length provides the contact resistance. The slope of the linear function is related to the channel transconductance and can be used for estimation of the ”contact resistance-free” carrier mobility. The approximations used here (linear potential drop across the channel region, constant contact resistance, ...) lead sometimes to the channel dependent contact resistance.^[2]

Beside the TLM it was proposed the gated four-probe measurement^[3] and the modified time-of-flight method (TOF).^[4] The direct methods able to measure potential drop on the injection electrode directly are the Kelvin probe force microscopy (KFM)^[5] and the electric-field induced second harmonic generation.^[6]

In the semiconductor industry, Cross-Bridge Kelvin Resistor(CBKR) structures are the mostly used test structures to characterize metal-semiconductor contacts in the Planar devices of VLSI technology. During the measurement process, force the current ( $I$ ) between contacts 1 and 2 and measure the potential deference between contacts 3 and 4. The contact resistance $R_{\text{k}}$ can be then calculated as $R_{\text{k}}=V_{34}/I$ .^[7]

Mechanisms

For given physical and mechanical material properties, parameters that govern the magnitude of electrical contact resistance (ECR) and its variation at an interface relate primarily to surface structure and applied load (Contact mechanics).^[8] Surfaces of metallic contacts generally exhibit an external layer of oxide material and adsorbed water molecules, which lead to capacitor-type junctions at weakly contacting asperities and resistor type contacts at strongly contacting asperities, where sufficient pressure is applied for asperities to penetrate the oxide layer, forming metal-to-metal contact patches. If a contact patch is sufficiently small, with dimensions comparable or smaller than the mean free path of electrons resistance at the patch can be described by the Sharvin mechanism, whereby electron transport can be described by ballistic conduction. Generally, over time, contact patches expand and the contact resistance at an interface relaxes, particularly at weakly contacting surfaces, through current induced welding and dielectric breakdown. This process is known also as resistance creep.^[9] The coupling of surface chemistry, contact mechanics and charge transport mechanisms needs to be considered in the mechanistic evaluation of ECR phenomena.

Quantum limit

When a conductor has spatial dimensions close to $2\pi /k_{\text{F}}$ , where $k_{\text{F}}$ is Fermi wavevector of the conducting material, Ohm's law does not hold anymore. These small devices are called quantum point contacts. Their conductance must be an integer multiple of the value $2e^{2}/h$ , where $e$ is the elementary charge and $h$ is the Planck constant. Quantum point contacts behave more like waveguides than the classical wires of everyday life and may be described by the Landauer scattering formalism.^[10] Point-contact tunneling is an important technique for characterizing superconductors.

Other forms of contact resistance

Measurements of thermal conductivity are also subject to contact resistance, with particular significance in heat transport through granular media. Similarly, a drop in hydrostatic pressure (analogous to electrical voltage) occurs when fluid flow transitions from one channel to another.

Significance

Bad contacts are the cause of failure or poor performance in a wide variety of electrical devices. For example, corroded jumper cable clamps can frustrate attempts to start a vehicle that has a low battery. Dirty or corroded contacts on a fuse or its holder can give the false impression that the fuse is blown. A sufficiently high contact resistance can cause substantial heating in a high current device. Unpredictable or noisy contacts are a major cause of the failure of electrical equipment.

References

^ Shockley, William (September 1964). "Research and investigation of inverse epitaxial UHF power transistors". Report No. A1-TOR-64-207. {{cite journal}}: Cite journal requires |journal= (help)
^ Weis, Martin; Lin, Jack; Taguchi, Dai; Manaka, Takaaki; Iwamoto, Mitsumasa (2010). "Insight into the contact resistance problem by direct probing of the potential drop in organic field-effect transistors". Applied Physics Letters. 97 (26): 263304. Bibcode:2010ApPhL..97z3304W. doi:10.1063/1.3533020.
^ Pesavento, Paul V.; Chesterfield, Reid J.; Newman, Christopher R.; Frisbie, C. Daniel (2004). "Gated four-probe measurements on pentacene thin-film transistors: Contact resistance as a function of gate voltage and temperature". Journal of Applied Physics. 96 (12): 7312. Bibcode:2004JAP....96.7312P. doi:10.1063/1.1806533.
^ Weis, Martin; Lin, Jack; Taguchi, Dai; Manaka, Takaaki; Iwamoto, Mitsumasa (2009). "Analysis of Transient Currents in Organic Field Effect Transistor: The Time-of-Flight Method". Journal of Physical Chemistry C. 113 (43): 18459. doi:10.1021/jp908381b.
^ Bürgi, L.; Sirringhaus, H.; Friend, R. H. (2002). "Noncontact potentiometry of polymer field-effect transistors". Applied Physics Letters. 80 (16): 2913. Bibcode:2002ApPhL..80.2913B. doi:10.1063/1.1470702.
^ Nakao, Motoharu; Manaka, Takaaki; Weis, Martin; Lim, Eunju; Iwamoto, Mitsumasa (2009). "Probing carrier injection into pentacene field effect transistor by time-resolved microscopic optical second harmonic generation measurement". Journal of Applied Physics. 106 (1): 014511–014511–5. Bibcode:2009JAP...106a4511N. doi:10.1063/1.3168434.
^ Stavitski, Natalie; Klootwijk, Johan H.; van Zeijl, Henk W.; Kovalgin, Alexey Y.; Wolters, Rob A. M. (February 2009). "Cross-Bridge Kelvin Resistor Structures for Reliable Measurement of Low Contact Resistances and Contact Interface Characterization". IEEE Transactions on Semiconductor Manufacturing. 22 (1): 146–152. doi:10.1109/TSM.2008.2010746. ISSN 0894-6507. S2CID 111829.
^ Zhai, Chongpu; Hanaor, Dorian; Proust, Gwénaëlle; Brassart, Laurence; Gan, Yixiang (December 2016). "Interfacial electro-mechanical behaviour at rough surfaces" (PDF). Extreme Mechanics Letters. 9 (3): 422–429. Bibcode:2016ExML....9..422Z. doi:10.1016/j.eml.2016.03.021. hdl:1959.4/unsworks_60452.
^ Zhai, Chongpu; Hanaor, Dorian A. H.; Proust, Gwenaelle; Gan, Yixiang (2015). "Stress-Dependent Electrical Contact Resistance at Fractal Rough Surfaces". Journal of Engineering Mechanics. 143 (3): B4015001. doi:10.1061/(ASCE)EM.1943-7889.0000967.
^ Landauer, Rolf (August 1976). "Spatial carrier density modulation effects in metallic conductivity". Physical Review B. 14 (4): 1474–1479. Bibcode:1976PhRvB..14.1474L. doi:10.1103/PhysRevB.14.1474.