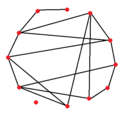
Сеть маленького мира
Хабы больше, чем другие узлы
Средняя степень = 2,833
Средняя длина кратчайшего пути = 2,109.
Коэффициент кластеризации = 0,167
| Часть серии о | ||||
| Сетевая наука | ||||
|---|---|---|---|---|
| Типы сетей | ||||
| Графики | ||||
| ||||
| Модели | ||||
| ||||
| ||||
Сеть маленького мира — это граф, характеризующийся высоким коэффициентом кластеризации и малыми расстояниями . На примере социальной сети высокая кластеризация подразумевает высокую вероятность того, что двое друзей одного человека сами являются друзьями. С другой стороны, небольшие расстояния означают, что между любыми двумя людьми существует короткая цепочка социальных связей (этот эффект известен как шесть степеней разделения ). [1] В частности, сеть маленького мира определяется как сеть, в которой типичное расстояние L между двумя случайно выбранными узлами (количество необходимых шагов) растет пропорционально логарифму количества узлов N в сети, то есть: [2]
в то время как глобальный коэффициент кластеризации не мал.
В контексте социальной сети это приводит к феномену маленького мира , когда незнакомцы связаны короткой цепочкой знакомств . Многие эмпирические графики демонстрируют эффект тесного мира, включая социальные сети , вики, такие как Arc.Ask3.Ru, генные сети и даже лежащую в основе архитектуру Интернета . Это вдохновение для многих сетевых архитектур в современном компьютерном оборудовании . [3]
как класс случайных графов Определенная категория сетей маленького мира была определена Дунканом Уоттсом и Стивеном Строгацем в 1998 году. [4] Они отметили, что графы можно классифицировать по двум независимым структурным характеристикам, а именно по коэффициенту кластеризации между узлами и среднему расстоянию (также известному как средняя длина кратчайшего пути ). Чисто случайные графы, построенные в соответствии с моделью Эрдеша-Реньи (ER) , демонстрируют небольшую среднюю длину кратчайшего пути (обычно варьирующуюся как логарифм количества узлов) наряду с небольшим коэффициентом кластеризации. Уоттс и Строгац подсчитали, что на самом деле многие реальные сети имеют небольшую среднюю длину кратчайшего пути, но при этом коэффициент кластеризации значительно выше, чем ожидалось по случайности. Затем Уоттс и Строгац предложили новую графовую модель, в настоящее время называемую моделью Уоттса и Строгаца , с (i) небольшой средней длиной кратчайшего пути и (ii) большим коэффициентом кластеризации. Переход в модели Уоттса-Строгаца между «большим миром» (таким как решетка) и маленьким миром был впервые описан Бартелеми и Амаралом в 1999 году. [5] За этой работой последовало множество исследований, в том числе с точными результатами (Баррат и Вейгт, 1999; Дороговцев и Мендес ; Бармпутис и Мюррей, 2010).
Свойства сетей маленького мира
[ редактировать ]Сети маленького мира, как правило, содержат клики и почти клики, то есть подсети, которые имеют связи практически между любыми двумя узлами внутри них. Это следует из определяющего свойства высокого коэффициента кластеризации . Во-вторых, большинство пар узлов будут соединены хотя бы одним коротким путем. Это следует из определяющего свойства: средняя длина кратчайшего пути мала. Некоторые другие свойства часто связаны с сетями маленького мира. Обычно наблюдается избыток концентраторов — узлов в сети с большим количеством соединений (известных как узлы высокой степени ). Эти концентраторы служат общими соединениями, обеспечивающими короткие пути между другими ребрами. По аналогии, сеть авиарейсов маленького мира имеет небольшую среднюю длину пути (т. е. между любыми двумя городами вам, скорее всего, придется совершить три или меньше рейсов), поскольку многие рейсы направляются через центральные города. Это свойство часто анализируется путем рассмотрения доли узлов в сети, к которым имеется определенное количество входящих в них соединений (степень распределения сети). Сети с большим, чем ожидалось, количеством концентраторов будут иметь большую долю узлов с высокой степенью, и, следовательно, распределение степеней будет обогащено при высоких значениях степени. В просторечии это известно как распределение с толстым хвостом . Графы с очень разной топологией квалифицируются как сети малого мира, если они удовлетворяют двум приведенным выше определяющим требованиям.
Тесность сетевого мира количественно оценивается с помощью коэффициента малого , рассчитанный путем сравнения кластеризации и длины пути данной сети с моделью Эрдеша – Реньи в среднем с той же степенью. [6] [7]
- если ( и ), сеть — это маленький мир. Однако известно, что этот показатель работает плохо, поскольку на него сильно влияет размер сети. [8] [9]
Другой метод количественной оценки тесноты сети использует исходное определение сети малого мира, сравнивая кластеризацию данной сети с эквивалентной решетчатой сетью и длину ее пути с эквивалентной случайной сетью. Мера маленького мира ( ) определяется как [8]
Если характерная длина пути L и коэффициент кластеризации C рассчитываются на основе тестируемой сети, C ℓ — это коэффициент кластеризации для эквивалентной решетчатой сети, а L r — характерная длина пути для эквивалентной случайной сети.
Еще один метод количественной оценки тесноты мира нормализует как кластеризацию сети, так и длину пути относительно этих характеристик в эквивалентной решетке и случайных сетях. Индекс маленького мира (SWI) определяется как [9]
И ω ′, и SWI находятся в диапазоне от 0 до 1 и, как было показано, отражают аспекты тесноты мира. Однако они придерживаются несколько разных концепций идеального маленького мира. Для данного набора ограничений (например, размера, плотности, распределения степеней) существует сеть, для которой ω ′ = 1, и, таким образом , ω стремится охватить степень, в которой сеть с заданными ограничениями является настолько маленькой, насколько это возможно. Напротив, может не существовать сети, для которой SWI = 1, поэтому SWI стремится определить степень, в которой сеть с заданными ограничениями приближается к теоретическому идеальному маленькому миру сети, где C ≈ C ℓ и L ≈ L r . [9]
Примеры сетей маленького мира
[ редактировать ]Свойства маленького мира обнаруживаются во многих явлениях реального мира, включая веб-сайты с навигационными меню, пищевые сети, электрические сети, сети обработки метаболитов, сети нейронов головного мозга . сети избирателей, графики телефонных звонков и сети аэропортов. [10] Культурные сети [11] и сети совпадения слов [12] также было показано, что это сети маленького мира.
Сети связанных белков обладают свойствами маленького мира, такими как степенное распределение степеней. [13] Точно так же транскрипционные сети , в которых узлами являются гены , и они связаны, если один ген оказывает положительное или отрицательное регулирующее генетическое влияние на другой, обладают свойствами небольшой мировой сети. [14]
Примеры сетей немаленького мира
[ редактировать ]Другой пример: знаменитая теория « шести степеней разделения » между людьми молчаливо предполагает, что областью дискурса является совокупность людей, живущих в любой момент времени. Число степеней разделения между Альбертом Эйнштейном и Александром Великим почти наверняка превышает 30. [15] и эта сеть не обладает свойствами маленького мира. Аналогично ограниченной сетью может быть сеть «ходили в школу вместе»: если два человека учились в одном и том же колледже с разницей в десять лет, маловероятно, что у них есть общие знакомые среди студентов.
Точно так же количество ретрансляционных станций, через которые должно пройти сообщение, не всегда было небольшим. В те дни, когда почту доставляли вручную или верхом на лошади, количество раз, когда письмо переходило из рук в руки от источника к месту назначения, было бы намного больше, чем сегодня. Количество раз, когда сообщение переходило из рук в руки во времена визуального телеграфа (около 1800–1850 гг.), определялось требованием, чтобы две станции были соединены прямой видимостью.
Неявные предположения, если их не изучить, могут вызвать предвзятость в литературе по графам в пользу поиска сетей маленького мира (пример эффекта ящика с файлами, возникающего из-за предвзятости публикации ).
Надежность сети
[ редактировать ], предполагают Некоторые исследователи, такие как Альберт-Ласло Барабаши , что преобладание малых мировых сетей в биологических системах может отражать эволюционное преимущество такой архитектуры. Одна из возможностей заключается в том, что сети маленького мира более устойчивы к возмущениям, чем другие сетевые архитектуры. Если бы это было так, это дало бы преимущество биологическим системам, которые подвержены повреждениям в результате мутаций или вирусной инфекции .
В небольшой мировой сети со степенным распределением степеней удаление случайного узла редко приводит к резкому увеличению средней длины кратчайшего пути (или резкому уменьшению коэффициента кластеризации ). Это следует из того, что большинство кратчайших путей между узлами проходят через хабы , и удаление периферийного узла вряд ли будет мешать проходу между другими периферийными узлами. Поскольку доля периферийных узлов в маленькой мировой сети намного превышает долю хабов , вероятность удаления важного узла очень мала. Например, если бы небольшой аэропорт в Сан-Вэлли, штат Айдахо , был закрыт, это не увеличило бы среднее количество рейсов, которые другим пассажирам, путешествующим по Соединенным Штатам, пришлось бы совершать, чтобы добраться до соответствующих пунктов назначения. Однако если случайное удаление узла случайно затронет концентратор, средняя длина пути может значительно увеличиться. Это можно наблюдать ежегодно, когда северные узловые аэропорты, такие как Чикаго, Аэропорт О'Хара закрыт из-за снега; многим людям приходится совершать дополнительные рейсы.
Напротив, в случайной сети, в которой все узлы имеют примерно одинаковое количество соединений, удаление случайного узла, вероятно, немного, но значительно увеличит среднюю длину кратчайшего пути практически для любого удаленного узла. В этом смысле случайные сети уязвимы к случайным возмущениям, тогда как сети малого мира устойчивы. Однако сети малого мира уязвимы для целенаправленных атак на концентраторы, тогда как случайные сети не могут стать целью катастрофического сбоя.
Строительство сетей маленького мира
[ редактировать ]Основным механизмом построения сетей маленького мира является механизм Уоттса-Строгаца .
Сети малого мира также могут быть внедрены с задержкой по времени, [16] который создаст не только фракталы, но и хаос [17] при правильных условиях или переход к хаосу в динамических сетях. [18]
Вскоре после публикации механизма Уоттса-Строгаца и его коллеги разработали подходы Машаги для создания сетевых моделей, которые демонстрируют корреляции высокой степени, сохраняя при этом желаемое распределение степеней и свойства маленького мира. Эти подходы основаны на двойственном преобразовании и могут использоваться для создания аналитически решаемых сетевых моделей маленького мира для исследования этих систем. [19]
Графы степень-диаметр строятся так, что число соседей каждой вершины в сети ограничено, а расстояние от любой данной вершины в сети до любой другой вершины (диаметр сети ) минимизировано. Построение таких сетей маленького мира осуществляется в рамках усилий по поиску графов порядка, близких к границе Мура .
Другой способ построить небольшую всемирную сеть с нуля представлен в Barmpoutis et al. , [20] где построена сеть с очень маленьким средним расстоянием и очень большой средней кластеризацией. Приведен быстрый алгоритм постоянной сложности, а также измерения устойчивости полученных графов. В зависимости от применения каждой сети можно начать с одной такой сети «сверхмалого мира», а затем пересоединить некоторые ребра или использовать несколько небольших таких сетей в качестве подграфов к более крупному графу.
Свойства маленького мира могут естественным образом возникнуть в социальных сетях и других системах реального мира в процессе двухфазной эволюции . Это особенно распространено там, где временные или пространственные ограничения ограничивают добавление связей между вершинами. Механизм обычно включает периодические сдвиги между фазами, при этом соединения добавляются во время «глобальной» фазы и усиливаются или удаляются во время «локальной» фазы.
Сети маленького мира могут перейти от безмасштабного класса к широкомасштабному классу, распределение связности которого имеет резкое ограничение в соответствии со степенным законом из-за ограничений, ограничивающих добавление новых каналов. [21] При достаточно сильных ограничениях безмасштабные сети могут даже стать одномасштабными сетями, распределение связности которых характеризуется как быстро затухающее. [21] Аналитически было также показано, что безмасштабные сети очень малы, а это означает, что расстояние масштабируется в соответствии с . [22]
Приложения
[ редактировать ]Приложения к социологии
[ редактировать ]Преимущества небольших мировых сетей для групп социальных движений заключаются в их устойчивости к изменениям благодаря фильтрующему аппарату с использованием узлов с высокой степенью связи, а также в более высокой эффективности передачи информации при сохранении минимального количества ссылок, необходимых для подключения к сети. [23]
Модель сети маленького мира напрямую применима к теории аффинити-групп, представленной в социологических аргументах Уильямом Финнеганом . Группы по интересам — это небольшие и полунезависимые группы социальных движений, приверженные более широкой цели или функции. Хотя они в основном не связаны на уровне узлов, несколько членов с высокой связностью функционируют как узлы связности, связывая различные группы через сеть. Эта модель маленького мира оказалась чрезвычайно эффективной тактикой организации протеста против действий полиции. [24] Клэй Ширки утверждает, что чем крупнее социальная сеть, созданная посредством создания сетей маленького мира, тем более ценными являются узлы с высокой связностью внутри сети. [23] То же самое можно сказать и о модели группы по интересам, где небольшое количество людей внутри каждой группы, связанных с внешними группами, обеспечивает значительную мобилизацию и адаптацию. Практическим примером этого является создание сетей маленького мира через группы по интересам, которые Уильям Финнеган обрисовал в общих чертах в связи с протестами ВТО в Сиэтле в 1999 году .
Приложения к наукам о Земле
[ редактировать ]Было показано, что многие сети, изучаемые в геологии и геофизике, обладают характеристиками сетей маленького мира. Сети, определенные в системах трещин и пористых веществах, продемонстрировали эти характеристики. [25] Сейсмическая сеть в регионе Южной Калифорнии может быть сетью маленького мира. [26] Приведенные выше примеры встречаются в самых разных пространственных масштабах, демонстрируя масштабную инвариантность явления в науках о Земле.
Приложения к вычислениям
[ редактировать ]Сети маленького мира использовались для оценки удобства использования информации, хранящейся в больших базах данных. Эта мера называется «Мера преобразования данных маленького мира». [27] [28] Чем больше ссылки базы данных соответствуют сети маленького мира, тем больше вероятность того, что пользователь сможет извлекать информацию в будущем. Такое удобство использования обычно достигается за счет объема информации, которая может храниться в одном репозитории.
. В симуляции было показано , что одноранговая сеть Freenet образует сеть маленького мира [29] позволяя хранить и извлекать информацию таким образом, чтобы эффективность масштабировалась по мере роста сети.
для поиска ближайших соседей, Решения такие как HNSW, используют сети маленького мира для эффективного поиска информации в больших массивах элементов. [30] [31]
Нейронные сети маленького мира в мозге
[ редактировать ]Обе анатомические связи в мозге [32] и сети синхронизации корковых нейронов [33] продемонстрировать топологию маленького мира.
Также было обнаружено, что структурные и функциональные связи в мозге отражают топологию маленького мира с короткой длиной пути и высокой кластеризацией. [34] Сетевая структура была обнаружена в коре головного мозга млекопитающих у разных видов, а также в ходе крупномасштабных исследований изображений на людях. [35] Достижения в области коннектомики и сетевой нейробиологии показали, что ограниченность нейронных сетей связана с эффективной коммуникацией. [36]
В нейронных сетях короткая длина пути между узлами и высокая кластеризация в сетевых концентраторах обеспечивают эффективную связь между областями мозга при минимальных энергетических затратах. [36] Мозг постоянно обрабатывает и адаптируется к новой информации, а сетевая модель маленького мира поддерживает интенсивные коммуникационные потребности нейронных сетей. [37] Высокая кластеризация узлов образует локальные сети, которые часто функционально связаны. Короткая длина пути между этими концентраторами обеспечивает эффективную глобальную связь. [38] Этот баланс обеспечивает эффективность глобальной сети и одновременно дает возможность мозгу справляться с сбоями и поддерживать гомеостаз благодаря изоляции локальных подсистем от глобальной сети. [39] Было обнаружено, что потеря сетевой структуры маленького мира указывает на изменения в познании и повышенный риск психологических расстройств. [9]
Помимо характеристики функциональной и структурной связи всего мозга, определенные нейронные системы, такие как зрительная система, демонстрируют свойства сети маленького мира. [6]
Небольшая сеть нейронов может обладать кратковременной памятью . Компьютерная модель, разработанная Сарой Соллой. [40] [41] имел два стабильных состояния — свойство (называемое бистабильностью ), которое считалось важным при хранении в памяти . Активирующий импульс генерировал самоподдерживающиеся петли коммуникационной активности между нейронами. Второй импульс положил конец этой деятельности. Импульсы переключали систему между стабильными состояниями: потоком (запись «памяти») и стазисом (удержанием ее). Нейронные сети маленького мира также использовались в качестве моделей для понимания припадков . [42]
См. также
[ редактировать ]- Модель Барабаши – Альберта – Алгоритм создания безмасштабной сети
- Климат как сложная сеть – концептуальная модель для понимания климатологии
- Двухфазная эволюция - процесс, который стимулирует самоорганизацию в сложных адаптивных системах.
- Число Данбара - предлагаемый когнитивный предел, важный в социологии и антропологии.
- Число Эрдеша - близость чьей-либо связи с математиком Полем Эрдешем.
- Модель Эрдеша – Реньи (ER) – две тесно связанные модели для создания случайных графов.
- Развивающиеся сетевые модели локального мира
- Теория перколяции - Математическая теория поведения связанных кластеров в случайном графе.
- Сетевая наука - Академическая область - математическая теория сетей.
- Безмасштабная сеть - сеть, распределение степеней которой подчиняется степенному закону.
- Шесть степеней Кевина Бэкона – Салонная игра о степенях разделения
- Эксперимент маленького мира - эксперименты по изучению средней длины пути в социальных сетях.
- Социальная сеть - социальная структура, состоящая из набора социальных субъектов.
- Модель Уоттса-Строгаца - метод генерации случайных графов маленького мира
- Сеть на кристалле - Подсистема электронной связи на интегральной схеме - системы на кристалле, смоделированные на основе сетей маленького мира.
- клуб каратэ Закари
Ссылки
[ редактировать ]- ^ Дауни, Аллен Б. (2016). «3». Думайте о сложности (PDF) . Нидхэм, Массачусетс: Пресса для зеленого чая . п. 27.
- ^ Уоттс-ди-джей, Строгац С.Х. (июнь 1998 г.). «Коллективная динамика сетей «маленького мира». Природа . 393 (6684): 440–2. Бибкод : 1998Natur.393..440W . дои : 10.1038/30918 . ПМИД 9623998 . S2CID 4429113 .
- ^ Кунду С., Чаттопадхьяй С. (2014). Сеть на кристалле: следующее поколение интеграции системы на кристалле (1-е изд.). Бока-Ратон, Флорида: CRC Press. ISBN 9781466565272 . OCLC 895661009 .
- ^ Уоттс-ди-джей, Строгац С.Х. (июнь 1998 г.). «Коллективная динамика сетей «маленького мира». Природа . 393 (6684): 440–2. Бибкод : 1998Natur.393..440W . дои : 10.1038/30918 . ПМИД 9623998 . S2CID 4429113 .
- ^ Бартелеми М., Амарал Л.А. (1999). «Сети маленького мира: свидетельства перекрестной картины». Письма о физических отзывах . 82 (15): 3180–3183. arXiv : cond-mat/9903108 . Бибкод : 1999PhRvL..82.3180B . дои : 10.1103/PhysRevLett.82.3180 . S2CID 119398712 .
- ^ Перейти обратно: а б Хамфрис, доктор медицины (2006). «Ретикулярная формация ствола мозга представляет собой маленький мир, а не безмасштабную сеть» . Труды Королевского общества B: Биологические науки . 273 (1585): 503–511. дои : 10.1098/rspb.2005.3354 . ПМК 1560205 . ПМИД 16615219 .
- ^ Хамфрис, доктор медицинских наук, Герни К. (апрель 2008 г.). «Малость сети»: количественный метод определения канонической сетевой эквивалентности» . ПЛОС ОДИН . 3 (4): e0002051. Бибкод : 2008PLoSO...3.2051H . дои : 10.1371/journal.pone.0002051 . ПМЦ 2323569 . ПМИД 18446219 .
- ^ Перейти обратно: а б Телесфорд К.К., Джойс К.Е., Хаясака С., Бердетт Дж.Х., Лауриенти П.Дж. (2011). «Повсеместное распространение сетей маленького мира» . Мозговая связь . 1 (5): 367–75. arXiv : 1109.5454 . Бибкод : 2011arXiv1109.5454T . дои : 10.1089/brain.2011.0038 . ПМЦ 3604768 . ПМИД 22432451 .
- ^ Перейти обратно: а б с д Нил ЗП (2017). «Насколько он мал? Сравнивая показатели маломирства». Сетевая наука . 5 (1): 30–44. дои : 10.1017/nws.2017.5 . ISSN 2050-1242 . S2CID 3844585 .
- ^ Ян Ю.К. (1972). «Терминальные автомобильные мосты международного аэропорта Сан-Франциско». Труды журнала ACI . 69 (10). дои : 10.14359/7189 .
- ^ Сенекал Б.А. (декабрь 2015 г.). « Количественная оценка маленьких миров в африканских культурных сетях по сравнению с другими сложными сетями: естественные науки» [Количественная оценка маленьких миров в африканских культурных сетях по сравнению с другими сложными сетями: естественные науки.]. Журнал гуманитарных, естественных, юридических и религиозных наук (на языке африкаанс). 12 (3). Литнет Академический: 665–88.
- ^ Сенекал Б., Коце Э (2017). «Статистические свойства письменности африкаанс как сложной сети». Журнал гуманитарных, естественных, юридических и религиозных наук (на языке африкаанс). 14 (1). Литнет Академический: 27–59.
- ^ Борк П., Йенсен Л.Дж., фон Меринг С., Рамани А.К., Ли И., Маркотт Э.М. (июнь 2004 г.). «Сети взаимодействия белков от дрожжей до человека» (PDF) . Современное мнение в области структурной биологии . 14 (3): 292–9. дои : 10.1016/j.sbi.2004.05.003 . ПМИД 15193308 .
- ^ ван Ноорт В., Снел Б., Хюйнен М.А. (март 2004 г.). «Сеть коэкспрессии дрожжей имеет небольшую, немасштабируемую архитектуру и может быть объяснена простой моделью» . Отчеты ЭМБО . 5 (3): 280–4. дои : 10.1038/sj.embor.7400090 . ПМК 1299002 . ПМИД 14968131 .
- ↑ Эйнштейн и Александр Македонский жили с разницей в 2202 года. Если предположить, что разница в возрасте между любыми двумя людьми в цепочке, соединяющей их, составляет 70 лет, это потребует как минимум 32 связей между Эйнштейном и Александром Великим.
- ^ Ян XS (2002). «Фракталы в сетях маленького мира с задержкой». Хаос, солитоны и фракталы . 13 (2): 215–219. arXiv : 1003.4949 . Бибкод : 2002CSF....13..215Y . дои : 10.1016/S0960-0779(00)00265-4 . S2CID 119109068 .
- ^ Ян XS (март 2001 г.). «Хаос в сетях маленького мира». Физический обзор E . 63 (4): 046206. arXiv : 1003.4940 . Бибкод : 2001PhRvE..63d6206Y . дои : 10.1103/PhysRevE.63.046206 . ПМИД 11308929 . S2CID 38158445 .
- ^ Юань WJ, Луо XS, Цзян PQ, Ван BH, Фан JQ (август 2008 г.). «Переход к хаосу в динамической сети маленького мира». Хаос, солитоны и фракталы . 37 (3): 799–806. Бибкод : 2008CSF....37..799Y . дои : 10.1016/j.chaos.2006.09.077 .
- ^ А. Рамезанпур, В. Каримипур, А. Машаги, Создание коррелированных сетей из некоррелированных. Physical Review E 67(4 Pt 2):046107 (2003) doi: 10.1103/PhysRevE.67.046107
- ^ Бармпутис Д., Мюррей Р.М. (2010). «Сети с наименьшим средним расстоянием и наибольшей средней кластеризацией». arXiv : 1007.4031 [ q-bio.MN ].
- ^ Перейти обратно: а б Амарал Л.А., Скала А., Бартелеми М., Стэнли Х.Э. (октябрь 2000 г.). «Классы сетей маленького мира» . Труды Национальной академии наук Соединенных Штатов Америки . 97 (21): 11149–52. arXiv : cond-mat/0001458 . Бибкод : 2000PNAS...9711149A . дои : 10.1073/pnas.200327197 . ЧВК 17168 . ПМИД 11005838 .
- ^ Коэн Р., Хэвлин С. (2003). «Безмасштабные сети сверхмаленькие» . Письма о физических отзывах . 90 (5): 058701. arXiv : cond-mat/0205476 . Бибкод : 2003PhRvL..90e8701C . doi : 10.1103/PhysRevLett.90.058701 . ПМИД 12633404 . S2CID 10508339 .
- ^ Перейти обратно: а б Ширки С (2008). А вот и все: сила организации без организаций . Пингвин Пресс. ISBN 978-1-59420-153-0 . OCLC 168716646 .
- ^ Финнеган, Уильям «Группы по интересам и движение против корпоративной глобализации»
- ^ Ян XS (июль 2001 г.). «Сети маленького мира в геофизике». Письма о геофизических исследованиях . 28 (13): 2549–52. arXiv : 1003.4886 . Бибкод : 2001GeoRL..28.2549Y . дои : 10.1029/2000GL011898 . S2CID 118655139 . (2001)
- ^ Хименес А., Тиампо К.Ф., Посадас А.М. (май 2008 г.). «Маленький мир в сейсмической сети: случай Калифорнии» (PDF) . Нелинейные процессы в геофизике . 15 (3): 389–95. Бибкод : 2008NPGeo..15..389J . дои : 10.5194/npg-15-389-2008 .
- ^ Хиллард Р., МакКлоури С., Сомич Б. «Мера преобразования данных в маленьких мирах» . MIKE2.0, методология разработки информации с открытым исходным кодом . Архивировано из оригинала 12 сентября 2015 г. Проверено 5 января 2012 г.
- ^ Хиллард Р. (2010). Информационный бизнес . Уайли. ISBN 978-0-470-62577-4 .
- ^ Сандберг О (2005). В поисках в маленьком мире (PDF) (кандидатская диссертация). Гетеборг, Швеция: Технологический университет Чалмерса и Гетеборгский университет. Архивировано (PDF) из оригинала 16 марта 2012 г. Проверено 12 декабря 2013 г.
- ^ «Иерархические навигационные малые миры (HNSW) | Сосновая шишка» . www.pinecone.io . Проверено 5 марта 2024 г.
- ^ «Понимание иерархических навигационных малых миров (HNSW)» . ДатаСтакс . Проверено 5 марта 2024 г.
- ^ Спорнс О, Чиалво Д.Р., Кайзер М., Хильгетаг CC (сентябрь 2004 г.). «Организация, развитие и функции сложных мозговых сетей». Тенденции в когнитивных науках . 8 (9): 418–25. дои : 10.1016/j.tics.2004.07.008 . ПМИД 15350243 . S2CID 2855338 .
- ^ Ю С., Хуан Д., Сингер В., Николич Д. (декабрь 2008 г.). «Маленький мир нейронной синхронизации» . Кора головного мозга . 18 (12): 2891–901. дои : 10.1093/cercor/bhn047 . ПМЦ 2583154 . ПМИД 18400792 .
- ^ Бассетт, Даниэль С.; Буллмор, Эдвард Т. (23 октября 2017 г.). «Возвращение к мозговым сетям маленького мира» . Нейробиолог . 23 (5): 499–516. дои : 10.1177/1073858416667720 . ISSN 1073-8584 . ПМК 5603984 . ПМИД 27655008 .
- ^ Бетанкур, Луис М.А.; Стивенс, Грег Дж.; Хэм, Майкл И.; Гросс, Гюнтер В. (23 февраля 2007 г.). «Функциональная структура корковых нейрональных сетей, выращенных in vitro» . Физический обзор E . 75 (2): 021915. arXiv : q-bio/0703018 . Бибкод : 2007PhRvE..75b1915B . дои : 10.1103/PhysRevE.75.021915 . ISSN 1539-3755 . ПМИД 17358375 . S2CID 14757568 .
- ^ Перейти обратно: а б Буллмор, Эд; Спорнс, Олаф (13 апреля 2012 г.). «Экономика организации мозговых сетей» . Обзоры природы. Нейронаука . 13 (5): 336–349. дои : 10.1038/nrn3214 . ISSN 1471-0048 . ПМИД 22498897 . S2CID 16174225 .
- ^ Бассетт, Д.С.; Буллмор, Э.; Верчинский, бакалавр; Маттай, В.С.; Вайнбергер, доктор медицинских наук; Мейер-Линденберг, А. (10 сентября 2008 г.). «Иерархическая организация корковых сетей человека в здравоохранении и шизофрении» . Журнал неврологии . 28 (37): 9239–9248. doi : 10.1523/JNEUROSCI.1929-08.2008 . ISSN 0270-6474 . ПМЦ 2878961 . ПМИД 18784304 .
- ^ Восс, Мишель В.; Вонг, Челси Н.; Баникед, Полина Л.; Бёрдетт, Джонатан Х.; Эриксон, Кирк И.; Пракаш, Ручика Шаурья; Маколи, Эдвард; Лауриенти, Пол Дж.; Крамер, Артур Ф. (6 ноября 2013 г.). Сатиан, Криш (ред.). «Старение мозга с точки зрения сетевых наук: к чему стоит относиться позитивно?» . ПЛОС ОДИН . 8 (11): е78345. Бибкод : 2013PLoSO...878345V . дои : 10.1371/journal.pone.0078345 . ISSN 1932-6203 . ПМЦ 3819386 . ПМИД 24223147 .
- ^ Левит-Биннун, Нава; Давидович, Михаил; Голландия, Юлия (24 сентября 2013 г.). «Сенсорные и моторные вторичные симптомы как индикаторы уязвимости мозга» . Журнал расстройств нервного развития . 5 (1): 26. дои : 10.1186/1866-1955-5-26 . ISSN 1866-1947 . ПМК 3849186 . ПМИД 24063566 .
- ^ Коэн П. (26 мая 2004 г.). «Маленькие мировые сети – ключ к памяти» . Новый учёный .
- ^ Солла С (2004). «Самоподдерживающаяся активность в маленькой сети возбудимых нейронов» . Письма о физических отзывах . 92 (19). Калифорнийский университет в Санта-Барбаре, Институт теоретической физики Кавли: 198101. arXiv : nlin/0309067 . Бибкод : 2004PhRvL..92s8101R . doi : 10.1103/PhysRevLett.92.198101 . ПМИД 15169447 . S2CID 14272272 . Архивировано из оригинала 14 сентября 2016 г. Проверено 6 марта 2006 г.
- ^ Понтен СК, Бартоломей Ф, Стам СДЖ (апрель 2007 г.). «Сети малого мира и эпилепсия: графотеоретический анализ внутримозговых припадков в мезиальной височной доле». Клиническая нейрофизиология . 118 (4): 918–27. дои : 10.1016/j.clinph.2006.12.002 . ПМИД 17314065 . S2CID 35927833 .
Дальнейшее чтение
[ редактировать ]Книги
[ редактировать ]- Бьюкенен М (2003). Нексус: маленькие миры и новаторская теория сетей . Norton, WW & Company, Inc. ISBN 978-0-393-32442-6 .
- Дороговцев С.Н., Мендес Ж.Ф. (2003). Эволюция сетей: от биологических сетей к Интернету и WWW . Издательство Оксфордского университета. ISBN 978-0-19-851590-6 .
- Уоттс-ди-джей (1999). Маленькие миры: динамика сетей между порядком и случайностью . Издательство Принстонского университета. ISBN 978-0-691-00541-6 .
- Фаулер Дж. Х. (2005). «Явка в маленьком мире». В Цукермане А (ред.). Социальная логика политики . Издательство Университета Темпл. стр. 269–287.
Журнальные статьи
[ редактировать ]- Альберт Р., Барабаси А.Л. (2002). «Статистическая механика сложных сетей». Преподобный Мод. Физ . 74 (1): 47–97. arXiv : cond-mat/0106096 . Бибкод : 2002РвМП...74...47А . дои : 10.1103/RevModPhys.74.47 . S2CID 60545 .
- Барабаси А.Л., Альберт Р. (октябрь 1999 г.). «Появление масштабирования в случайных сетях». Наука . 286 (5439): 509–12. arXiv : cond-mat/9910332 . Бибкод : 1999Sci...286..509B . дои : 10.1126/science.286.5439.509 . ПМИД 10521342 . S2CID 524106 .
- Бартелеми М., Амарал Л.А. (1999). «Сети маленького мира: свидетельства перекрестной картины». Физ. Преподобный Летт . 82 (15): 3180–3183. arXiv : cond-mat/9903108 . Бибкод : 1999PhRvL..82.3180B . дои : 10.1103/PhysRevLett.82.3180 . S2CID 119398712 .
- Дороговцев С.Н., Мендес Ж.Ф. (2000). «Точно решаемая аналогия сетей маленького мира». Еврофиз. Летт . 50 (1): 1–7. arXiv : cond-mat/9907445 . Бибкод : 2000EL.....50....1D . дои : 10.1209/epl/i2000-00227-1 . S2CID 11334862 .
- Милгрэм С. (1967). «Проблема маленького мира». Психология сегодня . 1 (1): 60–67.
- Ньюман М. (2003). «Структура и функции сложных сетей». Обзор СИАМ . 45 (2): 167–256. arXiv : cond-mat/0303516 . Бибкод : 2003SIAMR..45..167N . дои : 10.1137/S003614450342480 . S2CID 65837 . pdf. Архивировано 14 марта 2021 г. в Wayback Machine.
- Равид Д., Рафаэли С. (2004). «Асинхронные дискуссионные группы как маленький мир и сети без масштабирования» . Первый понедельник . 9 (9). дои : 10.5210/fm.v9i9.1170 . S2CID 6388295 . [1]
Внешние ссылки
[ редактировать ]- Динамические сети близости , Сет Дж. Чендлер, Демонстрационный проект Wolfram .
- Запись о сетях малого мира в Scholarpedia (Мейсон А. Портер)