Категория модели

В математике , особенно в теории гомотопий , модельная категория — это категория с выделенными классами морфизмов («стрелок»), называемых « слабыми эквивалентностями », « расслоениями » и « корасслоениями », удовлетворяющими определенным связывающим их аксиомам. Они абстрагируются от категории топологических пространств или цепных комплексов ( теория производных категорий ). Эта концепция была представлена ​​Дэниелом Дж. Квилленом ( 1967 ).

В последние десятилетия язык модельных категорий использовался в некоторых разделах алгебраической К -теории и алгебраической геометрии , где гомотопически-теоретико-подходы привели к глубоким результатам.

Мотивация

Модельные категории могут обеспечить естественную основу для теории гомотопий : категория топологических пространств является модельной категорией, гомотопия которой соответствует обычной теории. Точно так же объекты, которые рассматриваются как пространства, часто допускают структуру модельных категорий, например категорию симплициальных множеств .

Другая модельная категория — это категория цепных комплексов R - коммутативного кольца R. модулей Гомотопическая теория в этом контексте является гомологической алгеброй . Гомологии затем можно рассматривать как тип гомотопии, позволяющий обобщать гомологии на другие объекты, такие как группы и R -алгебры , что является одним из первых основных применений теории. Из-за приведенного выше примера гомологии изучение замкнутых модельных категорий иногда называют гомотопической алгеброй .

Формальное определение

Первоначальное определение, данное Квилленом, было определением закрытой модельной категории, предположения которой в то время казались сильными, что побуждало других ослабить некоторые предположения для определения модельной категории. На практике это различие не оказалось существенным, и самые последние авторы (например, Марк Хови и Филип Хиршхорн) работают с категориями закрытой модели и просто опускают прилагательное «закрытый».

Определение было разделено на определение модельной структуры категории, а затем дальнейшие категориальные условия для этой категории, необходимость которых может сначала показаться немотивированной, но становится важной позже. Следующее определение следует за определением, данным Хови.

в Структура модели категории C состоит из трех выделенных классов морфизмов (эквивалентно подкатегорий): слабых эквивалентностей , расслоений и корасслоений , а также двух функториальных факторизаций. $(\alpha ,\beta )$ и $(\gamma ,\delta )$ при условии соблюдения следующих аксиом. Расслоение, которое также является слабой эквивалентностью, называется ациклическим (или тривиальным ) расслоением. а корасслоение, которое также является слабой эквивалентностью, называется ациклическим (или тривиальным ) корасслоением (или иногда называемым анодинным морфизмом ).

Аксиомы

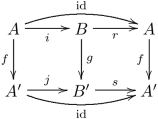
1. Ретракты : если — морфизм, принадлежащий одному из выделенных классов, а f — ретракт g g (как объекты в категории стрелок $C^{2}$, где 2 — упорядоченное множество из 2 элементов), то f принадлежит тому же выделенному классу. Явно требование, чтобы f было ретрактом g, означает, что существуют i , j , r и s , такие, что следующая диаграмма коммутирует:

   

2. 2 из 3 : если f и g — отображения в C такие, что gf определен, и любые два из них являются слабыми эквивалентностями, то и третье тоже.
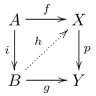
3. Лифтинг : ациклические корасслоения обладают свойством левого подъема по отношению к расслоениям, а корасслоения обладают свойством левого подъема по отношению к ациклическим расслоениям. Явно, если внешний квадрат следующей диаграммы коммутирует, где i — корасслоение, p — расслоение, а i или p — ациклическое, то существует h, завершающий диаграмму.

   

4. Факторизация :
   • каждый морфизм f в C можно записать как $p\circ i$ для расслоения p и ациклического корасслоения i ;
   • каждый морфизм f в C можно записать как $p\circ i$ для ациклического расслоения p и корасслоения i .

Модельная категория — это категория, имеющая модельную структуру и все (малые) пределы и копределы , т. е. полная и сополная категория с модельной структурой.

Определение через

Приведенное выше определение можно кратко сформулировать следующим эквивалентным определением: модельная категория — это категория C и три класса (так называемых) слабых эквивалентностей W , расслоений F и корасслоений C так, что

• C имеет все пределы и копределы,

• $(C\cap W,F)$ является слабой системой факторизации ,

• $(C,F\cap W)$ это слабая система факторизации
• $W$ удовлетворяет свойству 2 из 3.

Первые последствия определения

Из аксиом следует, что любые два из трех классов отображений определяют третий (например, корасслоения и слабые эквивалентности определяют расслоения).

Кроме того, определение самодвойственно: если C является модельной категорией, то ее противоположная категория ${\mathcal {C}}^{op}$ также допускает структуру модели, при которой слабые эквивалентности соответствуют своим противоположностям, расслоениям, противоположным корасслоениям, и корасслоениям, противоположным расслоениям.

Примеры

Топологические пространства

Категория топологических пространств Top . допускает стандартную модельную структуру категорий с обычными расслоениями (Серра) и слабыми эквивалентностями в качестве слабых гомотопических эквивалентностей Корасслоения — это не обычное понятие, встречающееся здесь , а скорее более узкий класс отображений, которые обладают свойством левого подъема по отношению к ациклическим расслоениям Серра.Эквивалентно, они являются ретрактами относительных клеточных комплексов, как объяснено, например, в «Категориях модели» Хови . Эта структура не уникальна; в общем, в данной категории может быть много структур категорий моделей. Для категории топологических пространств другая такая структура задается расслоениями Гуревича и стандартными корасслоениями, а слабыми эквивалентностями являются (сильные) гомотопические эквивалентности .

Цепные комплексы

Категория (неотрицательно градуированных) цепных комплексов -модулей R содержит по крайней мере две модельные структуры, обе из которых занимают видное место в гомологической алгебре:

• слабые эквивалентности — это отображения, индуцирующие изоморфизмы в гомологиях;
• корасслоения — это отображения, являющиеся мономорфизмами каждой степени с проективным коядром ; и
• расслоения - это отображения, которые являются эпиморфизмами в каждой ненулевой степени.

или

• слабые эквивалентности — это отображения, индуцирующие изоморфизмы в гомологиях;
• расслоения — это отображения, являющиеся эпиморфизмами каждой степени с инъективным ядром ; и
• корасслоения — это отображения, которые являются мономорфизмами в каждой ненулевой степени.

Это объясняет, почему Ext-группы R -модулей могут быть вычислены либо путем проективного разрешения источника, либо путем инъективного разрешения цели. Это кофибранты или замены фибрантов в соответствующих модельных структурах.

Категория произвольных цепных комплексов R -модулей имеет модельную структуру, определяемую формулой

• слабые эквивалентности — это цепные гомотопические эквивалентности цепных комплексов;
• корасслоения — это мономорфизмы, которые расщепляются как морфизмы лежащих в основе R -модулей; и
• расслоения — это эпиморфизмы, которые расщепляются как морфизмы лежащих в основе R -модулей.

Дальнейшие примеры

Другие примеры категорий, допускающих модельные структуры, включают категорию всех малых категорий, категорию симплициальных множеств или симплициальных предпучков на любом маленьком узле Гротендика , категорию топологических спектров и категории симплициальных спектров или предпучков симплициальных спектров на небольшом узле Гротендика. сайт.

Симплициальные объекты в категории являются частым источником модельных категорий; например, симплициальные коммутативные кольца или симплициальные R -модули допускают естественные модельные структуры. Это следует из того, что существует присоединение между симплициальными множествами и симплициальными коммутативными кольцами (задаваемыми забывающими и свободными функторами), и в хороших случаях можно поднять модельные структуры под присоединением.

Категория симплициальной модели — это симплициальная категория со структурой модели, совместимой с симплициальной структурой.

Учитывая любую категорию C и модельную категорию M , при некоторых дополнительных гипотезах категория функторов Fun ( C , M ) (также называемая C -диаграммами в M ) также является модельной категорией. Фактически, всегда есть два кандидата на различные структуры модели: в одной, так называемой проективной структуре модели, расслоения и слабые эквивалентности - это те карты функторов, которые являются расслоениями и слабыми эквивалентностями при вычислении на каждом объекте C . Двойственно, структура инъективной модели аналогична, но вместо этого используются корасслоения и слабые эквивалентности. В обоих случаях третий класс морфизмов задается условием поднятия (см. ниже). В некоторых случаях, когда категория C является категорией Риди , существует третья модельная структура, лежащая между проективной и инъективной.

Процесс превращения определенных карт в слабые эквивалентности в новой структуре категорий модели в той же базовой категории известен как локализация Боусфилда . Например, категорию симплициальных пучков можно получить как локализацию Боусфилда модельной категории симплициальных предпучков .

Дени-Шарль Цизински разработал общая теория модельных структур на предпучковых категориях (обобщающих симплициальных множествах, которые являются предпучками на симплексной категории ).

Если C является и категория Pro( C ) прообъектов в C. является модельной категорией, то такой же Однако структуру модели на Pro( C более слабый набор аксиом ) также можно построить, наложив на C .

Некоторые конструкции

Каждая закрытая модельная категория имеет терминальный объект по полноте и исходный объект по кополноте, поскольку эти объекты являются соответственно пределом и копределом пустой диаграммы. Для объекта X в категории модели, если уникальное отображение исходного объекта в X является корасслоением, то X называется кофибрантом . Аналогично, если уникальное отображение X в терминальный объект является расслоением, то X называется расслоением .

Если Z и X являются объектами модельной категории, такой что Z является кофибрантом и существует слабая эквивалентность от Z к X, то Z называется кофибрантной заменой для X . Аналогично, если Z является фибрантным и существует слабая эквивалентность X к Z, Z называется фибрантной заменой X то . В общем, не все объекты являются фибрантными или кофибрантными, хотя иногда это так. Например, все объекты являются кофибрантными в категории стандартной модели симплициальных множеств, и все объекты являются фибрантными для структуры категорий стандартной модели, приведенной выше для топологических пространств.

Левая гомотопия определяется относительно объектов-цилиндров , а правая гомотопия определяется относительно объектов пространства путей . Эти понятия совпадают, когда домен кофибрантен и кодомен фибрантен. В этом случае гомотопия определяет отношение эквивалентности на множествах hom в модельной категории, что приводит к появлению гомотопических классов.

расслоений и кофибраций по

Корасслоения можно охарактеризовать как отображения, обладающие свойством подъема влево по отношению к ациклическим расслоениям, а ациклические корасслоения характеризуются как отображения, обладающие свойством подъема влево по отношению к расслоениям. Точно так же расслоения можно охарактеризовать как отображения, обладающие свойством поднятия справа по отношению к ациклическим корасслоениям, а ациклические расслоения характеризуются как отображения, обладающие свойством поднятия справа по отношению к корасслоениям.

Гомотопия и гомотопическая категория

Гомотопическая категория модельной категории C это локализация C — относительно класса слабых эквивалентностей. Это определение гомотопической категории не зависит от выбора расслоений и корасслоений. Однако классы расслоений и корасслоений полезны для описания гомотопической категории по-другому и, в частности, для того, чтобы избежать теоретико-множественных проблем, возникающих при общей локализации категорий. Точнее, «фундаментальная теорема о модельных категориях» утверждает, что гомотопическая категория C эквивалентна категории, объектами которой являются объекты C , которые являются одновременно фибрантными и кофибрантными, и чьи морфизмы являются левыми гомотопическими классами отображений (что эквивалентно правым гомотопическим классам отображений). гомотопические классы отображений), определенные выше. (См., например, «Категории моделей» Хови, Thm 1.2.10)

Применяя это к категории топологических пространств с приведенной выше модельной структурой, получаемая гомотопическая категория эквивалентна категории CW-комплексов и гомотопических классов непрерывных отображений, откуда и происходит название.

Присоединения Квиллена

Пара сопряженных функторов

$F:C\leftrightarrows D:G$

между двумя модельными категориями C и D называется присоединением Квиллена, если F сохраняет корасслоения и ациклические корасслоения или, что то же самое, согласно аксиомам замкнутой модели, такое, что G сохраняет расслоения и ациклические расслоения. В этом случае F и G индуцируют присоединение

$LF:Ho(C)\leftrightarrows Ho(D):RG$

между гомотопическими категориями. Существует также явный критерий эквивалентности последнего ( в этом случае F и G называются эквивалентностью Квиллена ).

Типичным примером является стандартное соединение симплициальных множеств и топологических пространств:

$|-|:\mathbf {sSet} \leftrightarrows \mathbf {Top} :Sing$

включающий геометрическую реализацию симплициального множества и сингулярных цепей в некотором топологическом пространстве. Категории sSet и Top не эквивалентны, но являются их гомотопическими категориями. Поэтому симплициальные множества часто используются в качестве моделей топологических пространств из-за эквивалентности гомотопических категорий.

См. также

• (∞,1)-категория
• Категория коцикла
• Стабильная модельная категория

Ссылки

• Денис-Шарль Цисински: Предпучки как модели гомотопических типов , Asterisk, (308) 2006, xxiv+392 стр.
• Дуайер, Уильям Г .; Спалиньский, Ян (1995), «Гомотопические теории и модельные категории» (PDF) , Справочник по алгебраической топологии , Амстердам: Северная Голландия, стр. 73–126, doi : 10.1016/B978-044481779-2/50003-1 , ISBN  9780444817792 , МР   1361887
• Филип С. Хиршхорн: Категории моделей и их локализация , 2003, ISBN   0-8218-3279-4 .
• Марк Хови: Категории моделей , 1999, ISBN   0-8218-1359-5 .
• Клаус Хайнер Кампс и Тимоти Портер: Абстрактная гомотопия и простая теория гомотопии , 1997, World Scientific, ISBN   981-02-1602-5 .
• Жорж Мальциниотис: теория гомотопии Гротендика . Астериск, (301) 2005, vi+140 стр.

• Риль, Эмили (2014), Категорическая теория гомотопий , Cambridge University Press, doi : 10.1017/CBO9781107261457 , ISBN  978-1-107-04845-4 , МР   3221774

• Куиллен, Дэниел Г. (1967), Гомотопическая алгебра , Конспект лекций по математике, № 43, том. 43, Берлин, Нью-Йорк: Springer-Verlag , номер номера : 10.1007/BFb0097438 , ISBN.  978-3-540-03914-3 , МР   0223432

• Балчин, Скотт (2021), Справочник по категориям моделей , алгебре и приложениям, том. 27, Спрингер, номер домена : 10.1007/978-3-030-75035-0 , ISBN.  978-3-030-75034-3 , МР   4385504 , S2CID   240268465

Дальнейшее чтение

• «Нужны ли нам еще категории моделей?»
• "(бесконечность,1)-категории непосредственно из категорий модели"
• Пол Гёрсс и Кристен Шеммерхорн, Модельные категории и симплициальные методы

Внешние ссылки

• Категория модели в n Lab
• Категория моделей в каталабе Joyal