Giovanni Battista Riccioli

"Riccioli" redirects here. For other uses, see Riccioli (disambiguation).

Reverend Giovanni Battista Riccioli
Born	Galeazzo Riccioli (1598-04-17)17 April 1598 Ferrara, Papal States
Died	25 June 1671(1671-06-25) (aged 73) Bologna, Papal States
Nationality	Italian
Known for	Experiments with pendulums and with falling bodies Introducing the current scheme of lunar nomenclature
Parent(s)	Giovanni Battista Riccioli and Gaspara Riccioli (née Orsini)
Scientific career
Fields	Astronomy, experimental physics, geography, chronology

Giovanni Battista Riccioli, SJ (17 April 1598 – 25 June 1671) was an Italian astronomer and a Catholic priest in the Jesuit order. He is known, among other things, for his experiments with pendulums and with falling bodies, for his discussion of 126 arguments concerning the motion of the Earth, and for introducing the current scheme of lunar nomenclature. He is also widely known for discovering the first double star. He argued that the rotation of the Earth should reveal itself because on a rotating Earth, the ground moves at different speeds at different times.

Biography

Riccioli as portrayed in the 1742 Atlas Coelestis (plate 3) of Johann Gabriel Doppelmayer.

Riccioli was born in Ferrara. He entered the Society of Jesus on 6 October 1614. After completing his novitiate, he began to study humanities in 1616, pursuing those studies first at Ferrara, and then at Piacenza.

From 1620 to 1628 he studied philosophy and theology at the College of Parma. Parma Jesuits had developed a strong program of experimentation, such as with falling bodies. One of the most famous Italian Jesuits of the time, Giuseppe Biancani (1565–1624), was teaching at Parma when Riccioli arrived there. Biancani accepted new astronomical ideas, such as the existence of lunar mountains and the fluid nature of the heavens, and collaborated with the Jesuit astronomer Christoph Scheiner (1573–1650) on sunspot observations. Riccioli mentions him with gratitude and admiration.

By 1628 Riccioli's studies were complete and he was ordained. He requested missionary work, but that request was turned down. Instead, he was assigned to teach at Parma. There he taught logic, physics, and metaphysics from 1629 to 1632, and engaged in some experiments with falling bodies and pendulums. In 1632 he became a member of a group charged with the formation of younger Jesuits, among whom Daniello Bartoli. He spent the 1633–1634 academic year in Mantua, where he collaborated with Niccolò Cabeo (1576–1650) in further pendulum studies. In 1635 he was back at Parma, where he taught theology and also carried out his first important observation of the Moon. In 1636 he was sent to Bologna to serve as Professor of theology.

Riccioli described himself as a theologian, but one with a strong and ongoing interest in astronomy since his student days, when he studied under Biancani. He said that many Jesuits were theologians, but few were astronomers. He said that once the enthusiasm for astronomy arose within him he could never extinguish it, and so he became more committed to astronomy than theology. Eventually his superiors in the Jesuit order officially assigned him to the task of astronomical research. However, he also continued to write on theology (see below).

Riccioli built an astronomical observatory in Bologna at the College of St. Lucia, equipped with many instruments for astronomical observations, including telescopes, quadrants, sextants, and other traditional instruments. Riccioli dealt not only with astronomy in his research, but also with physics, arithmetic, geometry, optics, gnomonics, geography, and chronology. He collaborated with others in his work, including other Jesuits, most notably Francesco Maria Grimaldi (1618–1663) at Bologna, and he kept up a voluminous correspondence with others who shared his interests, including Hevelius, Huygens, Cassini, and Kircher.

He was awarded a prize by Louis XIV in recognition of his activities and their relevance to contemporary culture.

Riccioli continued to publish on both astronomy and theology up to his death. He died in Bologna at 73 years of age.

Scientific work

Almagestum Novum

The crescent phases of Venus and detailed representations of its appearance as seen through a telescope, from Riccioli's 1651 New Almagest.

One of Riccioli's most significant works was his 1651 Almagestum Novum (New Almagest), an encyclopedic work consisting of over 1500 folio pages (38 cm x 25 cm) densely packed with text, tables, and illustrations. It became a standard technical reference book for astronomers all over Europe: John Flamsteed (1646–1719), the first English astronomer royal, a Copernican and a Protestant, used it for his Gresham lectures; Jérôme Lalande (1732–1807) of the Paris Observatory cited it extensively even though it was an old book at that point; the 1912 Catholic Encyclopedia calls it the most important literary work of the Jesuits during the seventeenth century. Within its two volumes were ten "books" covering every subject within astronomy and related to astronomy at the time:

1. the celestial sphere and subjects such as celestial motions, the equator, ecliptic, zodiac, etc.
2. the Earth and its size, gravity and pendulum motion, etc.
3. the Sun, its size and distance, its motion, observations involving it, etc.
4. the Moon, its phases, its size and distance, etc. (detailed maps of the Moon as seen through a telescope were included)
5. lunar and solar eclipses
6. the fixed stars
7. the planets and their motions, etc. (representations of each as seen with a telescope were included);
8. comets and novae ("new stars")
9. the structure of the universe—the heliocentric and geocentric theories, etc.
10. calculations related to astronomy.

Riccioli envisioned that the New Almagest would have three volumes, but only the first (with its 1500 pages split into two parts) was completed.

Pendulums and falling bodies

Riccioli is credited with being the first person to precisely measure the acceleration due to gravity of falling bodies. Books 2 and 9 of the New Almagest Riccioli included a significant discussion of and extensive experimental reports on the motions of falling bodies and pendulums.

He was interested in the pendulum as a device for precisely measuring time. By counting the number of pendulum swings that elapsed between transits of certain stars, Riccioli was able to experimentally verify that the period of a pendulum swinging with small amplitude is constant to within two swings out of 3212 (0.062%). He also reported that a pendulum's period increases if the amplitude of its swing is increased to 40 degrees. He sought to develop a pendulum whose period was precisely one second – such a pendulum would complete 86,400 swings in a 24-hour period. This he directly tested, twice, by using stars to mark time and recruiting a team of nine fellow Jesuits to count swings and maintain the amplitude of swing for 24 hours. The results were pendulums with periods within 1.85%, and then 0.69%, of the desired value; and Riccioli even sought to improve on the latter value. The seconds pendulum was then used as a standard for calibrating pendulums with different periods. Riccioli said that for measuring time a pendulum was not a perfectly reliable tool, but in comparison with other methods it was an exceedingly reliable tool.

With pendulums to keep time (sometimes augmented by a chorus of Jesuits chanting in time with a pendulum to provide an audible timer) and a tall structure in the form of Bologna's Torre de Asinelli from which to drop objects, Riccioli was able to engage in precise experiments with falling bodies. He verified that falling bodies followed Galileo's "odd-number" rule so that the distance travelled by a falling body increases in proportion to the square of the time of fall, indicative of constant acceleration. According to Riccioli, a falling body released from rest travels 15 Roman feet (4.44 m) in one second, 60 feet (17.76 m) in two seconds, 135 feet (39.96 m) in three seconds, etc. Other Jesuits such as the above-mentioned Cabeo had argued that this rule had not been rigorously demonstrated. His results showed that, while falling bodies generally showed constant acceleration, there were differences determined by weight and size and density. Riccioli said that if two heavy objects of differing weight are dropped simultaneously from the same height, the heavier one descends more quickly so long as it is of equal or greater density; if both objects are of equal weight the denser one descends more quickly.

For example, in dropping balls of wood and lead that both weighed 2.5 ounces, Riccioli found that upon the leaden ball having traversed 280 Roman feet the wooden ball had traversed only 240 feet (a table in the New Almagest contains data on twenty one such paired drops). He attributed such differences to the air, and noted that air density had to be considered when dealing with falling bodies. He illustrated the reliability of his experiments by providing detailed descriptions of how they were carried out, so that anyone could reproduce them, complete with diagrams of the Torre de Asinelli that showed heights, drop locations, etc.

Riccioli noted that while these differences did contradict Galileo's claim that balls of differing weight would fall at the same rate, it was possible Galileo observed the fall of bodies made of the same material but of differing sizes, for in that case the difference in fall time between the two balls is much smaller than if the balls are of same size but differing materials, or of the same weight but differing sizes, etc., and that difference is not apparent unless the balls are released from a very great height. At the time, various people had expressed concern with Galileo's ideas about falling bodies, arguing that it would be impossible to discern the small differences in time and distance needed to adequately test Galileo's ideas, or reporting that experiments had not agreed with Galileo's predictions, or complaining that suitably tall buildings with clear paths of fall were not available to thoroughly test Galileo's ideas. By contrast, Riccioli was able to show that he had carried out repeated, consistent, precise experiments in an ideal location. Thus as D. B. Meli notes,

Riccioli's accurate experiments were widely known during the second half of the [seventeenth] century and helped forge a consensus on the empirical adequacy of some aspects of Galileo's work, especially the odd-number rule and the notion that heavy bodies fall with similar accelerations and speed is not proportional to weight. His limited agreement with Galileo was significant, coming as it did from an unsympathetic reader who had gone so far as to include the text of Galileo's condemnation in his own publications.

Work concerning the Moon

Map of the Moon from the New Almagest.

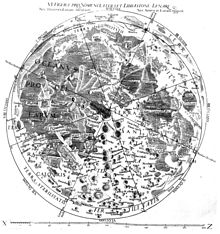
Riccioli and Grimaldi extensively studied the Moon, of which Grimaldi drew maps. This material was included in Book 4 of the New Almagest. Grimaldi's maps were based on earlier work by Johannes Hevelius and Michael van Langren. On one of these maps, Riccioli provided names for lunar features—names that are the basis for the nomenclature of lunar features still in use today. For example, Mare Tranquillitatis (The Sea of Tranquility, site of the Apollo 11 landing in 1969), received its name from Riccioli. Riccioli named large lunar areas for weather. He named craters for significant astronomers, grouping them by philosophies and time periods. Although Riccioli rejected the Copernican theory, he named a prominent lunar crater "Copernicus", and he named other important craters after other proponents of the Copernican theory such as Kepler, Galileo and Lansbergius. Because craters that he and Grimaldi named after themselves are in the same general vicinity as these, while craters named for some other Jesuit astronomers are in a different part of the Moon, near the very prominent crater named for Tycho Brahe, Riccioli's lunar nomenclature has at times been considered to be a tacit expression of sympathy for a Copernican theory that, as a Jesuit, he could not publicly support. However, Riccioli said he put the Copernicans all in stormy waters (the Oceanus Procellarum). Another noteworthy feature of the map is that Riccioli included on it a direct statement that the Moon is not inhabited. This ran counter to speculations about an inhabited Moon that had been present in the works of Nicholas of Cusa, Giordano Bruno, and even Kepler, and which would continue on in works of later writers such as Bernard de Fontenelle and William Herschel.

Arguments concerning the motion of the Earth

Frontispiece of Riccioli's 1651 New Almagest. Mythological figures observe the heavens with a telescope and weigh the heliocentric theory of Copernicus in a balance against his modified version of Tycho Brahe's geo-heliocentric system, in which the Sun, Moon, Jupiter, and Saturn orbit the Earth while Mercury, Venus, and Mars orbit the Sun. The old Ptolemaic geocentric theory lies discarded on the ground, made obsolete by the telescope's discoveries. These are illustrated at top and include phases of Venus and Mercury and a surface feature on Mars (left), moons of Jupiter, rings of Saturn, and features on the Moon (right). The balance tips in favor of Riccioli's "Tychonic" system.

A substantial portion of the New Almagest (Book 9, consisting of 343 pages) is devoted to an analysis of the world system question: Is the universe geocentric or heliocentric? Does the Earth move or is it immobile? The historian of science Edward Grant has described Book 9 as being the "probably the lengthiest, most penetrating, and authoritative" analysis of this question made by "any author of the sixteenth and seventeenth centuries", in his opinion apparently superseding even Galileo's Dialogue Concerning the Two Chief World Systems — Ptolemaic and Copernican. Indeed, one writer has recently described Book 9 as "the book Galileo was supposed to write". Within Book 9 Riccioli discusses 126 arguments concerning Earth's motion — 49 for and 77 against. To Riccioli the question was not between the geocentric world system of Ptolemy and the heliocentric world system of Copernicus, for the telescope had unseated the Ptolemaic system; it was between the geo-heliocentric world system developed by Tycho Brahe in the 1570s (in which the Sun, Moon, and stars circle an immobile Earth, while the planets circle the Sun – sometimes called a "geo-heliocentric" or "hybrid" system) and that of Copernicus. As the frontispiece of the New Almagest illustrates (see figure at right), Riccioli favoured a modified version of Tycho Brahe's system; here is how he described the system that "came to [his] mind" when he was in Parma : "it shares everything with the Tychonian system, except the orbits of Saturn and Jupiter; for [me] their center was not the Sun, but Earth itself".

Many writers make references to Riccioli's analysis and the 126 arguments. However, translations of arguments of the New Almagest, and discussions of the arguments to any extent by more modern writers are rare: only for three arguments of the 126 are such translations and discussions readily available. These are, first, an argument Riccioli called the "physico-mathematical argument", which was related to one of Galileo's conjectures; second, an argument based on what today is known as the "Coriolis effect"; third, an argument based on the appearance of stars as seen through the telescopes of the time.

The "physico-mathematical" argument

Riccioli discusses the physico-mathematical argument in regard to arguments both for and against Earth's motion. Galileo offered a conjecture in his 1632 Dialogue that the apparent linear acceleration of a stone falling from a tower was the result of two uniform circular motions acting in combination – the daily rotation of Earth, and a second uniform circular motion belonging to the stone and acquired from being carried along by the tower. Galileo says that

[T]he true and real motion of the stone is never accelerated at all, but is always equable and uniform.... So we need not look for any other causes of acceleration or any other motions, for the moving body, whether remaining on the tower or falling, moves always in the same manner; that is, circularly, with the same rapidity, and with the same uniformity.... if the line described by a falling body is not exactly this, it is very near to it... [and] according to these considerations, straight motion goes entirely out the window and nature never makes any use of it at all.

Riccioli explained that this conjecture could not work: It could not apply to the fall of bodies near the Earth's poles, where there would be little or no circular motion caused by Earth's rotation; and even at the equator where there would be more motion caused by Earth's rotation, the rate of fall predicted by Galileo's idea was too slow. Riccioli argued that the problems with Galileo's conjecture were a mark against the Copernican world system, but modern writers differ in regards to Riccioli's reasoning on this.

The "coriolis effect" argument

Illustration from Riccioli's 1651 New Almagest showing the effect a rotating Earth should have on projectiles. When the cannon is fired at eastern target B, cannon and target both travel east at the same speed while the ball is in flight. The ball strikes the target just as it would if the Earth were immobile. When the cannon is fired at northern target E, the target moves more slowly to the east than the cannon and the airborne ball, because the ground moves more slowly at more northern latitudes (the ground hardly moves at all near the pole). Thus the ball follows a curved path over the ground, not a diagonal, and strikes to the east, or right, of the target at G.

Riccioli also argued that the rotation of the Earth should reveal itself in the flight of artillery projectiles, because on a rotating Earth the ground moves at different speeds at different latitudes. He wrote that

If a ball is fired along a Meridian toward the pole (rather than toward the East or West), diurnal motion will cause the ball to be carried off [that is, the trajectory of the ball will be deflected], all things being equal: for on parallels of latitude nearer the poles, the ground moves more slowly, whereas on parallels nearer the equator, the ground moves more rapidly.

Therefore, were a cannon, aimed directly at a target to the north, to fire a ball, that ball would strike slightly to the east (right) of the target, thanks to the Earth's rotation. But, if the cannon were fired to the east there would be no deflection, as both cannon and target would move the same distance in the same direction. Riccioli said that the best of cannoneers could fire a ball right into the mouth of an enemy's cannon; if this deflection effect existed in northward shots they would have detected it. Riccioli argued that the absence of this effect indicated that the Earth does not rotate. He was correct in his reasoning in that the effect he describes actually does occur. It is known today as the Coriolis effect after the nineteenth-century physicist Gaspard-Gustave Coriolis (1792–1843). However, the rightward deflection actually occurs regardless of the direction the cannon is pointed (a much more developed understanding of physics than what was available in Riccioli's time is required to explain this). At any rate, the effect would have been too small for cannoneers of the time to detect.

The star size argument

Riccioli also used telescopic observations of stars to argue against the Copernican theory. Viewed through the small telescopes of his time, stars appeared as small but distinct disks. These disks were spurious – caused by the diffraction of waves of light entering the telescope. Today they are known as Airy disks, after the nineteenth-century astronomer George Biddell Airy (1801–1892). The real disks of stars are generally too tiny to be seen even with the best of modern telescopes. But during most of the seventeenth century it was thought that these disks seen in a telescope were the actual bodies of stars. In the Copernican theory, the stars had to lie at vast distances from Earth in order to explain why no annual parallax was seen among them. Riccioli and Grimaldi made numerous measurements of star disks using a telescope, providing a detailed description of their procedure so that anyone who wanted could replicate it. Riccioli then calculated the physical sizes that the measured stars would need to have in order for them both to be as far away as was required in the Copernican theory to show no parallax, and to have the sizes seen with the telescope. The result in all cases was that the stars were huge – dwarfing the sun. In some scenarios one single star would exceed the size of the entire universe as estimated by a geocentrist like Tycho Brahe. This problem that the appearance of stars in the telescope posed for the Copernican theory had been noted as early as 1614 by Simon Marius, who said telescopic observations of the disks of stars supported the Tychonic theory. The problem was acknowledged by Copernicans such as Martin van den Hove (1605–1639), who also measured the disks of stars and acknowledged that the issue of vast star sizes might lead people to reject the Copernican theory.

Other arguments

The other arguments Riccioli presents in Book 9 of the New Almagest were diverse. There were arguments concerning: whether buildings could stand or birds could fly if Earth rotated; what sorts of motions were natural to heavy objects; what constitutes the more simple and elegant celestial arrangement; whether the heavens or the Earth was the more suited for motion and the more easily and economically moved; whether the center of the universe was a more or less noble position; and many others. Many of the anti-Copernican arguments in the New Almagest had roots in the anti-Copernican arguments of Tycho Brahe.

Riccioli argued vigorously against the Copernican system, and even characterized certain arguments for terrestrial immobility as unanswerable. However, he also rebutted certain anti-Copernican arguments, siding with the Copernicans in his assertions that rotation of the Earth would not necessarily be felt, and that it would not ruin buildings or leave birds behind. Some authors have suggested that Riccioli may have been a secret Copernican, required due to his position as a Jesuit to pretend to oppose the theory.

The Astronomia Reformata (Reformed Astronomy)

Another prominent astronomical publication of Riccioli's was his 1665 Astronomia Reformata (Reformed Astronomy)—another large volume, although only half the length of the New Almagest. The contents of the two significantly overlap; the Reformed Astronomy might be thought of as a condensed and updated version of the New Almagest.

Representations from Riccioli's 1665 Reformed Astronomy of Saturn's changing appearance.

The Reformed Astronomy contains an extensive report on the changing appearance of Saturn. Included in the section on Jupiter is an apparent record of a very early (if not the earliest) observation of Jupiter's Great Red Spot, made by Leander Bandtius, Abbot of Dunisburgh and owner of a particularly fine telescope, in late 1632. Also in that section Riccioli includes reports of Jovian cloud belts appearing and disappearing over time.

The appearance of the physico-mathematical argument in the Reformed Astronomy was the occasion for Stefano degli Angeli (1623–1697) to launch an "unexpected, somewhat disrespectful and sometimes flippant attack" on Riccioli and the argument. James Gregory published a report in England in 1668 on the resulting public and personal dispute on the matter of falling objects. This was a prelude to Robert Hooke's (1635–1703) invitation to Isaac Newton (1642–1727) to resume his scientific correspondence with the Royal Society, and to their ensuing discussion about the trajectory of falling bodies "that turned Newton's mind away from 'other business' and back to the study of terrestrial and celestial mechanics." The Reformed Astronomy featured an adaptation to the accumulating observational evidence in favor of Johannes Kepler's elliptical celestial mechanics: it incorporated elliptical orbits into the geo-heliocentric Tychonic theory. Riccioli accepted Kepler's ideas, but remained opposed to the heliocentric theory. Indeed, following the dispute with Angeli, Riccioli's attitude toward heliocentrism hardened.

Other work

Between 1644 and 1656, Riccioli was occupied by topographical measurements, working with Grimaldi, determining values for the circumference of Earth and the ratio of water to land. Defects of method, however, gave a less accurate value for degrees of arc of the meridian than Snellius had achieved a few years earlier. Snellius had been mistaken by approximately 4,000 meters; but Riccioli was more than 10,000 meters in error. Riccioli had come up with 373,000 pedes despite the fact that references to a Roman degree in antiquity had always been 75 milliaria or 375,000 pedes.

He is often credited with being one of the first to telescopically observe the star Mizar and note that it was a double star; however, Castelli and Galileo observed it much earlier.

In the words of Alfredo Dinis,

Riccioli enjoyed great prestige and great opposition, both in Italy and abroad, not only as a man of encyclopedic knowledge but also as someone who could understand and discuss all the relevant issues in cosmology, observational astronomy, and geography of the time.

Selected works

Riccioli's works are in Latin.

Astronomy

Geographicae crucis fabrica et usus ad repraesentandam mira facilitate omnem dierum noctiumque ortuum solis et occasum, horarumque omnium varietatem, 1643

• Geographicae crucis fabrica et usus ad repraesentandam ... omnem dierum noctiumque ortuum solis et occasum (Ferroni: 1643) (Map of the world from Gallica)
• Geographicae crucis fabrica et usus ad repraesentandam mira facilitate omnem dierum noctiumque ortuum solis et occasum, horarumque omnium varietatem (in Latin). Bologna: Giovanni Battista Ferroni. 1643.
• Almagestum novum astronomiam veterem novamque complectens observationibus aliorum et propriis novisque theorematibus, problematibus ac tabulis promotam (Vol. I–III, 1651) (Or: Volume 1 : First part at Google Books; Second part at Google Books)
• Geographiæ et hydrographiæ reformatæ libri duodecim at Google Books, Bologna, 1661
  • Geographiæ et hydrographiæ reformatæ: nuper recognitæ & auctæ libri duodecim at Google Books. 2nd ed., Venice, 1672. 695 p.
• Astronomia reformata (Vol. I–II, 1665)
  • Volume 1 at Google Books: Observations, hypotheses and explanations
  • Volume 2 at Google Books: Directions for use, and the 102 tables
• Vindiciae calendarii Gregoriani adversus Franciscum Leveram (1666)
• Argomento fisicomattematico contro il moto diurno della terra (in Italian). Bologna: Emilio Maria Manolessi & fratelli. 1668.
• Apologia R.P. Io. Bapt. Riccioli Societatis Iesu pro argumento physicomathematico contra systema Copernicanum (1669)
• Chronologiae reformatae et ad certas conclusiones redactae ... (Vol. I–IV, 1669)
  • ... tomus primus continens doctrinam temporum at Google Books, 404 p.
  • ... tomus secundus Aetates Mundi Et Tria Chronica Continens at Google Books, 236 p.
  • ... tomus tertius continens catalogos plurimos personarum rerumque insigniorum cum earum temporibus, at Google Books 161p. & tomus quartus 324 p,
• Tabula latitudinum et longitudinum (1689)
• Tabula latitudinum et longitudinum (in Spanish). Cordoba: Antonio Serrano. 1744.

Theology

• Evangelium unicum Domini nostri Jesu Christi ex verbis ipsis quatuor Evangelistarum conflatum et in meditationes distributum at Google Books. Bologna, 1667, 466 p.
• Immunitas ab errore tam speculativo quam practico definitionum s. Sedis apostolicae in canonizatione sanctorum, in festorum ecclesiasticorum institutione et in decisione dogmatum, quae in verbo Dei scripto, traditove implicite tantum continentur, aut ex alterutro sufficienter deducuntur, Bologna, 1668 (Listed in the Index Librorum Prohibitorum in 1669)
• De distinctionibus entium in Deo et in creaturis tractatus philosophicus ac theologicus (1669)

Selected editions of Riccioli's books about prosody

Riccioli's books about prosody were revised many times and underwent many editions.

• Prosodia Bonnoniensis reformata .... Bologne, 1655
• Prosodia Bononiensis reformata at Google Books. Padua, 1714 (the two volumes merged into one)

See also

• List of Jesuit scientists
• List of Roman Catholic scientist-clerics
• Grimaldi (crater)
• Riccioli (crater)

Notes

• Peter, Barker. "Voxcanis". Retrieved 29 November 2018.

References

• AlunSalt: "Copernicus and the Star that was bigger than the Universe" (17 January 2011)
• Graney, Christopher M. (2011). "126 Arguments Concerning the Motion of the Earth, as presented by Giovanni Battista Riccioli in his 1651 Almagestum Novum". arXiv:1103.2057 [physics.hist-ph].
• BBC News 2010: "Jupiter's brown stripe is returning, say astronomers" (26 November 2010)
• Bolt, Marvin (ed.) 2007, Mapping the Universe (Chicago: Adler Planetarium & Astronomy Museum)
•  Brock, Henry Matthias (1912). "Giovanni Battista Riccioli". In Herbermann, Charles (ed.). Catholic Encyclopedia. Vol. 13. New York: Robert Appleton Company.
• Campbell, Thomas Joseph 1921, The Jesuits, 1534–1921: a history of the Society of Jesus from its foundation to the present time (New York: Encyclopedia Press)
• Comins, N. F. & Kaufmann, W. J. 2009, Discovering the Universe: From the Stars to the Planets (New York: W. H. Freeman)
• Crowe, M. J. 2008 The Extraterrestrial Life Debate, Antiquity to 1915: A Source Book (University of Notre Dame Press)
• Delambre J. B. J. 1821, Histoire de L'astronomie moderne (Paris)
• Dialogue Concerning the Two Chief World Systems 2001, by Galileo Galilei [1632], translated and with revised notes by Stillman Drake and foreword by Albert Einstein (New York: Random House/The Modern Library)
• Discover News 2011: "Did Riccioli 'Discover' the Coriolis Effect?" Archived 7 October 2012 at the Wayback Machine, Jennifer Ouellette (27 January 2011)
• Dinis, Alfredo 2002, "Was Riccioli a Secret Copernican?" in Giambattista Riccioli e il Merito Scientifico dei Gesuiti nell'età Barocca, a cura di Maria Teresa Borgato (Firenze: Leo S. Olschki), 49–77
• Dinis, Alfredo 2003, "Giovanni Battista Riccioli and the Science of His Time" in Jesuit Science and the Republic of Letters, p. 195, at Google Books, edited by Mordechai Feingold (Cambridge, Massachusetts: MIT Press), 195–224 (Significant excerpts)
• Galloway, T. 1842, Remarks on Fernel's Measure of a Degree, p. 90, at Google Books, Philosophical Magazine and Journal of Science, Volume 20, 90–98
• Gingerich, Owen 1973, "Copernicus and Tycho", Scientific American, Volume 229, 86–101.
• Graney, Christopher M. (2010). "The Telescope Against Copernicus: Star Observations by Riccioli Supporting a Geocentric Universe". Journal for the History of Astronomy. 41 (4): 453. Bibcode:2010JHA....41..453G. doi:10.1177/002182861004100402. S2CID 117782745.
• Graney, Christopher M. (2010). "Changes in the Cloud Belts of Jupiter, 1630-1664, as Reported in the 1665 Astronomia Reformata of Giovanni Battista Riccioli". Baltic Astronomy. 19 (3–4): 265. arXiv:1008.0566. Bibcode:2010BaltA..19..265G. doi:10.1515/astro-2017-0425.
• Graney, Christopher M. (2011). "Coriolis effect, two centuries before Coriolis". Physics Today. 64 (8): 8–9. Bibcode:2011PhT....64h...8G. doi:10.1063/PT.3.1195. S2CID 121193379.
• Graney, Christopher M.; Grayson, Timothy P. (2011). "On the Telescopic Disks of Stars: A Review and Analysis of Stellar Observations from the Early Seventeenth through the Middle Nineteenth Centuries". Annals of Science. 68 (3): 351–373. arXiv:1003.4918. doi:10.1080/00033790.2010.507472. S2CID 118007707.
• Graney, Christopher M. (2012). "Anatomy of a fall: Giovanni Battista Riccioli and the story of g". Physics Today. 65 (9): 36–40. Bibcode:2012PhT....65i..36G. doi:10.1063/PT.3.1716.
• Graney, C. M. 2015, Setting Aside All Authority: Giovanni Battista Riccioli and the Science against Copernicus in the Age of Galileo, University of Notre Dame Press, ISBN 978-0268029883
• Grant, Edward 1984, "In Defense of the Earth's Centrality and Immobility: Scholastic Reaction to Copernicanism in the Seventeenth Century", Transactions of the American Philosophical Society, New Series, Volume 74, 1–69
• Grant, Edward 1996, Planets, Stars, and Orbs: The Medieval Cosmos, 1200–1687 (Cambridge: Cambridge University Press)
• Heilbron, J. L. 1999, The Sun in the Church: Cathedrals as Solar Observatories (Cambridge, Massachusetts: Harvard University Press)
• Hoefer, Ferdinand 1873, Histoire de l'astronomie (Paris)
• Koyré, Alexandre (1955). "A Documentary History of the Problem of Fall from Kepler to Newton: De Motu Gravium Naturaliter Cadentium in Hypothesi Terrae Motae". Transactions of the American Philosophical Society. 45 (4): 329–395. doi:10.2307/1005755. JSTOR 1005755.
• Meli, Domenico Bertoloni 2006, Thinking with Objects: The Transformation of Mechanics in the Seventeenth Century (Baltimore, Maryland: Johns Hopkins University Press)
• New Scientist 2010: "Jupiter loses a stripe", David Shiga (11 May 2010)
• New Scientist 2011: "Coriolis-like effect found 184 years before Coriolis", MacGregor Campbell (14 January 2011); "Forces and Fate", New Scientist (print edition 8 January 2011), 6
• Raphael, Renee 2011, "A non-astronomical image in an astronomical text: Visualizing motion in Riccioli's Almagestum Novum", Journal for the History of Astronomy, Volume 42, 73–90
• The TOF Spot: "The Book Galileo Was Supposed to Write" (21 April 2011)
• Van Helden, Albert 1984, "Galileo, Telescopic Astronomy, and the Copernican System", in The General History of Astronomy, edited by M. A. Hoskin, volume 2A, (Cambridge: Cambridge University Press)
• Whitaker, E. A. 1999, Mapping and Naming the Moon: A History of Lunar Cartography and Nomenclature (Cambridge University Press)
• F. Marcacci, Cieli in contraddizione: Giovanni Battista Riccioli e il terzo sistema del mondo, Modena-Perugia, Accademia delle Scienze-Aguaplano 2018.
• Marcacci, Flavia (2023). "G.B. Riccioli's geo-heliocentric use of Epicepicycles , ellipses and spirals". Journal for the History of Astronomy. 54 (2): 171–192. Bibcode:2023JHA....54..171M. doi:10.1177/00218286231165331. S2CID 258548319.
• Marcacci, Flavia (2018). "La scienza e l'ipotesi assoluta. Metodologia e logica della ricerca nell' Almagestum novum di Giovanni Battista Riccioli". Archives Internationales d'Histoire des Sciences. 68 (180–181): 72–107. doi:10.1484/J.ARIHS.5.120152.
• Marcacci, Flavia (2021). "Seeing at a Glance". Nuncius. 36: 119–142. doi:10.1163/18253911-bja10010. S2CID 233568069.

External links

• Media related to Giovanni Riccioli at Wikimedia Commons
• Brief Riccioli biography from the Catholic Encyclopedia.
• Facts about Riccioli from Rice University's Galileo Project.
• Riccioli, Giovanni Battista (French)
• Almagestum novum astronomiam in PDF form