Eyeball theorem

eyeball theorem, red chords are of equal length
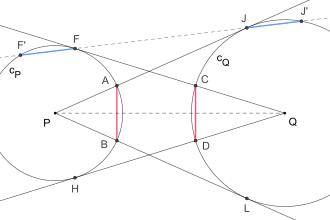
theorem variation, blue chords are of equal length

The eyeball theorem is a statement in elementary geometry about a property of a pair of disjoined circles.

More precisely it states the following:

For two nonintersecting circles $c_{P}$ and $c_{Q}$centered at $P$ and $Q$ the tangents from P onto $c_{Q}$ intersect $c_{Q}$ at $C$ and $D$ and the tangents from Q onto $c_{P}$ intersect $c_{P}$ at $A$ and $B$. Then $|AB|=|CD|$.

The eyeball theorem was discovered in 1960 by the Peruvian mathematician Antonio Gutierrez. However without the use of its current name it was already posed and solved as a problem in an article by G. W. Evans in 1938. Furthermore Evans stated that problem was given in an earlier examination paper.

A variant of this theorem states, that if one draws line $FJ$ in such a way that it intersects $c_{P}$ for the second time at $F'$ and $c_{Q}$ at $J'$. Then, it turns out that $|FF'|=|JJ'|$.

There are some proofs for Eyeball theorem, one of them show that this theorem is a consequence of the Japanese theorem for cyclic quadrilaterals.

See also

• Japanese theorem for cyclic quadrilaterals

Further reading

• Antonio Gutierrez: Eyeball theorems. In: Chris Pritchard (ed.): The Changing Shape of Geometry. Celebrating a Century of Geometry and Geometry Teaching. Cambridge University Press, 2003, ISBN 9780521531627, pp. 274–280

External links

• Weisstein, Eric W. "Eyeball Theorem". MathWorld.
• Eyeball Theorem at Geometry from the Land of the Incas