Spherical polyhedron


In geometry, a spherical polyhedron or spherical tiling is a tiling of the sphere in which the surface is divided or partitioned by great arcs into bounded regions called spherical polygons. Much of the theory of symmetrical polyhedra is most conveniently derived in this way.
The most familiar spherical polyhedron is the soccer ball, thought of as a spherical truncated icosahedron. The next most popular spherical polyhedron is the beach ball, thought of as a hosohedron.
Some "improper" polyhedra, such as hosohedra and their duals, dihedra, exist as spherical polyhedra, but their flat-faced analogs are degenerate. The example hexagonal beach ball, {2, 6}, is a hosohedron, and {6, 2} is its dual dihedron.
History
[edit]During the 10th Century, the Islamic scholar Abū al-Wafā' Būzjānī (Abu'l Wafa) studied spherical polyhedra as part of a work on the geometry needed by craftspeople and architects.[1]
The work of Buckminster Fuller on geodesic domes in the mid 20th century triggered a boom in the study of spherical polyhedra.[2] At roughly the same time, Coxeter used them to enumerate all but one of the uniform polyhedra, through the construction of kaleidoscopes (Wythoff construction).[3]
Examples
[edit]All regular polyhedra, semiregular polyhedra, and their duals can be projected onto the sphere as tilings:
| Schläfli symbol |
{p,q} | t{p,q} | r{p,q} | t{q,p} | {q,p} | rr{p,q} | tr{p,q} | sr{p,q} |
|---|---|---|---|---|---|---|---|---|
| Vertex config. |
pq | q.2p.2p | p.q.p.q | p.2q.2q | qp | q.4.p.4 | 4.2q.2p | 3.3.q.3.p |
| Tetrahedral symmetry (3 3 2) |
 33 |
 3.6.6 |
 3.3.3.3 |
 3.6.6 |
 33 |
 3.4.3.4 |
 4.6.6 |
 3.3.3.3.3 |
 V3.6.6 |
 V3.3.3.3 |
 V3.6.6 |
 V3.4.3.4 |
 V4.6.6 |
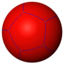 V3.3.3.3.3 | |||
| Octahedral symmetry (4 3 2) |
 43 |
 3.8.8 |
 3.4.3.4 |
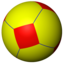 4.6.6 |
 34 |
 3.4.4.4 |
 4.6.8 |
 3.3.3.3.4 |
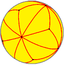 V3.8.8 |
 V3.4.3.4 |
 V4.6.6 |
 V3.4.4.4 |
 V4.6.8 |
 V3.3.3.3.4 | |||
| Icosahedral symmetry (5 3 2) |
 53 |
 3.10.10 |
 3.5.3.5 |
 5.6.6 |
 35 |
 3.4.5.4 |
 4.6.10 |
 3.3.3.3.5 |
 V3.10.10 |
 V3.5.3.5 |
 V5.6.6 |
 V3.4.5.4 |
 V4.6.10 |
 V3.3.3.3.5 | |||
| Dihedral example (p=6) (2 2 6) |
 62 |
 2.12.12 |
 2.6.2.6 |
 6.4.4 |
 26 |
 2.4.6.4 |
 4.4.12 |
 3.3.3.6 |

| n | 2 | 3 | 4 | 5 | 6 | 7 | ... |
|---|---|---|---|---|---|---|---|
| n-Prism (2 2 p) |

|

|

|

|

|

|
... |
| n-Bipyramid (2 2 p) |

|

|

|

|

|

|
... |
| n-Antiprism | 
|

|

|
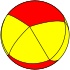
|

|

|
... |
| n-Trapezohedron | 
|

|

|

|

|

|
... |
Improper cases
[edit]Spherical tilings allow cases that polyhedra do not, namely hosohedra: figures as {2,n}, and dihedra: figures as {n,2}. Generally, regular hosohedra and regular dihedra are used.
| Space | Spherical | Euclidean | |||||
|---|---|---|---|---|---|---|---|
| Tiling name |
Henagonal hosohedron |
Digonal hosohedron |
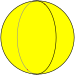
Trigonal hosohedron |
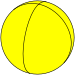
Square hosohedron |
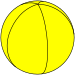
Pentagonal hosohedron |
... | Apeirogonal hosohedron |
| Tiling image |

|
|

|
|
|
... | |
| Schläfli symbol |
{2,1} | {2,2} | {2,3} | {2,4} | {2,5} | ... | {2,∞} |
| Coxeter diagram |
... | ||||||
| Faces and edges |
1 | 2 | 3 | 4 | 5 | ... | ∞ |
| Vertices | 2 | 2 | 2 | 2 | 2 | ... | 2 |
| Vertex config. |
2 | 2.2 | 23 | 24 | 25 | ... | 2∞ |
| Space | Spherical | Euclidean | |||||
|---|---|---|---|---|---|---|---|
| Tiling name |
Monogonal dihedron |
Digonal dihedron |
Trigonal dihedron |
Square dihedron |
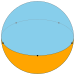
Pentagonal dihedron |
... | Apeirogonal dihedron |
| Tiling image |

|

|

|

|
|
... | |
| Schläfli symbol |
{1,2} | {2,2} | {3,2} | {4,2} | {5,2} | ... | {∞,2} |
| Coxeter diagram |
... | ||||||
| Faces | 2 {1} | 2 {2} | 2 {3} | 2 {4} | 2 {5} | ... | 2 {∞} |
| Edges and vertices |
1 | 2 | 3 | 4 | 5 | ... | ∞ |
| Vertex config. |
1.1 | 2.2 | 3.3 | 4.4 | 5.5 | ... | ∞.∞ |
Relation to tilings of the projective plane
[edit]Spherical polyhedra having at least one inversive symmetry are related to projective polyhedra[4] (tessellations of the real projective plane) – just as the sphere has a 2-to-1 covering map of the projective plane, projective polyhedra correspond under 2-fold cover to spherical polyhedra that are symmetric under reflection through the origin.
The best-known examples of projective polyhedra are the regular projective polyhedra, the quotients of the centrally symmetric Platonic solids, as well as two infinite classes of even dihedra and hosohedra:[5]
- Hemi-cube, {4,3}/2
- Hemi-octahedron, {3,4}/2
- Hemi-dodecahedron, {5,3}/2
- Hemi-icosahedron, {3,5}/2
- Hemi-dihedron, {2p,2}/2, p>=1
- Hemi-hosohedron, {2,2p}/2, p>=1
See also
[edit]- Spherical geometry
- Spherical trigonometry
- Polyhedron
- Projective polyhedron
- Toroidal polyhedron
- Conway polyhedron notation
References
[edit]- ^ Sarhangi, Reza (September 2008). "Illustrating Abu al-Wafā' Būzjānī: Flat images, spherical constructions". Iranian Studies. 41 (4): 511–523. doi:10.1080/00210860802246184.
- ^ Popko, Edward S. (2012). Divided Spheres: Geodesics and the Orderly Subdivision of the Sphere. CRC Press. p. xix. ISBN 978-1-4665-0430-1.
Buckminster Fuller's invention of the geodesic dome was the biggest stimulus for spherical subdivision research and development.
- ^ Coxeter, H.S.M.; Longuet-Higgins, M.S.; Miller, J.C.P. (1954). "Uniform polyhedra". Phil. Trans. 246 A (916): 401–50. JSTOR 91532.
- ^ McMullen, Peter; Schulte, Egon (2002). "6C. Projective Regular Polytopes". Abstract Regular Polytopes. Cambridge University Press. pp. 162–5. ISBN 0-521-81496-0.
- ^ Coxeter, H.S.M. (1969). "§21.3 Regular maps'". Introduction to Geometry (2nd ed.). Wiley. pp. 386–8. ISBN 978-0-471-50458-0. MR 0123930.


