Regular skew apeirohedron

In geometry, a regular skew apeirohedron is an infinite regular skew polyhedron. They have either skew regular faces or skew regular vertex figures.
History
[edit]In 1926 John Flinders Petrie took the concept of a regular skew polygons, polygons whose vertices are not all in the same plane, and extended it to polyhedra. While apeirohedra are typically required to tile the 2-dimensional plane, Petrie considered cases where the faces were still convex but were not required to lie flat in the plane, they could have a skew polygon vertex figure.
Petrie discovered two regular skew apeirohedra, the mucube and the muoctahedron.[1] Harold Scott MacDonald Coxeter derived a third, the mutetrahedron, and proved that the these three were complete. Under Coxeter and Petrie's definition, requiring convex faces and allowing a skew vertex figure, the three were not only the only skew apeirohedra in 3-dimensional Euclidean space, but they were the only skew polyhedra in 3-space as there Coxeter showed there were no finite cases.
In 1967[2] Garner investigated regular skew apeirohedra in hyperbolic 3-space with Petrie and Coxeters definition, discovering 31[note 1] regular skew apeirohedra with compact or paracompact symmetry.
In 1977[3][1] Grünbaum generalized skew polyhedra to allow for skew faces as well. Grünbaum discovered an additional 23[note 2] skew apeirohedra in 3-dimensional Euclidean space and 3 in 2-dimensional space which are skew by virtue of their faces. 12 of Grünbaum's polyhedra were formed using the blending operation on 2-dimensional apeirohedra, and the other 11 were pure, i.e. could not be formed by a non-trivial blend. Grünbaum conjectured that this new list was complete for the parameters considered.
In 1985[4][1] Dress found an additional pure regular skew apeirohedron in 3-space, and proved that with this additional skew apeirohedron the list was complete.
Regular skew apeirohedra in Euclidean 3-space
[edit]Petrie-Coxeter polyhedra
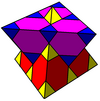
[edit]The three Euclidean solutions in 3-space are {4,6|4}, {6,4|4}, and {6,6|3}. John Conway named them mucube, muoctahedron, and mutetrahedron respectively for multiple cube, octahedron, and tetrahedron.[5]
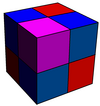
- Mucube: {4,6|4}: 6 squares about each vertex (related to cubic honeycomb, constructed by cubic cells, removing two opposite faces from each, and linking sets of six together around a faceless cube.)
- Muoctahedron: {6,4|4}: 4 hexagons about each vertex (related to bitruncated cubic honeycomb, constructed by truncated octahedron with their square faces removed and linking hole pairs of holes together.)
- Mutetrahedron: {6,6|3}: 6 hexagons about each vertex (related to quarter cubic honeycomb, constructed by truncated tetrahedron cells, removing triangle faces, and linking sets of four around a faceless tetrahedron.)
Coxeter gives these regular skew apeirohedra {2q,2r|p} with extended chiral symmetry [[(p,q,p,r)]+] which he says is isomorphic to his abstract group (2q,2r|2,p). The related honeycomb has the extended symmetry [[(p,q,p,r)]].[6]
| Coxeter group symmetry |
Apeirohedron {p,q|l} |
Image | Face {p} |
Hole {l} |
Vertex figure |
Related honeycomb | |
|---|---|---|---|---|---|---|---|
[[4,3,4]] [[4,3,4]+] |
{4,6|4} Mucube |
 animation |
 |
 |
 |
t0,3{4,3,4} |
|
| {6,4|4} Muoctahedron |
 animation |
 |
 |
2t{4,3,4} |

| ||
[[3[4]]] [[3[4]]+] |
{6,6|3} Mutetrahedron |
 animation |
 |
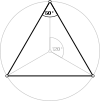 |
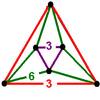 |
q{4,3,4} |
|
Grünbaum-Dress polyhedra
[edit]Skew honeycombs
[edit]There are 3 regular skew apeirohedra of full rank, also called regular skew honeycombs, that is skew apeirohedra in 2-dimensions. As with the finite skew polyhedra of full rank, all three of these can be obtained by applying the Petrie dual to planar polytopes, in this case the three regular tilings.[7][8][9]
Alternatively they can be constructed using the apeir operation on regular polygons.[10] While the Petrial is used the classical construction, it does not generalize well to higher ranks. In contrast, the apeir operation is used to construct higher rank skew honeycombs.[11]
The apeir operation takes the generating mirrors of the polygon, ρ0 and ρ1, and uses them as the mirrors for the vertex figure of a polyhedron, the new vertex mirror w is then a point located where the initial vertex of the polygon (or anywhere on the mirror ρ1 other than its intersection with ρ0). The new initial vertex is placed at the intersection of the mirrors ρ0 and ρ1. Thus the apeir polyhedron is generated by ⟨w, ρ0, ρ0⟩.[12]
| Skew honeycombs | Schläfli symbol | Faces | Image | Petrie dual | Apeir of | ||
|---|---|---|---|---|---|---|---|
| Petrial square tiling | {4,4}π | {∞,4}4 | ∞ zigzags |  |
Square tiling | Square | 
|
| Petrial triangular tiling | {3,6}π | {∞,6}3 | ∞ zigzags |  |
Triangular tiling | Hexagon | 
|
| Petrial hexagonal tiling | {6,3}π | {∞,3}6 | ∞ zigzags |  |
Hexagonal tiling | Triangle | 
|
Blended apeirohedra
[edit]
For any two regular polytopes, P and Q, a new polytope can be made by the following process:
- Start with the Cartesian product of the vertices of P with the vertices of Q.
- Add edges between any two vertices p0 × q0 and p1 × q1 iff there is an edge between p0 and p1 in P and an edge between q0 and q1 in Q. (If Q has no edges then add a virtual edge connecting its vertex to itself.)
- Similarly add faces to every set of vertices all incident on the same face in both P and Q. (If Q has no faces then add a virtual face connecting its edge to itself.)
- Repeat as such for all ranks of proper elements.
- From the resulting polytope, select one connected component.
For regular polytopes the last step is guaranteed to produce a unique result. This new polytope is called the blend of P and Q and is represented P#Q.
Equivalently the blend can be obtained by positioning P and Q in orthogonal spaces and taking composing their generating mirrors pairwise.
Blended polyhedra in 3-dimensional space can be made by blending 2-dimensional polyhedra with 1-dimensional polytopes. The only 2-dimensional polyhedra are the 6 honeycombs (3 Euclidean tilings and 3 skew honeycombs):
- Triangular tiling: {3, 6}
- Square tiling: {4, 4}
- Hexagonal tiling: {6, 3}
- Petrial triangular tiling: {3, 6}π
- Petrial square tiling: {4, 4}π
- Petrial hexagonal tiling: {6, 3}π
The only 1-dimensional polytopes are:
- The line segment: {}
- The apeirogon: {∞}
Each pair between these produces a valid distinct regular skew apeirohedron in 3-dimensional Euclidean space, for a total of 12[note 2] blended skew apeirohedra.
Since the skeleton of the square tiling is bipartite, two of these blends, {4, 4}#{} and {4, 4}π#{}, are combinatrially equivalent to their non-blended counterparts.
Pure apeirohedra
[edit]
- π represents the Petrial
- δ represents the dual
- η represents halving
- φ represents facetting
- σ represents skewing
- r represents rectification
This section needs expansion. You can help by adding to it. (February 2024) |
A polytope is considered pure if it cannot be expressed as a non-trivial blend of two polytopes. A blend is considered trivial if it contains the result as one of the components. Alternatively a pure polytope is one whose symmetry group contains no non-trivial subrepresentation.[13]
There are 12 regular pure apeirohedra in 3 dimensions. Three of these are the Petrie-Coxeter polyhedra:
- {4,6 | 4}
- {6,4 | 4}
- {6,6 | 3}
Three more are obtained as the Petrials of the Petrie-Coxeter polyhedra:
- {4,6 | 4}π = {∞, 4}6,4
- {6,4 | 4}π = {∞, 6}4,4
- {6,6 | 3}π = {∞, 6}6,3
Three additional pure apeirohedra can be formed with finite skew polygons as faces:
These 3 are closed under the Wilson operations. Meaning that each can be constructed from any other by some combination of the Petrial and dual operations. {6,6}4 is self-dual and {6,4}6 is self-Petrial.
Regular skew apeirohedra in hyperbolic 3-space
[edit]
In 1967, C. W. L. Garner identified 31 hyperbolic skew apeirohedra with regular skew polygon vertex figures, found by extending the Petrie-Coxeter polyhedra to hyperbolic space.[14]
These represent 14 compact and 17[note 1] paracompact regular skew polyhedra in hyperbolic space, constructed from the symmetry of a subset of linear and cyclic Coxeter groups graphs of the form [[(p,q,p,r)]], These define regular skew polyhedra {2q,2r|p} and dual {2r,2q|p}. For the special case of linear graph groups r = 2, this represents the Coxeter group [p,q,p]. It generates regular skews {2q,4|p} and {4,2q|p}. All of these exist as a subset of faces of the convex uniform honeycombs in hyperbolic space.
The skew apeirohedron shares the same antiprism vertex figure with the honeycomb, but only the zig-zag edge faces of the vertex figure are realized, while the other faces make holes.
| Coxeter group |
Apeirohedron {p,q|l} |
Face {p} |
Hole {l} |
Honeycomb | Vertex figure |
Apeirohedron {p,q|l} |
Face {p} |
Hole {l} |
Honeycomb | Vertex figure | |
|---|---|---|---|---|---|---|---|---|---|---|---|
[3,5,3] |
{10,4|3} |  |
 |
2t{3,5,3} |
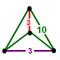 |
{4,10|3} |  |
 |
t0,3{3,5,3} |
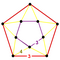
| |
[5,3,5] |
{6,4|5} |  |
 |
2t{5,3,5} |
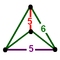 |
{4,6|5} |  |
 |
t0,3{5,3,5} |
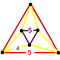
| |
[(4,3,3,3)] |
{8,6|3} |  |
 |
ct{(4,3,3,3)} |
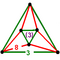 |
{6,8|3} |  |
 |
ct{(3,3,4,3)} |
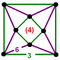
| |
[(5,3,3,3)] |
{10,6|3} |  |
 |
ct{(5,3,3,3)} |
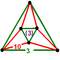 |
{6,10|3} |  |
 |
ct{(3,3,5,3)} |

| |
[(4,3,4,3)] |
{8,8|3} |  |
 |
ct{(4,3,4,3)} |
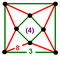 |
{6,6|4} |  |
 |
ct{(3,4,3,4)} |
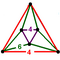
| |
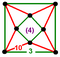
[(5,3,4,3)] |
{8,10|3} |  |
 |
ct{(4,3,5,3)} |
 |
{10,8|3} |  |
 |
ct{(5,3,4,3)} |

| |
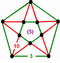
[(5,3,5,3)] |
{10,10|3} |  |
 |
ct{(5,3,5,3)} |
 |
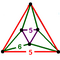
{6,6|5} |  |
 |
ct{(3,5,3,5)} |
|
| Coxeter group |
Apeirohedron {p,q|l} |
Face {p} |
Hole {l} |
Honeycomb | Vertex figure |
Apeirohedron {p,q|l} |
Face {p} |
Hole {l} |
Honeycomb | Vertex figure | |
|---|---|---|---|---|---|---|---|---|---|---|---|
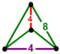
[4,4,4] |
{8,4|4} |  |
 |
2t{4,4,4} |
 |
{4,8|4} |  |
 |
t0,3{4,4,4} |

| |
[3,6,3] |
{12,4|3} | 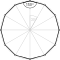 |
 |
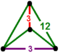
2t{3,6,3} |
 |
{4,12|3} |  |
 |
t0,3{3,6,3} |
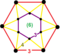
| |
[6,3,6] |
{6,4|6} |  |
 |
2t{6,3,6} |
 |
{4,6|6} |  |
 |
t0,3{6,3,6} |

| |
[(4,4,4,3)] |
{8,6|4} |  |
 |
ct{(4,4,3,4)} |
 |
{6,8|4} |  |
 |
ct{(3,4,4,4)} |

| |
[(4,4,4,4)] |
{8,8|4} |  |
 |
q{4,4,4} |

| ||||||
[(6,3,3,3)] |
{12,6|3} |  |
 |
ct{(6,3,3,3)} |
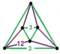 |
{6,12|3} |  |
 |
ct{(3,3,6,3)} |

| |
[(6,3,4,3)] |
{12,8|3} |  |
 |
ct{(6,3,4,3)} |
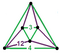 |
{8,12|3} |  |
 |
ct{(4,3,6,3)} |

| |
[(6,3,5,3)] |
{12,10|3} |  |
 |
ct{(6,3,5,3)} |
 |
{10,12|3} |  |
 |
ct{(5,3,6,3)} |

| |
[(6,3,6,3)] |
{12,12|3} |  |
 |
ct{(6,3,6,3)} |
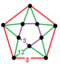 |
{6,6|6} |  |
 |
ct{(3,6,3,6)} |
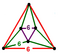
|
See also
[edit]Notes
[edit]- ^ Jump up to: a b Garner mistakenly counts {8,8|4} twice giving a count of 18 paracompact cases and 32 total, but only listing 17 paracompact and 31 total.
- ^ Jump up to: a b Polytopes produced as a non-trivial blend have a degree of freedom corresponding to the relative scaling of their components. For this reason some authors count these as infinite families rather than a single polytope. This article counts two polytopes as equal when there is an affine map of full rank between them.
References
[edit]- ^ Jump up to: a b c McMullen & Schulte (1997:449–450)
- ^ Garner (1967)
- ^ Grünbaum (1977)
- ^ Dress (1985)
- ^ The Symmetry of Things, 2008, Chapter 23 Objects with Primary Symmetry, Infinite Platonic Polyhedra, pp. 333–335
- ^ Coxeter, Regular and Semi-Regular Polytopes II 2.34)
- ^ Grünbaum (1977)
- ^ Dress (1985)
- ^ McMullen & Schulte (1997)
- ^ McMullen (2004)
- ^ McMullen (2004)
- ^ McMullen (2004)
- ^ McMullen & Schulte (2002)
- ^ Garner (1967)
Bibliography
[edit]- Garner (1967), "Regular Skew Polyhedra in Hyperbolic Three-Space", Canadian Journal of Mathematics, 19: 1179–1186, doi:10.4153/CJM-1967-106-9
- Grünbaum, Branko (1977), "Regular polyhedra - old and new" (PDF), Aequationes Mathematicae, 16 (1–2): 1–20, doi:10.1007/BF01836414, S2CID 125049930
- McMullen, Peter; Schulte, Egon (1997). "Regular Polytopes in Ordinary Space" (PDF). Discrete & Computational Geometry. 17 (47): 449–478. doi:10.1007/PL00009304.
- McMullen, Peter; Schulte, Egon (2002), Abstract Regular Polytopes, Encyclopedia of Mathematics and its Applications, vol. 92, Cambridge: Cambridge University Press, doi:10.1017/CBO9780511546686, ISBN 0-521-81496-0, MR 1965665
- McMullen, Peter (2004). "Regular Polytopes of Full Rank" (PDF). Discrete Computational Geometry. 32: 1–35. doi:10.1007/s00454-004-0848-5.
- Dress, Andreas (1985). "A combinatorial theory of Grünbaum's new regular polyhedra, Part II: Complete enumeration". Aequationes Mathematicae. 29: 222–243. doi:10.1007/BF02189831. S2CID 121260389.
- Petrie–Coxeter Maps Revisited PDF, Isabel Hubard, Egon Schulte, Asia Ivic Weiss, 2005
- John H. Conway, Heidi Burgiel, Chaim Goodman-Strauss, The Symmetries of Things 2008, ISBN 978-1-56881-220-5,
- Peter McMullen, Four-Dimensional Regular Polyhedra, Discrete & Computational Geometry September 2007, Volume 38, Issue 2, pp 355–387
- Coxeter, Regular Polytopes, Third edition, (1973), Dover edition, ISBN 0-486-61480-8
- Kaleidoscopes: Selected Writings of H.S.M. Coxeter, edited by F. Arthur Sherk, Peter McMullen, Anthony C. Thompson, Asia Ivic Weiss, Wiley-Interscience Publication, 1995, ISBN 978-0-471-01003-6 [1]
- (Paper 2) H.S.M. Coxeter, "The Regular Sponges, or Skew Polyhedra", Scripta Mathematica 6 (1939) 240–244.
- (Paper 22) H.S.M. Coxeter, Regular and Semi Regular Polytopes I, [Math. Zeit. 46 (1940) 380–407, MR 2,10]
- (Paper 23) H.S.M. Coxeter, Regular and Semi-Regular Polytopes II, [Math. Zeit. 188 (1985) 559–591]
- Coxeter, The Beauty of Geometry: Twelve Essays, Dover Publications, 1999, ISBN 0-486-40919-8 (Chapter 5: Regular Skew Polyhedra in three and four dimensions and their topological analogues, Proceedings of the London Mathematics Society, Ser. 2, Vol 43, 1937.)
- Coxeter, H. S. M. Regular Skew Polyhedra in Three and Four Dimensions. Proc. London Math. Soc. 43, 33–62, 1937.



