Lists of uniform tilings on the sphere, plane, and hyperbolic plane

In geometry, many uniform tilings on sphere, euclidean plane, and hyperbolic plane can be made by Wythoff construction within a fundamental triangle, (p q r), defined by internal angles as π/p, π/q, and π/r. Special cases are right triangles (p q 2). Uniform solutions are constructed by a single generator point with 7 positions within the fundamental triangle, the 3 corners, along the 3 edges, and the triangle interior. All vertices exist at the generator, or a reflected copy of it. Edges exist between a generator point and its image across a mirror. Up to 3 face types exist centered on the fundamental triangle corners. Right triangle domains can have as few as 1 face type, making regular forms, while general triangles have at least 2 triangle types, leading at best to a quasiregular tiling.

There are different notations for expressing these uniform solutions, Wythoff symbol, Coxeter diagram, and Coxeter's t-notation.

Simple tiles are generated by Möbius triangles with whole numbers p,q,r, while Schwarz triangles allow rational numbers p,q,r and allow star polygon faces, and have overlapping elements.

7 generator points

The seven generator points with each set of $p,q,r$ (and a few special forms):

General				Right triangle (r=2)
Description	Wythoff symbol	Vertex configuration	Coxeter diagram	Wythoff symbol	Vertex configuration	Schläfli symbol		Coxeter diagram
regular and quasiregular	$q \| p r$	$(p . r) q$		$q \| p 2$	$p q$	{p,q}
	$p \| q r$	$(q . r) p$		$p \| q 2$	$q p$	{q,p}
	$r \| p q$	$(q . p) r$		$2 \| p q$	$(q . p)²$	r{p,q}	t₁{p,q}
truncated and expanded	$q r \| p$	⁠ $q.2p.r.2p$ ⁠		$q 2 \| p$	⁠ $q.2p.2p$ ⁠	t{p,q}	t_0,1{p,q}
	$p r \| q$	⁠ $p.2q.r.2q$ ⁠		$p 2 \| q$	$p . 2 q .2 q$	t{q,p}	t_0,1{q,p}
	$p q \| r$	⁠ $2r.q.2r.p$ ⁠		$p q \| 2$	⁠ $4.q.4.p$ ⁠	rr{p,q}	t_0,2{p,q}
even-faced	$p q r \|$	⁠ $2r.2q.2p$ ⁠		$p q 2 \|$	⁠ $4.2q.2p$ ⁠	tr{p,q}	t_0,1,2{p,q}
even-faced	$p q (r s) \|$	⁠ $2p.2q.-2p.-2q$ ⁠	-	$p 2 (r s) \|$	$2 p .4.-2 p . 4 / 3$			-
snub	$\| p q r$	⁠ $3.r.3.q.3.p$ ⁠		$\| p q 2$	⁠ $3.3.q.3.p$ ⁠	sr{p,q}
snub	$\| p q r s$	⁠ $(4.p.4.q.4.r.4.s)/2$ ⁠	-	-	-			-

There are three special cases:

$p\ q\ (r\ s)\ |$ – This is a mixture of $p\ q\ r\ |$ and $p\ q\ s\ |$ , containing only the faces shared by both.
$|\ p\ q\ r$ – Snub forms (alternated) are given by this otherwise unused symbol.
$|\ p\ q\ r\ s$ – A unique snub form for U75 that isn't Wythoff-constructible.

Symmetry triangles

There are 4 symmetry classes of reflection on the sphere, and three in the Euclidean plane. A few of the infinitely many such patterns in the hyperbolic plane are also listed. (Increasing any of the numbers defining a hyperbolic or Euclidean tiling makes another hyperbolic tiling.)

Point groups:

(p 2 2) dihedral symmetry, $p=2,3,4\dots$ (order $4p$ )
(3 3 2) tetrahedral symmetry (order 24)
(4 3 2) octahedral symmetry (order 48)
(5 3 2) icosahedral symmetry (order 120)

Euclidean (affine) groups:

(4 4 2) *442 symmetry: 45°-45°-90° triangle
(6 3 2) *632 symmetry: 30°-60°-90° triangle
(3 3 3) *333 symmetry: 60°-60°-60° triangle

Hyperbolic groups:

(7 3 2) *732 symmetry
(8 3 2) *832 symmetry
(4 3 3) *433 symmetry
(4 4 3) *443 symmetry
(4 4 4) *444 symmetry
(5 4 2) *542 symmetry
(6 4 2) *642 symmetry
...

Dihedral spherical					Spherical
D_2h	D_3h	D_4h	D_5h	D_6h	T_d	O_h	I_h
*222	*322	*422	*522	*622	*332	*432	*532
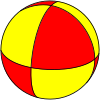(2 2 2)	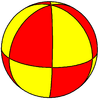(3 2 2)	(4 2 2)	(5 2 2)	(6 2 2)	(3 3 2)	(4 3 2)	(5 3 2)

The above symmetry groups only include the integer solutions on the sphere. The list of Schwarz triangles includes rational numbers, and determine the full set of solutions of nonconvex uniform polyhedra.

Euclidean plane
p4m	p3m	p6m
*442	*333	*632
(4 4 2)	(3 3 3)	(6 3 2)

Hyperbolic plane
*732	*542	*433
(7 3 2)	(5 4 2)	(4 3 3)

In the tilings above, each triangle is a fundamental domain, colored by even and odd reflections.

Summary spherical, Euclidean and hyperbolic tilings

Selected tilings created by the Wythoff construction are given below.

Spherical tilings (r = 2)

(p q 2)	Parent	Truncated	Rectified	Bitruncated	Birectified (dual)	Cantellated	Omnitruncated (Cantitruncated)	Snub
Wythoff symbol	q \| p 2	2 q \| p	2 \| p q	2 p \| q	p \| q 2	p q \| 2	p q 2 \|	\| p q 2
Schläfli symbol	${\begin{Bmatrix}p,q\end{Bmatrix}}$	$t{\begin{Bmatrix}p,q\end{Bmatrix}}$	${\begin{Bmatrix}p\\q\end{Bmatrix}}$	$t{\begin{Bmatrix}q,p\end{Bmatrix}}$	${\begin{Bmatrix}q,p\end{Bmatrix}}$	$r{\begin{Bmatrix}p\\q\end{Bmatrix}}$	$t{\begin{Bmatrix}p\\q\end{Bmatrix}}$	$s{\begin{Bmatrix}p\\q\end{Bmatrix}}$
	{p,q}	t{p,q}	r{p,q}	t{q,p}	{q,p}	rr{p,q}	tr{p,q}	sr{p,q}
	t₀{p,q}	t_0,1{p,q}	t₁{p,q}	t_1,2{p,q}	t₂{p,q}	t_0,2{p,q}	t_0,1,2{p,q}	sr{p,q}
Coxeter diagram
Vertex figure	p^q	q.2p.2p	(p.q)²	p. 2q.2q	q^p	p. 4.q.4	4.2p.2q	3.3.p. 3.q
(3 3 2)	{3,3}	(3.6.6)	(3.3a.3.3a)	(3.6.6)	{3,3}	(3a.4.3b.4)	(4.6a.6b)	(3.3.3a.3.3b)
(4 3 2)	{4,3}	(3.8.8)	(3.4.3.4)	(4.6.6)	{3,4}	(3.4.4a.4)	(4.6.8)	(3.3.3a.3.4)
(5 3 2)	{5,3}	(3.10.10)	(3.5.3.5)	(5.6.6)	{3,5}	(3.4.5.4)	(4.6.10)	(3.3.3a.3.5)

Some overlapping spherical tilings (r = 2)

Tilings are shown as polyhedra. Some of the forms are degenerate, given with brackets for vertex figures, with overlapping edges or vertices.

(p q 2)	Parent	Truncated	Rectified	Bitruncated	Birectified (dual)	Cantellated	Omnitruncated (Cantitruncated)	Snub
Wythoff symbol	q \| p 2	2 q \| p	2 \| p q	2 p \| q	p \| q 2	p q \| 2	p q 2 \|	\| p q 2
Schläfli symbol	${\begin{Bmatrix}p,q\end{Bmatrix}}$	$t{\begin{Bmatrix}p,q\end{Bmatrix}}$	${\begin{Bmatrix}p\\q\end{Bmatrix}}$	$t{\begin{Bmatrix}q,p\end{Bmatrix}}$	${\begin{Bmatrix}q,p\end{Bmatrix}}$	$r{\begin{Bmatrix}p\\q\end{Bmatrix}}$	$t{\begin{Bmatrix}p\\q\end{Bmatrix}}$	$s{\begin{Bmatrix}p\\q\end{Bmatrix}}$
	{p,q}	t{p,q}	r{p,q}	t{q,p}	{q,p}	rr{p,q}	tr{p,q}	sr{p,q}
	t₀{p,q}	t_0,1{p,q}	t₁{p,q}	t_1,2{p,q}	t₂{p,q}	t_0,2{p,q}	t_0,1,2{p,q}	sr{p,q}
Coxeter–Dynkin diagram
Vertex figure	p^q	(q.2p.2p)	(p.q.p.q)	(p. 2q.2q)	q^p	(p. 4.q.4)	(4.2p.2q)	(3.3.p. 3.q)
Icosahedral (5/2 3 2)	{3,5/2}	(5/2.6.6)	(3.5/2)²	[3.10/2.10/2]	{5/2,3}	[3.4.5/2.4]	[4.10/2.6]	(3.3.3.3.5/2)
Icosahedral (5 5/2 2)	{5,5/2}	(5/2.10.10)	(5/2.5)²	[5.10/2.10/2]	{5/2,5}	(5/2.4.5.4)	[4.10/2.10]	(3.3.5/2.3.5)

Dihedral symmetry (q = r = 2)

Spherical tilings with dihedral symmetry exist for all $p=2,3,4,\dots$ many with digon faces which become degenerate polyhedra. Two of the eight forms (Rectified and cantillated) are replications and are skipped in the table.

(p 2 2) Fundamental domain	Parent	Truncated	Bitruncated (truncated dual)	Birectified (dual)	Omnitruncated (Cantitruncated)	Snub
Extended Schläfli symbol	${\begin{Bmatrix}p,2\end{Bmatrix}}$	$t{\begin{Bmatrix}p,2\end{Bmatrix}}$	$t{\begin{Bmatrix}2,p\end{Bmatrix}}$	${\begin{Bmatrix}2,p\end{Bmatrix}}$	$t{\begin{Bmatrix}p\\2\end{Bmatrix}}$	$s{\begin{Bmatrix}p\\2\end{Bmatrix}}$
	{p,2}	t{p,2}	t{2,p}	{2,p}	tr{p,2}	sr{p,2}
	t₀{p,2}	t_0,1{p,2}	t_1,2{p,2}	t₂{p,2}	t_0,1,2{p,2}	sr{p,2}
Wythoff symbol	2 \| p 2	2 2 \| p	2 p \| 2	p \| 2 2	p 2 2 \|	\| p 2 2
Coxeter–Dynkin diagram
Vertex figure	p²	(2.2p.2p)	(4.4.p)	2^p	(4.2p.4)	(3.3.p. 3)
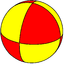(2 2 2) V2.2.2	{2,2}	2.4.4	4.4.2	{2,2}	4.4.4	3.3.3.2
(3 2 2) V3.2.2	{3,2}	2.6.6	4.4.3	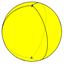{2,3}	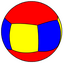4.4.6	3.3.3.3
(4 2 2) V4.2.2	{4,2}	2.8.8	4.4.4	{2,4}	4.4.8	3.3.3.4
(5 2 2) V5.2.2	{5,2}	2.10.10	4.4.5	{2,5}	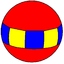4.4.10	3.3.3.5
(6 2 2) V6.2.2	{6,2}	2.12.12	4.4.6	{2,6}	4.4.12	3.3.3.6
...

Euclidean and hyperbolic tilings (r = 2)

Some representative hyperbolic tilings are given, and shown as a Poincaré disk projection.

(p q 2)	Fund. triangles	Parent	Truncated	Rectified	Bitruncated	Birectified (dual)	Cantellated	Omnitruncated (Cantitruncated)	Snub
Wythoff symbol		q \| p 2	2 q \| p	2 \| p q	2 p \| q	p \| q 2	p q \| 2	p q 2 \|	\| p q 2
Schläfli symbol		${\begin{Bmatrix}p,q\end{Bmatrix}}$	$t{\begin{Bmatrix}p,q\end{Bmatrix}}$	${\begin{Bmatrix}p\\q\end{Bmatrix}}$	$t{\begin{Bmatrix}q,p\end{Bmatrix}}$	${\begin{Bmatrix}q,p\end{Bmatrix}}$	$r{\begin{Bmatrix}p\\q\end{Bmatrix}}$	$t{\begin{Bmatrix}p\\q\end{Bmatrix}}$	$s{\begin{Bmatrix}p\\q\end{Bmatrix}}$
		{p,q}	t{p,q}	r{p,q}	t{q,p}	{q,p}	rr{p,q}	tr{p,q}	sr{p,q}
		t₀{p,q}	t_0,1{p,q}	t₁{p,q}	t_1,2{p,q}	t₂{p,q}	t_0,2{p,q}	t_0,1,2{p,q}	sr{p,q}
Coxeter–Dynkin diagram
Vertex figure		p^q	(q.2p.2p)	(p.q.p.q)	(p. 2q.2q)	q^p	(p. 4.q.4)	(4.2p.2q)	(3.3.p. 3.q)
Hexagonal tiling (6 3 2)	V4.6.12	{6,3}	3.12.12	3.6.3.6	6.6.6	{3,6}	3.4.6.4	4.6.12	3.3.3.3.6
(Hyperbolic plane) (7 3 2)	V4.6.14	{7,3}	3.14.14	3.7.3.7	7.6.6	{3,7}	3.4.7.4	4.6.14	3.3.3.3.7
(Hyperbolic plane) (8 3 2)	V4.6.16	{8,3}	3.16.16	3.8.3.8	8.6.6	{3,8}	3.4.8.4	4.6.16	3.3.3.3.8
Square tiling (4 4 2)	V4.8.8	{4,4}	4.8.8	4.4a.4.4a	4.8.8	{4,4}	4.4a.4b.4a	4.8.8	3.3.4a.3.4b
(Hyperbolic plane) (5 4 2)	V4.8.10	{5,4}	4.10.10	4.5.4.5	5.8.8	{4,5}	4.4.5.4	4.8.10	3.3.4.3.5
(Hyperbolic plane) (6 4 2)	V4.8.12	{6,4}	4.12.12	4.6.4.6	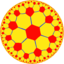6.8.8	{4,6}	4.4.6.4	4.8.12	3.3.4.3.6
(Hyperbolic plane) (7 4 2)	V4.8.14	{7,4}	4.14.14	4.7.4.7	7.8.8	{4,7}	4.4.7.4	4.8.14	3.3.4.3.7
(Hyperbolic plane) (8 4 2)	V4.8.16	{8,4}	4.16.16	4.8.4.8	8.8.8	{4,8}	4.4.8.4	4.8.16	3.3.4.3.8
(Hyperbolic plane) (5 5 2)	V4.10.10	{5,5}	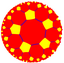5.10.10	5.5.5.5	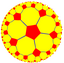5.10.10	{5,5}	5.4.5.4	4.10.10	3.3.5.3.5
(Hyperbolic plane) (6 5 2)	V4.10.12	{6,5}	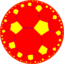5.12.12	5.6.5.6	6.10.10	{5,6}	5.4.6.4	4.10.12	3.3.5.3.6
(Hyperbolic plane) (7 5 2)	V4.10.14	{7,5}	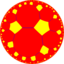5.14.14	5.7.5.7	7.10.10	{5,7}	5.4.7.4	4.10.14	3.3.5.3.7
(Hyperbolic plane) (8 5 2)	V4.10.16	{8,5}	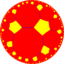5.16.16	5.8.5.8	8.10.10	{5,8}	5.4.8.4	4.10.16	3.3.5.3.8
(Hyperbolic plane) (6 6 2)	V4.12.12	{6,6}	6.12.12	6.6.6.6	6.12.12	{6,6}	6.4.6.4	4.12.12	3.3.6.3.6
(Hyperbolic plane) (7 6 2)	V4.12.14	{7,6}	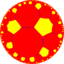6.14.14	6.7.6.7	7.12.12	{6,7}	6.4.7.4	4.12.14	3.3.6.3.7
(Hyperbolic plane) (8 6 2)	V4.12.16	{8,6}	6.16.16	6.8.6.8	8.12.12	{6,8}	6.4.8.4	4.12.16	3.3.6.3.8
(Hyperbolic plane) (7 7 2)	V4.14.14	{7,7}	7.14.14	7.7.7.7	7.14.14	{7,7}	7.4.7.4	4.14.14	3.3.7.3.7
(Hyperbolic plane) (8 7 2)	V4.14.16	{8,7}	7.16.16	7.8.7.8	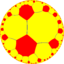8.14.14	{7,8}	7.4.8.4	4.14.16	3.3.7.3.8
(Hyperbolic plane) (8 8 2)	V4.16.16	{8,8}	8.16.16	8.8.8.8	8.16.16	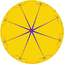{8,8}	8.4.8.4	4.16.16	3.3.8.3.8
(Hyperbolic plane) (∞ 3 2)	V4.6.∞	{∞,3}	3.∞.∞	3.∞.3.∞	∞.6.6	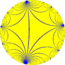{3,∞}	3.4.∞.4	4.6.∞	3.3.3.3.∞
(Hyperbolic plane) (∞ 4 2)	V4.8.∞	{∞,4}	4.∞.∞	4.∞.4.∞	∞.8.8	{4,∞}	4.4.∞.4	4.8.∞	3.3.4.3.∞
(Hyperbolic plane) (∞ 5 2)	V4.10.∞	{∞,5}	5.∞.∞	5.∞.5.∞	∞.10.10	{5,∞}	5.4.∞.4	4.10.∞	3.3.5.3.∞
(Hyperbolic plane) (∞ 6 2)	V4.12.∞	{∞,6}	6.∞.∞	6.∞.6.∞	∞.12.12	{6,∞}	6.4.∞.4	4.12.∞	3.3.6.3.∞
(Hyperbolic plane) (∞ 7 2)	V4.14.∞	{∞,7}	7.∞.∞	7.∞.7.∞	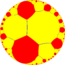∞.14.14	{7,∞}	7.4.∞.4	4.14.∞	3.3.7.3.∞
(Hyperbolic plane) (∞ 8 2)	V4.16.∞	{∞,8}	8.∞.∞	8.∞.8.∞	∞.16.16	{8,∞}	8.4.∞.4	4.16.∞	3.3.8.3.∞
(Hyperbolic plane) (∞ ∞ 2)	V4.∞.∞	{∞,∞}	∞.∞.∞	∞.∞.∞.∞	∞.∞.∞	{∞,∞}	∞.4.∞.4	4.∞.∞	3.3.∞.3.∞

Euclidean and hyperbolic tilings (r > 2)

The Coxeter–Dynkin diagram is given in a linear form, although it is actually a triangle, with the trailing segment r connecting to the first node.

Wythoff symbol (p q r)	Fund. triangles	q \| p r	r q \| p	r \| p q	r p \| q	p \| q r	p q \| r	p q r \|	\| p q r
Schläfli symbol		(p,q,r)	r(r,q,p)	(q,r,p)	r(p,q,r)	(q,p,r)	r(p,r,q)	tr(p,q,r)	s(p,q,r)
Schläfli symbol		t₀(p,q,r)	t_0,1(p,q,r)	t₁(p,q,r)	t_1,2(p,q,r)	t₂(p,q,r)	t_0,2(p,q,r)	t_0,1,2(p,q,r)	s(p,q,r)
Coxeter diagram
Vertex figure		(p.r)^q	(r.2p.q.2p)	(p.q)^r	(r.2q.p. 2q)	(q.r)^p	(p. 2r.q.2r)	(2p.2q.2r)	(3.r.3.q.3.p)
Euclidean (3 3 3)	V6.6.6	(3.3)³	3.6.3.6	(3.3)³	3.6.3.6	(3.3)³	3.6.3.6	6.6.6	3.3.3.3.3.3
Hyperbolic (4 3 3)	V6.6.8	(3.4)³	3.8.3.8	(3.4)³	3.6.4.6	(3.3)⁴	3.6.4.6	6.6.8	3.3.3.3.3.4
Hyperbolic (4 4 3)	V6.8.8	(3.4)⁴	3.8.4.8	(4.4)³	3.8.4.8	(3.4)⁴	4.6.4.6	6.8.8	3.3.3.4.3.4
Hyperbolic (4 4 4)	V8.8.8	(4.4)⁴	4.8.4.8	(4.4)⁴	4.8.4.8	(4.4)⁴	4.8.4.8	8.8.8	3.4.3.4.3.4
Hyperbolic (5 3 3)	V6.6.10	(3.5)³	3.10.3.10	(3.5)³	3.6.5.6	(3.3)⁵	3.6.5.6	6.6.10	3.3.3.3.3.5
Hyperbolic (5 4 3)	V6.8.10	(3.5)⁴	3.10.4.10	(4.5)³	3.8.5.8	(3.4)⁵	4.6.5.6	6.8.10	3.5.3.4.3.3
Hyperbolic (5 4 4)	V8.8.10	(4.5)⁴	4.10.4.10	(4.5)⁴	4.8.5.8	(4.4)⁵	4.8.5.8	8.8.10	3.4.3.4.3.5
Hyperbolic (6 3 3)	V6.6.12	(3.6)³	3.12.3.12	(3.6)³	3.6.6.6	(3.3)⁶	3.6.6.6	6.6.12	3.3.3.3.3.6
Hyperbolic (6 4 3)	V6.8.12	(3.6)⁴	3.12.4.12	(4.6)³	3.8.6.8	(3.4)⁶	4.6.6.6	6.8.12	3.6.3.4.3.3
Hyperbolic (6 4 4)	V8.8.12	(4.6)⁴	4.12.4.12	(4.6)⁴	4.8.6.8	(4.4)⁶	4.8.6.8	8.8.12	3.6.3.4.3.4
Hyperbolic (∞ 3 3)	V6.6.∞	(3.∞)³	3.∞.3.∞	(3.∞)³	3.6.∞.6	(3.3)^∞	3.6.∞.6	6.6.∞	3.3.3.3.3.∞
Hyperbolic (∞ 4 3)	V6.8.∞	(3.∞)⁴	3.∞.4.∞	(4.∞)³	3.8.∞.8	(3.4)^∞	4.6.∞.6	6.8.∞	3.∞.3.4.3.3
Hyperbolic (∞ 4 4)	V8.8.∞	(4.∞)⁴	4.∞.4.∞	(4.∞)⁴	4.8.∞.8	(4.4)^∞	4.8.∞.8	8.8.∞	3.∞.3.4.3.4
Hyperbolic (∞ ∞ 3)	V6.∞.∞	(3.∞)^∞	3.∞.∞.∞	(∞.∞)³	3.∞.∞.∞	(3.∞)^∞	∞.6.∞.6	6.∞.∞	3.∞.3.∞.3.3
Hyperbolic (∞ ∞ 4)	V8.∞.∞	(4.∞)^∞	4.∞.∞.∞	(∞.∞)⁴	4.∞.∞.∞	(4.∞)^∞	∞.8.∞.8	8.∞.∞	3.∞.3.∞.3.4
Hyperbolic (∞ ∞ ∞)	V∞.∞.∞	(∞.∞)^∞	∞.∞.∞.∞	(∞.∞)^∞	∞.∞.∞.∞	(∞.∞)^∞	∞.∞.∞.∞	∞.∞.∞	3.∞.3.∞.3.∞

References

Coxeter Regular Polytopes, Third edition, (1973), Dover edition, ISBN 0-486-61480-8 (Chapter V: The Kaleidoscope, Section: 5.7 Wythoff's construction)
Coxeter The Beauty of Geometry: Twelve Essays, Dover Publications, 1999, ISBN 0-486-40919-8 (Chapter 3: Wythoff's Construction for Uniform Polytopes)
Coxeter, Longuet-Higgins, Miller, Uniform polyhedra, Phil. Trans. 1954, 246 A, 401–50.
Wenninger, Magnus (1974). Polyhedron Models. Cambridge University Press. ISBN 0-521-09859-9. pp. 9–10.

External links

Weisstein, Eric W. "Wythoff symbol". MathWorld.
The Wythoff symbol
Greg Egan's applet to display uniform polyhedra using Wythoff's construction method
A Shadertoy renderization of Wythoff's construction method
KaleidoTile 3 Free educational software for Windows by Jeffrey Weeks that generated many of the images on the page.
Hatch, Don. "Hyperbolic Planar Tessellations".

This article includes a mathematics-related list of lists.