Алгоритм поиска
В этой статье есть несколько проблем. Пожалуйста, помогите улучшить его или обсудите эти проблемы на странице обсуждения . ( Узнайте, как и когда удалять эти шаблонные сообщения )
|
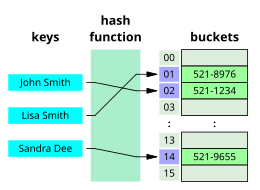
В информатике алгоритм поиска — это алгоритм, предназначенный для решения задачи поиска . Алгоритмы поиска работают для извлечения информации, хранящейся в определенной структуре данных или рассчитанной в пространстве поиска проблемной области, с дискретными или непрерывными значениями .
Хотя поисковые системы используют алгоритмы поиска, они относятся к изучению поиска информации , а не к алгоритмике.
Подходящий алгоритм поиска часто зависит от искомой структуры данных и может также включать предварительные знания о данных. Алгоритмы поиска можно сделать быстрее и эффективнее с помощью специально созданных структур базы данных, таких как деревья поиска , хэш-карты и индексы базы данных . [1] [2]
Алгоритмы поиска можно разделить в зависимости от механизма поиска на три типа алгоритмов: линейные, двоичные и хеширующие. Алгоритмы линейного поиска линейно проверяют каждую запись на наличие записи, связанной с целевым ключом. [3] Бинарный или полуинтервальный поиск неоднократно нацелен на центр структуры поиска и делит пространство поиска пополам. Алгоритмы поиска по сравнению улучшают линейный поиск за счет последовательного исключения записей на основе сравнения ключей до тех пор, пока не будет найдена целевая запись, и могут применяться к структурам данных с определенным порядком. [4] Алгоритмы цифрового поиска работают на основе свойств цифр в структурах данных с использованием числовых ключей. [5] Наконец, хеширование напрямую сопоставляет ключи с записями на основе хэш-функции . [6]
Алгоритмы часто оцениваются по их вычислительной сложности или максимальному теоретическому времени выполнения. Например, функции двоичного поиска имеют максимальную сложность O (log n ) или логарифмическое время. Проще говоря, максимальное количество операций, необходимых для поиска цели поиска, является логарифмической функцией размера пространства поиска.
Применение алгоритмов поиска
[ редактировать ]Конкретные применения алгоритмов поиска включают:
- Проблемы комбинаторной оптимизации , такие как:
- Задача выбора маршрута транспортного средства , разновидность задачи о кратчайшем пути.
- Задача о рюкзаке : учитывая набор предметов, каждый из которых имеет вес и ценность, определите количество каждого предмета, который нужно включить в коллекцию, чтобы общий вес был меньше или равен заданному пределу, а общая стоимость была такой же большой. насколько это возможно.
- Проблема с расписанием медсестры
- Проблемы удовлетворения ограничений , такие как:
- карты Проблема с раскраской
- Заполнение судоку или кроссворда
- В теории игр и особенно в комбинаторной теории игр выбор лучшего хода для следующего шага (например, с помощью алгоритма минмакс ).
- Нахождение комбинации или пароля из всего набора возможностей
- Факторизация целого числа (важная проблема в криптографии )
- Поисковая оптимизация (SEO) и оптимизация контента для веб-сканеров
- Оптимизация промышленного процесса, например химической реакции , путем изменения параметров процесса (например, температуры, давления и pH).
- Получение записи из базы данных
- Поиск максимального или минимального значения в списке или массиве
- Проверка наличия данного значения в наборе значений
Классы
[ редактировать ]Для виртуальных пространств поиска
[ редактировать ]Алгоритмы поиска виртуальных пространств используются в задаче удовлетворения ограничений , где цель состоит в том, чтобы найти набор присвоений значений определенным переменным, который будет удовлетворять конкретным математическим уравнениям и неравенствам /равенствам. Они также используются, когда цель состоит в том, чтобы найти назначение переменных, которое максимизирует или минимизирует определенную функцию этих переменных. Алгоритмы решения этих задач включают базовый поиск методом грубой силы (также называемый «наивным» или «неинформированным» поиском) и различные эвристики , которые пытаются использовать частичные знания о структуре этого пространства, такие как линейная релаксация, генерация ограничений, и распространение ограничений .
Важным подклассом являются методы локального поиска , которые рассматривают элементы пространства поиска как вершины графа с ребрами, определяемыми набором эвристик, применимых к данному случаю; и сканировать пространство, переходя от элемента к элементу по краям, например по наикрутейшему спуску или best-first критерию , или в стохастическом поиске . В эту категорию входит большое разнообразие общих метаэвристических методов, таких как имитация отжига , табу-поиск , A-команды и генетическое программирование , которые определенным образом комбинируют произвольные эвристики. Противоположностью локальному поиску будут методы глобального поиска. Этот метод применим, когда пространство поиска не ограничено и все аспекты данной сети доступны объекту, запускающему алгоритм поиска. [7]
Этот класс также включает в себя различные алгоритмы поиска по дереву , которые рассматривают элементы как вершины дерева и обходят это дерево в определенном порядке. Примеры последних включают в себя исчерпывающие методы, такие как поиск в глубину и поиск в ширину , а также различные эвристические методы обрезки дерева поиска, такие как возврат с возвратом и ветвление и граница . В отличие от общей метаэвристики, которая в лучшем случае работает только в вероятностном смысле, многие из этих методов поиска по дереву гарантированно найдут точное или оптимальное решение, если уделить достаточно времени. Это называется « полнота ».
Другой важный подкласс составляют алгоритмы исследования дерева игр с несколькими игроками, таких как шахматы или нарды , узлы которых состоят из всех возможных игровых ситуаций, которые могут возникнуть в результате текущей ситуации. Целью этих задач является нахождение хода, обеспечивающего наилучшие шансы на победу, принимая во внимание все возможные ходы противника(ов). Подобные проблемы возникают, когда людям или машинам приходится принимать последовательные решения, результаты которых не полностью находятся под их контролем, например, при роботами управлении или при планировании маркетинговой , финансовой или военной стратегии. Такого рода задачи — комбинаторный поиск — широко изучаются в контексте искусственного интеллекта . Примерами алгоритмов этого класса являются минимаксный алгоритм , альфа-бета-обрезка , а также алгоритм A* и его варианты.
Для подструктур данной структуры
[ редактировать ]Название «комбинаторный поиск» обычно используется для алгоритмов, которые ищут определенную подструктуру данной дискретной структуры , например граф, строку , конечную группу и т. д. Термин комбинаторная оптимизация обычно используется, когда цель состоит в том, чтобы найти подструктуру с максимальным (или минимальным) значением некоторого параметра. (Поскольку подструктура обычно представляется в компьютере набором целочисленных переменных с ограничениями, эти проблемы можно рассматривать как частные случаи удовлетворения ограничений или дискретной оптимизации; но они обычно формулируются и решаются в более абстрактной постановке, где внутреннее представление явно не упоминается.)
Важным и широко изученным подклассом являются графовые алгоритмы , в частности алгоритмы обхода графа , для поиска конкретных подструктур в данном графе — таких как подграфы , пути , схемы и т. д. Примеры включают алгоритм Дейкстры , алгоритм Краскала , алгоритм ближайшего соседа и алгоритм Прима .
Другим важным подклассом этой категории являются алгоритмы поиска строк , которые ищут шаблоны внутри строк. Двумя известными примерами являются алгоритмы Бойера-Мура и Кнута-Морриса-Пратта , а также несколько алгоритмов, основанных на структуре данных суффиксного дерева .
Поиск максимума функции
[ редактировать ]В 1953 году американский статистик Джек Кифер разработал поиск Фибоначчи , который можно использовать для поиска максимума унимодальной функции и который имеет множество других приложений в информатике.
Для квантовых компьютеров
[ редактировать ]Существуют также методы поиска, разработанные для квантовых компьютеров , такие как алгоритм Гровера , которые теоретически быстрее, чем линейный поиск или поиск методом грубой силы, даже без помощи структур данных или эвристики. Хотя идеи и приложения, лежащие в основе квантовых компьютеров, все еще являются полностью теоретическими, исследования проводились с использованием алгоритмов, подобных алгоритму Гровера, которые точно воспроизводят гипотетические физические версии квантовых вычислительных систем. [8]
См. также
[ редактировать ]- Обратная индукция - процесс последовательного рассуждения в обратном направлении.
- Память с адресацией по содержимому - специальный тип компьютерной памяти, используемый в некоторых аппаратных средствах приложений очень высокоскоростного поиска.
- Двухфазная эволюция - процесс, который стимулирует самоорганизацию в сложных адаптивных системах.
- Задача линейного поиска - Задача вычислительного поиска
- Никаких бесплатных обедов в поиске и оптимизации – средняя стоимость решения одинакова для любого метода.
- Рекомендательная система - система фильтрации информации для прогнозирования предпочтений пользователей, а также использование статистических методов для ранжирования результатов в очень больших наборах данных.
- Поисковая система (вычисления) - Система, помогающая искать информацию.
- Поисковая игра - игра для двух человек с нулевой суммой.
- Алгоритм выбора – метод поиска k-го наименьшего значения
- Solver - Программное обеспечение для класса математических задач.
- Алгоритм сортировки - алгоритм, который упорядочивает списки по порядку, необходимый для выполнения определенных алгоритмов поиска.
- Поисковая система в Интернете — программная система для поиска соответствующей информации на веб-
Категории:
Ссылки
[ редактировать ]Цитаты
[ редактировать ]- ^ Beame & Fich 2002 , с. 39.
- ^ Кнут 1998 , §6.5 («Поиск по вторичным ключам»).
- ^ Кнут 1998 , §6.1 («Последовательный поиск»).
- ^ Кнут 1998 , §6.2 («Поиск путем сравнения ключей»).
- ^ Кнут 1998 , §6.3 (Цифровой поиск).
- ^ Кнут 1998 , §6.4, (Хеширование).
- ^ Хантер, АХ; Пиппенджер, Николас (4 июля 2013 г.). «Локальный и глобальный поиск в графах каналов». Сети: международное путешествие . arXiv : 1004.2526 .
- ^ Лопес, Г.В.; Горин, Т; Лара, Л. (26 февраля 2008 г.). «Моделирование алгоритма квантового поиска Гровера в квантовом компьютере Изинга с ядерной спиновой цепочкой и связями первого и второго ближайших соседей». Журнал физики B: атомная, молекулярная и оптическая физика . 41 (5): 055504. arXiv : 0710.3196 . Бибкод : 2008JPhB...41e5504L . дои : 10.1088/0953-4075/41/5/055504 . S2CID 18796310 .
Библиография
[ редактировать ]Книги
[ редактировать ]- Кнут, Дональд (1998). Сортировка и поиск . Искусство компьютерного программирования . Том. 3 (2-е изд.). Ридинг, Массачусетс: Addison-Wesley Professional.
Статьи
[ редактировать ]- Бим, Пол; Фич, Вера (август 2002 г.). «Оптимальные границы проблемы предшественника и связанных с ней проблем» . Журнал компьютерных и системных наук . 65 (1): 38–72. дои : 10.1006/jcss.2002.1822 . S2CID 1991980 .
- Шмитту, Томас; Шмитту, Фейт Э. (1 августа 2002 г.). «Оптимальные границы проблемы предшественника и связанных с ней проблем» . Журнал компьютерных и системных наук . 65 (1): 38–72. дои : 10.1006/jcss.2002.1822 .