5-simplex

5-simplex Hexateron (hix)
Type	uniform 5-polytope
Schläfli symbol	{34}
Coxeter diagram
4-faces	6	6 {3,3,3}
Cells	15	15 {3,3}
Faces	20	20 {3}
Edges	15
Vertices	6
Vertex figure	5-cell
Coxeter group	A5, [34], order 720
Dual	self-dual
Base point	(0,0,0,0,0,1)
Circumradius	0.645497
Properties	convex, isogonal regular, self-dual

In five-dimensional geometry, a 5-simplex is a self-dual regular 5-polytope. It has six vertices, 15 edges, 20 triangle faces, 15 tetrahedral cells, and 6 5-cell facets. It has a dihedral angle of cos⁻¹(⁠1/5⁠), or approximately 78.46°.

The 5-simplex is a solution to the problem: Make 20 equilateral triangles using 15 matchsticks, where each side of every triangle is exactly one matchstick.

Alternate names

It can also be called a hexateron, or hexa-5-tope, as a 6-facetted polytope in 5-dimensions. The name hexateron is derived from hexa- for having six facets and teron (with ter- being a corruption of tetra-) for having four-dimensional facets.

By Jonathan Bowers, a hexateron is given the acronym hix.

As a configuration

This configuration matrix represents the 5-simplex. The rows and columns correspond to vertices, edges, faces, cells and 4-faces. The diagonal numbers say how many of each element occur in the whole 5-simplex. The nondiagonal numbers say how many of the column's element occur in or at the row's element. This self-dual simplex's matrix is identical to its 180 degree rotation.

${\begin{bmatrix}{\begin{matrix}6&5&10&10&5\\2&15&4&6&4\\3&3&20&3&3\\4&6&4&15&2\\5&10&10&5&6\end{matrix}}\end{bmatrix}}$

Regular hexateron cartesian coordinates

The hexateron can be constructed from a 5-cell by adding a 6th vertex such that it is equidistant from all the other vertices of the 5-cell.

The Cartesian coordinates for the vertices of an origin-centered regular hexateron having edge length 2 are:

${\begin{aligned}&\left({\tfrac {1}{\sqrt {15}}},\ {\tfrac {1}{\sqrt {10}}},\ {\tfrac {1}{\sqrt {6}}},\ {\tfrac {1}{\sqrt {3}}},\ \pm 1\right)\\[5pt]&\left({\tfrac {1}{\sqrt {15}}},\ {\tfrac {1}{\sqrt {10}}},\ {\tfrac {1}{\sqrt {6}}},\ -{\tfrac {2}{\sqrt {3}}},\ 0\right)\\[5pt]&\left({\tfrac {1}{\sqrt {15}}},\ {\tfrac {1}{\sqrt {10}}},\ -{\tfrac {\sqrt {3}}{\sqrt {2}}},\ 0,\ 0\right)\\[5pt]&\left({\tfrac {1}{\sqrt {15}}},\ -{\tfrac {2{\sqrt {2}}}{\sqrt {5}}},\ 0,\ 0,\ 0\right)\\[5pt]&\left(-{\tfrac {\sqrt {5}}{\sqrt {3}}},\ 0,\ 0,\ 0,\ 0\right)\end{aligned}}$

The vertices of the 5-simplex can be more simply positioned on a hyperplane in 6-space as permutations of (0,0,0,0,0,1) or (0,1,1,1,1,1). These constructions can be seen as facets of the 6-orthoplex or rectified 6-cube respectively.

Projected images

orthographic projections

Ak Coxeter plane	A5	A4
Graph
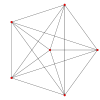
Dihedral symmetry	[6]	[5]
Ak Coxeter plane	A3	A2
Graph
Dihedral symmetry	[4]	[3]

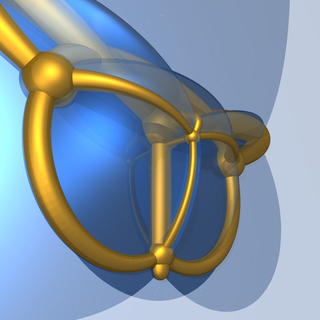Stereographic projection 4D to 3D of Schlegel diagram 5D to 4D of hexateron.

Lower symmetry forms

A lower symmetry form is a 5-cell pyramid {3,3,3}∨( ), with [3,3,3] symmetry order 120, constructed as a 5-cell base in a 4-space hyperplane, and an apex point above the hyperplane. The five sides of the pyramid are made of 5-cell cells. These are seen as vertex figures of truncated regular 6-polytopes, like a truncated 6-cube.

Another form is {3,3}∨{ }, with [3,3,2,1] symmetry order 48, the joining of an orthogonal digon and a tetrahedron, orthogonally offset, with all pairs of vertices connected between. Another form is {3}∨{3}, with [3,2,3,1] symmetry order 36, and extended symmetry [[3,2,3],1], order 72. It represents joining of 2 orthogonal triangles, orthogonally offset, with all pairs of vertices connected between.

The form { }∨{ }∨{ } has symmetry [2,2,1,1], order 8, extended by permuting 3 segments as [3[2,2],1] or [4,3,1,1], order 48.

These are seen in the vertex figures of bitruncated and tritruncated regular 6-polytopes, like a bitruncated 6-cube and a tritruncated 6-simplex. The edge labels here represent the types of face along that direction, and thus represent different edge lengths.

The vertex figure of the omnitruncated 5-simplex honeycomb, , is a 5-simplex with a petrie polygon cycle of 5 long edges. Its symmetry is isomophic to dihedral group Dih₆ or simple rotation group [6,2]⁺, order 12.

Vertex figures for uniform 6-polytopes

Join	{3,3,3}∨( )	{3,3}∨{ }	{3}∨{3}	{ }∨{ }∨{ }
Symmetry	[3,3,3,1] Order 120	[3,3,2,1] Order 48	[[3,2,3],1] Order 72	[3[2,2],1,1]=[4,3,1,1] Order 48	~[6] or ~[6,2]+ Order 12
Diagram
Polytope	truncated 6-simplex	bitruncated 6-simplex	tritruncated 6-simplex	3-3-3 prism	Omnitruncated 5-simplex honeycomb

Compound

The compound of two 5-simplexes in dual configurations can be seen in this A6 Coxeter plane projection, with a red and blue 5-simplex vertices and edges. This compound has [[3,3,3,3]] symmetry, order 1440. The intersection of these two 5-simplexes is a uniform birectified 5-simplex. = ∩ .

Related uniform 5-polytopes

It is first in a dimensional series of uniform polytopes and honeycombs, expressed by Coxeter as 1_3k series. A degenerate 4-dimensional case exists as 3-sphere tiling, a tetrahedral hosohedron.

1_3k dimensional figures

Space	Finite				Euclidean	Hyperbolic
n	4	5	6	7	8	9
Coxeter group	A3A1	A5	D6	E7	${\tilde {E}}_{7}$=E7+	${\bar {T}}_{8}$=E7++
Coxeter diagram
Symmetry	[3−1,3,1]	[30,3,1]	[31,3,1]	[32,3,1]	[[33,3,1]]	[34,3,1]
Order	48	720	23,040	2,903,040	∞
Graph					-	-
Name	13,-1	130	131	132	133	134

It is first in a dimensional series of uniform polytopes and honeycombs, expressed by Coxeter as 3_k1 series. A degenerate 4-dimensional case exists as 3-sphere tiling, a tetrahedral dihedron.

3_k1 dimensional figures

Space	Finite				Euclidean	Hyperbolic
n	4	5	6	7	8	9
Coxeter group	A3A1	A5	D6	E7	${\tilde {E}}_{7}$=E7+	${\bar {T}}_{8}$=E7++
Coxeter diagram
Symmetry	[3−1,3,1]	[30,3,1]	[[31,3,1]] = [4,3,3,3,3]	[32,3,1]	[33,3,1]	[34,3,1]
Order	48	720	46,080	2,903,040	∞
Graph					-	-
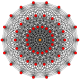
Name	31,-1	310	311	321	331	341

The 5-simplex, as 2₂₀ polytope is first in dimensional series 2_2k.

2_2k figures of n dimensions

Space	Finite			Euclidean	Hyperbolic
n	4	5	6	7	8
Coxeter group	A2A2	A5	E6	${\tilde {E}}_{6}$=E6+	E6++
Coxeter diagram
Graph				∞	∞
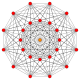
Name	22,-1	220	221	222	223

The regular 5-simplex is one of 19 uniform polytera based on the [3,3,3,3] Coxeter group, all shown here in A₅ Coxeter plane orthographic projections. (Vertices are colored by projection overlap order, red, orange, yellow, green, cyan, blue, purple having progressively more vertices)

See also

• 11-cell

References

• Gosset, T. (1900). "On the Regular and Semi-Regular Figures in Space of n Dimensions". Messenger of Mathematics. Macmillan. pp. 43–.
• Coxeter, H.S.M.:
  • — (1973). "Table I (iii): Regular Polytopes, three regular polytopes in n-dimensions (n≥5)". Regular Polytopes (3rd ed.). Dover. pp. 296. ISBN 0-486-61480-8.
  • Sherk, F. Arthur; McMullen, Peter; Thompson, Anthony C.; Weiss, Asia Ivic, eds. (1995). Kaleidoscopes: Selected Writings of H.S.M. Coxeter. Wiley. ISBN 978-0-471-01003-6.
    • (Paper 22) — (1940). "Regular and Semi Regular Polytopes I". Math. Zeit. 46: 380–407. doi:10.1007/BF01181449. S2CID 186237114.
    • (Paper 23) — (1985). "Regular and Semi-Regular Polytopes II". Math. Zeit. 188 (4): 559–591. doi:10.1007/BF01161657. S2CID 120429557.
    • (Paper 24) — (1988). "Regular and Semi-Regular Polytopes III". Math. Zeit. 200: 3–45. doi:10.1007/BF01161745. S2CID 186237142.
• Conway, John H.; Burgiel, Heidi; Goodman-Strauss, Chaim (2008). "26. Hemicubes: 1_n1". The Symmetries of Things. p. 409. ISBN 978-1-56881-220-5.
• Johnson, Norman (1991). "Uniform Polytopes" (Manuscript). Norman Johnson.
  • Johnson, N.W. (1966). The Theory of Uniform Polytopes and Honeycombs (PhD). University of Toronto.

External links

• Olshevsky, George. "Simplex". Glossary for Hyperspace. Archived from the original on 4 February 2007.
• Polytopes of Various Dimensions, Jonathan Bowers
• Multi-dimensional Glossary