Crossed pentagonal cuploid
| Crossed pentagonal cuploid | |
|---|---|
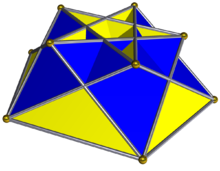 | |
| Faces | 5 triangles 5 squares 1 pentagon |
| Edges | 20 |
| Vertices | 10 |
| Vertex configuration | 5(5.4.3/2.4) 5(3.4.3/2.4/3) |
| Symmetry group | C5v, [5], (*55) |
| Rotation group | C5, [5]+, (55) |
| Dual polyhedron | crossed pentagonal keratinoid |
| Properties | non-orientable |

In geometry, the crossed pentagonal cuploid or crossed pentagonal semicupola is one member of the infinite family of cuploids. It can be obtained as a slice of the great complex rhombicosidodecahedron. As in all cupolae, the base polygon has twice as many edges and vertices as the top; but in this case the base polygon is a degenerate {10/4} decagram, as the top is a {5/4} pentagon. Hence, the degenerate base is withdrawn and the triangles are connected to the squares instead.
It may be seen as a cupola with a retrograde pentagonal base, so that the squares and triangles connect across the bases in the opposite way to the pentagonal cupola, hence intersecting each other.
Related polyhedra
[edit]| 3 | 5 | 7 | n⁄d |
|---|---|---|---|
 {3/2} Crossed triangular cuploid (upside down) |
 {5/2} Pentagrammic cuploid |
 {7/2} Heptagrammic cuploid |
2 |
| — |  {5/4} Crossed pentagonal cuploid (upside down) |
 {7/4} Crossed heptagrammic cuploid |
4 |
The crossed pentagonal cuploid may be seen as a section of the degenerate uniform polyhedron known as the great complex rhombicosidodecahedron:
 Crossed pentagonal cuploid |
 Great complex rhombicosidodecahedron | ||
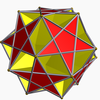
 Small ditrigonal icosidodecahedron |
 Ditrigonal dodecadodecahedron |
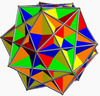
 Great ditrigonal icosidodecahedron |
 Compound of five cubes |
(In the picture of the crossed pentagonal cuploid, the pentagon is red (at the bottom and not seen), the squares yellow, and the triangles blue. In the picture of the small complex rhombicosidodecahedron, the pentagons are red, the squares blue (hidden inside and not visible), and the triangles yellow.)
Taking one pentagon from the great complex rhombicosidodecahedron, then taking the five squares that neighbour it, then taking the five triangles that border these squares results in a crossed pentagonal cuploid. As this crossed pentagonal cuploid thus shares all its edges with this polyhedron, it may be termed an edge-faceting of it. The nondegenerate uniform polyhedra sharing the same edges as the small complex rhombicosidodecahedron are the three ditrigonal polyhedra, as well as the regular compound of five cubes: hence the crossed pentagonal cuploid is also an edge-faceting of these polyhedra.
As 5/4 < 2, the crossed pentagonal cuploid does not have a membrane like the pentagrammic cuploid does.
Dual polyhedron
[edit]
The dual of the crossed pentagonal cuploid has 5 kite and 5 antiparallelogram faces, and may be called the crossed pentagonal keratinoid after Inchbald, due to it being shaped like a hollow horn:
References
[edit]- Guy Inchbald, Filling polytopes
- Richard Klitzing, Axial-Symmetrical Edge Facetings of Uniform Polyhedra
- Jim McNeill, The 5/2 semicupola and 5/4 semicupola
- Jim McNeill, Semicupolas
- Ulrich Mikloweit, Facetings of uniform polyhedra

