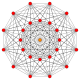
5-orthoplex

Regular 5-orthoplex (pentacross)
Orthogonal projection inside Petrie polygon
Type	Regular 5-polytope
Family	orthoplex
Schläfli symbol	{3,3,3,4} {3,3,31,1}
Coxeter-Dynkin diagrams
4-faces	32 {33}
Cells	80 {3,3}
Faces	80 {3}
Edges	40
Vertices	10
Vertex figure	16-cell
Petrie polygon	decagon
Coxeter groups	BC5, [3,3,3,4] D5, [32,1,1]
Dual	5-cube
Properties	convex, Hanner polytope

In five-dimensional geometry, a 5-orthoplex, or 5-cross polytope, is a five-dimensional polytope with 10 vertices, 40 edges, 80 triangle faces, 80 tetrahedron cells, 32 5-cell 4-faces.

It has two constructed forms, the first being regular with Schläfli symbol {3³,4}, and the second with alternately labeled (checkerboarded) facets, with Schläfli symbol {3,3,3^1,1} or Coxeter symbol 2₁₁.

It is a part of an infinite family of polytopes, called cross-polytopes or orthoplexes. The dual polytope is the 5-hypercube or 5-cube.

Alternate names

• pentacross, derived from combining the family name cross polytope with pente for five (dimensions) in Greek.
• Triacontaditeron (or triacontakaiditeron) - as a 32-facetted 5-polytope (polyteron).

As a configuration

This configuration matrix represents the 5-orthoplex. The rows and columns correspond to vertices, edges, faces, cells and 4-faces. The diagonal numbers say how many of each element occur in the whole 5-orthoplex. The nondiagonal numbers say how many of the column's element occur in or at the row's element.

${\begin{bmatrix}{\begin{matrix}10&8&24&32&16\\2&40&6&12&8\\3&3&80&4&4\\4&6&4&80&2\\5&10&10&5&32\end{matrix}}\end{bmatrix}}$

Cartesian coordinates

Cartesian coordinates for the vertices of a 5-orthoplex, centered at the origin are

(±1,0,0,0,0), (0,±1,0,0,0), (0,0,±1,0,0), (0,0,0,±1,0), (0,0,0,0,±1)

Construction

There are three Coxeter groups associated with the 5-orthoplex, one regular, dual of the penteract with the C₅ or [4,3,3,3] Coxeter group, and a lower symmetry with two copies of 5-cell facets, alternating, with the D₅ or [3^2,1,1] Coxeter group, and the final one as a dual 5-orthotope, called a 5-fusil which can have a variety of subsymmetries.

Name	Coxeter diagram	Schläfli symbol	Symmetry	Order	Vertex figure(s)
regular 5-orthoplex		{3,3,3,4}	[3,3,3,4]	3840
Quasiregular 5-orthoplex		{3,3,31,1}	[3,3,31,1]	1920
5-fusil
		{3,3,3,4}	[4,3,3,3]	3840
		{3,3,4}+{}	[4,3,3,2]	768
		{3,4}+{4}	[4,3,2,4]	384
		{3,4}+2{}	[4,3,2,2]	192
		2{4}+{}	[4,2,4,2]	128
		{4}+3{}	[4,2,2,2]	64
		5{}	[2,2,2,2]	32

Other images

orthographic projections

Coxeter plane	B5	B4 / D5	B3 / D4 / A2
Graph
Dihedral symmetry	[10]	[8]	[6]
Coxeter plane	B2	A3
Graph
Dihedral symmetry	[4]	[4]

The perspective projection (3D to 2D) of a stereographic projection (4D to 3D) of the Schlegel diagram (5D to 4D) of the 5-orthoplex. 10 sets of 4 edges form 10 circles in the 4D Schlegel diagram: two of these circles are straight lines in the stereographic projection because they contain the center of projection.

Related polytopes and honeycombs

show2k1 figures in n dimensions
Space	Finite						Euclidean	Hyperbolic
n	3	4	5	6	7	8	9	10
Coxeter group	E3=A2A1	E4=A4	E5=D5	E6	E7	E8	E9 = ${\tilde {E}}_{8}$ = E8+	E10 = ${\bar {T}}_{8}$ = E8++
Coxeter diagram
Symmetry	[3−1,2,1]	[30,2,1]	[[31,2,1]]	[32,2,1]	[33,2,1]	[34,2,1]	[35,2,1]	[36,2,1]
Order	12	120	384	51,840	2,903,040	696,729,600	∞
Graph							-	-
Name	2−1,1	201	211	221	231	241	251	261

This polytope is one of 31 uniform 5-polytopes generated from the B₅ Coxeter plane, including the regular 5-cube and 5-orthoplex.

showB5 polytopes
β5	t1β5	t2γ5	t1γ5	γ5	t0,1β5	t0,2β5	t1,2β5
t0,3β5	t1,3γ5	t1,2γ5	t0,4γ5	t0,3γ5	t0,2γ5	t0,1γ5	t0,1,2β5
t0,1,3β5	t0,2,3β5	t1,2,3γ5	t0,1,4β5	t0,2,4γ5	t0,2,3γ5	t0,1,4γ5	t0,1,3γ5
t0,1,2γ5	t0,1,2,3β5	t0,1,2,4β5	t0,1,3,4γ5	t0,1,2,4γ5	t0,1,2,3γ5	t0,1,2,3,4γ5

References

• H.S.M. Coxeter:
  • H.S.M. Coxeter, Regular Polytopes, 3rd Edition, Dover New York, 1973
  • Kaleidoscopes: Selected Writings of H.S.M. Coxeter, edited by F. Arthur Sherk, Peter McMullen, Anthony C. Thompson, Asia Ivic Weiss, Wiley-Interscience Publication, 1995, ISBN 978-0-471-01003-6 [1]
    • (Paper 22) H.S.M. Coxeter, Regular and Semi Regular Polytopes I, [Math. Zeit. 46 (1940) 380-407, MR 2,10]
    • (Paper 23) H.S.M. Coxeter, Regular and Semi-Regular Polytopes II, [Math. Zeit. 188 (1985) 559-591]
    • (Paper 24) H.S.M. Coxeter, Regular and Semi-Regular Polytopes III, [Math. Zeit. 200 (1988) 3-45]
• Norman Johnson Uniform Polytopes, Manuscript (1991)
  • N.W. Johnson: The Theory of Uniform Polytopes and Honeycombs, Ph.D. (1966)
• Klitzing, Richard. "5D uniform polytopes (polytera) x3o3o3o4o - tac".

External links

• Olshevsky, George. "Cross polytope". Glossary for Hyperspace. Archived from the original on 4 February 2007.
• Polytopes of Various Dimensions
• Multi-dimensional Glossary