Gegenbauer polynomials

In mathematics, Gegenbauer polynomials or ultraspherical polynomials C^(α)
_n(x) are orthogonal polynomials on the interval [−1,1] with respect to the weight function (1 − x²)^α–1/2. They generalize Legendre polynomials and Chebyshev polynomials, and are special cases of Jacobi polynomials. They are named after Leopold Gegenbauer.

Characterizations

• 
  Plot of the Gegenbauer polynomial C n^(m)(x) with n=10 and m=1 in the complex plane from -2-2i to 2+2i with colors created with Mathematica 13.1 function ComplexPlot3D
• 
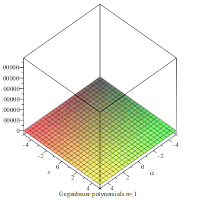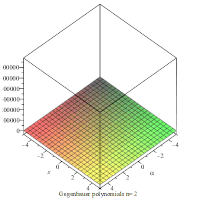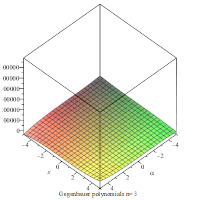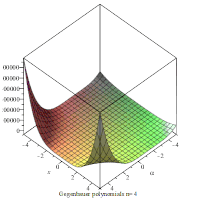
  Gegenbauer polynomials with α=1
• 
  Gegenbauer polynomials with α=2
• 
  Gegenbauer polynomials with α=3
• 
  An animation showing the polynomials on the xα-plane for the first 4 values of n.

A variety of characterizations of the Gegenbauer polynomials are available.

• The polynomials can be defined in terms of their generating function (Stein & Weiss 1971, §IV.2):

${\frac {1}{(1-2xt+t^{2})^{\alpha }}}=\sum _{n=0}^{\infty }C_{n}^{(\alpha )}(x)t^{n}\qquad (0\leq |x|<1,|t|\leq 1,\alpha >0)$

• The polynomials satisfy the recurrence relation (Suetin 2001):

${\begin{aligned}C_{0}^{(\alpha )}(x)&=1\\C_{1}^{(\alpha )}(x)&=2\alpha x\\(n+1)C_{n+1}^{(\alpha )}(x)&=2(n+\alpha )xC_{n}^{(\alpha )}(x)-(n+2\alpha -1)C_{n-1}^{(\alpha )}(x).\end{aligned}}$

• Gegenbauer polynomials are particular solutions of the Gegenbauer differential equation (Suetin 2001):

$(1-x^{2})y''-(2\alpha +1)xy'+n(n+2\alpha )y=0.\,$

When α = 1/2, the equation reduces to the Legendre equation, and the Gegenbauer polynomials reduce to the Legendre polynomials.

When α = 1, the equation reduces to the Chebyshev differential equation, and the Gegenbauer polynomials reduce to the Chebyshev polynomials of the second kind.

• They are given as Gaussian hypergeometric series in certain cases where the series is in fact finite:

$C_{n}^{(\alpha )}(z)={\frac {(2\alpha )_{n}}{n!}}\,_{2}F_{1}\left(-n,2\alpha +n;\alpha +{\frac {1}{2}};{\frac {1-z}{2}}\right).$

(Abramowitz & Stegun p. 561). Here (2α)_n is the rising factorial. Explicitly,

$C_{n}^{(\alpha )}(z)=\sum _{k=0}^{\lfloor n/2\rfloor }(-1)^{k}{\frac {\Gamma (n-k+\alpha )}{\Gamma (\alpha )k!(n-2k)!}}(2z)^{n-2k}.$

From this it is also easy to obtain the value at unit argument:

$C_{n}^{(\alpha )}(1)={\frac {\Gamma (2\alpha +n)}{\Gamma (2\alpha )n!}}.$

• They are special cases of the Jacobi polynomials (Suetin 2001):

$C_{n}^{(\alpha )}(x)={\frac {(2\alpha )_{n}}{(\alpha +{\frac {1}{2}})_{n}}}P_{n}^{(\alpha -1/2,\alpha -1/2)}(x).$

in which $(\theta )_{n}$ represents the rising factorial of $\theta$.

One therefore also has the Rodrigues formula

$C_{n}^{(\alpha )}(x)={\frac {(-1)^{n}}{2^{n}n!}}{\frac {\Gamma (\alpha +{\frac {1}{2}})\Gamma (n+2\alpha )}{\Gamma (2\alpha )\Gamma (\alpha +n+{\frac {1}{2}})}}(1-x^{2})^{-\alpha +1/2}{\frac {d^{n}}{dx^{n}}}\left[(1-x^{2})^{n+\alpha -1/2}\right].$

Orthogonality and normalization

For a fixed α > -1/2, the polynomials are orthogonal on [−1, 1] with respect to the weighting function (Abramowitz & Stegun p. 774)

$w(z)=\left(1-z^{2}\right)^{\alpha -{\frac {1}{2}}}.$

To wit, for n ≠ m,

$\int _{-1}^{1}C_{n}^{(\alpha )}(x)C_{m}^{(\alpha )}(x)(1-x^{2})^{\alpha -{\frac {1}{2}}}\,dx=0.$

They are normalized by

$\int _{-1}^{1}\left[C_{n}^{(\alpha )}(x)\right]^{2}(1-x^{2})^{\alpha -{\frac {1}{2}}}\,dx={\frac {\pi 2^{1-2\alpha }\Gamma (n+2\alpha )}{n!(n+\alpha )[\Gamma (\alpha )]^{2}}}.$

Applications

The Gegenbauer polynomials appear naturally as extensions of Legendre polynomials in the context of potential theory and harmonic analysis. The Newtonian potential in Rⁿ has the expansion, valid with α = (n − 2)/2,

${\frac {1}{|\mathbf {x} -\mathbf {y} |^{n-2}}}=\sum _{k=0}^{\infty }{\frac {|\mathbf {x} |^{k}}{|\mathbf {y} |^{k+n-2}}}C_{k}^{(\alpha )}({\frac {\mathbf {x} \cdot \mathbf {y} }{|\mathbf {x} ||\mathbf {y} |}}).$

When n = 3, this gives the Legendre polynomial expansion of the gravitational potential. Similar expressions are available for the expansion of the Poisson kernel in a ball (Stein & Weiss 1971).

It follows that the quantities $C_{k}^{((n-2)/2)}(\mathbf {x} \cdot \mathbf {y} )$ are spherical harmonics, when regarded as a function of x only. They are, in fact, exactly the zonal spherical harmonics, up to a normalizing constant.

Gegenbauer polynomials also appear in the theory of Positive-definite functions.

The Askey–Gasper inequality reads

$\sum _{j=0}^{n}{\frac {C_{j}^{\alpha }(x)}{2\alpha +j-1 \choose j}}\geq 0\qquad (x\geq -1,\,\alpha \geq 1/4).$

In spectral methods for solving differential equations, if a function is expanded in the basis of Chebyshev polynomials and its derivative is represented in a Gegenbauer/ultraspherical basis, then the derivative operator becomes a diagonal matrix, leading to fast banded matrix methods for large problems.

See also

• Rogers polynomials, the q-analogue of Gegenbauer polynomials
• Chebyshev polynomials
• Romanovski polynomials

References

• Abramowitz, Milton; Stegun, Irene Ann, eds. (1983) [June 1964]. "Chapter 22". Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables. Applied Mathematics Series. Vol. 55 (Ninth reprint with additional corrections of tenth original printing with corrections (December 1972); first ed.). Washington D.C.; New York: United States Department of Commerce, National Bureau of Standards; Dover Publications. p. 773. ISBN 978-0-486-61272-0. LCCN 64-60036. MR 0167642. LCCN 65-12253.*Koornwinder, Tom H.; Wong, Roderick S. C.; Koekoek, Roelof; Swarttouw, René F. (2010), "Orthogonal Polynomials", in Olver, Frank W. J.; Lozier, Daniel M.; Boisvert, Ronald F.; Clark, Charles W. (eds.), NIST Handbook of Mathematical Functions, Cambridge University Press, ISBN 978-0-521-19225-5, MR 2723248.
• Stein, Elias; Weiss, Guido (1971), Introduction to Fourier Analysis on Euclidean Spaces, Princeton, N.J.: Princeton University Press, ISBN 978-0-691-08078-9.
• Suetin, P.K. (2001) [1994], "Ultraspherical polynomials", Encyclopedia of Mathematics, EMS Press.

Specific