Finite potential well

The finite potential well (also known as the finite square well) is a concept from quantum mechanics. It is an extension of the infinite potential well, in which a particle is confined to a "box", but one which has finite potential "walls". Unlike the infinite potential well, there is a probability associated with the particle being found outside the box. The quantum mechanical interpretation is unlike the classical interpretation, where if the total energy of the particle is less than the potential energy barrier of the walls it cannot be found outside the box. In the quantum interpretation, there is a non-zero probability of the particle being outside the box even when the energy of the particle is less than the potential energy barrier of the walls (cf quantum tunnelling).

Particle in a 1-dimensional potential well

For the 1-dimensional case on the x-axis, the time-independent Schrödinger equation can be written as:

$$-{\frac {\hbar ^{2}}{2m}}{\frac {d^{2}\psi }{dx^{2}}}+V(x)\psi =E\psi$$ (1)

where

• $\hbar ={\frac {h}{2\pi }}$ is the reduced Planck constant,
• $h$ is the Planck constant,
• $m$ is the mass of the particle,
• $\psi$ is the (complex valued) wavefunction that we want to find,
• $V(x)$ is a function describing the potential energy at each point x, and
• $E$ is the energy, a real number, sometimes called eigenenergy.

For the case of the particle in a 1-dimensional box of length L, the potential is $V_{0}$ outside the box, and zero for x between $-L/2$ and $L/2$. The wavefunction is considered to be made up of different wavefunctions at different ranges of x, depending on whether x is inside or outside of the box. Therefore, the wavefunction is defined such that: $$\psi ={\begin{cases}\psi _{1},&{\text{if }}x<-L/2{\text{ (the region outside the well)}}\\\psi _{2},&{\text{if }}-L/2<x<L/2{\text{ (the region inside the well)}}\\\psi _{3},&{\text{if }}x>L/2{\text{ (the region outside the well)}}\end{cases}}$$

Inside the box

For the region inside the box, V(x) = 0 and Equation 1 reduces to $$-{\frac {\hbar ^{2}}{2m}}{\frac {d^{2}\psi _{2}}{dx^{2}}}=E\psi _{2}.$$ Letting $$k={\frac {\sqrt {2mE}}{\hbar }},$$ the equation becomes $${\frac {d^{2}\psi _{2}}{dx^{2}}}=-k^{2}\psi _{2}.$$

This is a well-studied differential equation and eigenvalue problem with a general solution of $$\psi _{2}=A\sin(kx)+B\cos(kx)\,.$$ Hence, $$E={\frac {k^{2}\hbar ^{2}}{2m}}.$$

Here, A and B can be any complex numbers, and k can be any real number.

Outside the box

For the region outside of the box, since the potential is constant, $V(x)=V_{0}$ and equation 1 becomes: $$-{\frac {\hbar ^{2}}{2m}}{\frac {d^{2}\psi _{1}}{dx^{2}}}=(E-V_{0})\psi _{1}$$

There are two possible families of solutions, depending on whether E is less than $V_{0}$ (the particle is bound in the potential) or E is greater than $V_{0}$ (the particle is free).

For a free particle, $E>V_{0}$, and letting $$k'={\frac {\sqrt {2m(E-V_{0})}}{\hbar }}$$ produces $${\frac {d^{2}\psi _{1}}{dx^{2}}}=-k'^{2}\psi _{1}$$ with the same solution form as the inside-well case: $$\psi _{1}=C\sin(k'x)+D\cos(k'x)$$

This analysis will focus on the bound state, where $E<V_{0}$. Letting $$\alpha ={\frac {\sqrt {2m(V_{0}-E)}}{\hbar }}$$ produces $${\frac {d^{2}\psi _{1}}{dx^{2}}}=\alpha ^{2}\psi _{1}$$ where the general solution is exponential: $$\psi _{1}=Fe^{-\alpha x}+Ge^{\alpha x}$$

Similarly, for the other region outside the box: $$\psi _{3}=He^{-\alpha x}+Ie^{\alpha x}$$

Now in order to find the specific solution for the problem at hand, we must specify the appropriate boundary conditions and find the values for A, B, F, G, H and I that satisfy those conditions.

Finding wavefunctions for the bound state

Solutions to the Schrödinger equation must be continuous, and continuously differentiable. These requirements are boundary conditions on the differential equations previously derived, that is, the matching conditions between the solutions inside and outside the well.

In this case, the finite potential well is symmetrical, so symmetry can be exploited to reduce the necessary calculations.

Summarizing the previous sections: $$\psi ={\begin{cases}\psi _{1},&{\text{if }}x<-L/2{\text{ (the region outside the box)}}\\\psi _{2},&{\text{if }}-L/2<x<L/2{\text{ (the region inside the box)}}\\\psi _{3}&{\text{if }}x>L/2{\text{ (the region outside the box)}}\end{cases}}$$ where we found $\psi _{1}$, $\psi _{2}$, and $\psi _{3}$ to be: $${\begin{aligned}\psi _{1}&=Fe^{-\alpha x}+Ge^{\alpha x}\\\psi _{2}&=A\sin(kx)+B\cos(kx)\\\psi _{3}&=He^{-\alpha x}+Ie^{\alpha x}\end{aligned}}$$

We see that as $x$ goes to $-\infty$, the $F$ term goes to infinity. Likewise, as $x$ goes to $+\infty$, the $I$ term goes to infinity. In order for the wave function to be square integrable, we must set $F=I=0$, and we have: $$\psi _{1}=Ge^{\alpha x}$$ and $$\psi _{3}=He^{-\alpha x}$$

Next, we know that the overall $\psi$ function must be continuous and differentiable. In other words, the values of the functions and their derivatives must match up at the dividing points:

$\psi _{1}(-L/2)=\psi _{2}(-L/2)$		$\psi _{2}(L/2)=\psi _{3}(L/2)$
$\left.{\frac {d\psi _{1}}{dx}}\right|_{x=-L/2}=\left.{\frac {d\psi _{2}}{dx}}\right|_{x=-L/2}$		$\left.{\frac {d\psi _{2}}{dx}}\right|_{x=L/2}=\left.{\frac {d\psi _{3}}{dx}}\right|_{x=L/2}$

These equations have two sorts of solutions, symmetric, for which $A=0$ and $G=H$, and antisymmetric, for which $B=0$ and $G=-H$. For the symmetric case we get $$He^{-\alpha L/2}=B\cos(kL/2)$$ $$-\alpha He^{-\alpha L/2}=-kB\sin(kL/2)$$ so taking the ratio gives

Roots of the equation for the quantized energy levels

$$\alpha =k\tan(kL/2).$$ Similarly for the antisymmetric case we get $$\alpha =-k\cot(kL/2).$$

Recall that both $\alpha$ and $k$ depend on the energy. What we have found is that the continuity conditions cannot be satisfied for an arbitrary value of the energy; because that is a result of the infinite potential well case. Thus, only certain energy values, which are solutions to one or either of these two equations, are allowed. Hence we find that the energy levels of the system below $V_{0}$ are discrete; the corresponding eigenfunctions are bound states. (By contrast, for the energy levels above $V_{0}$ are continuous.)

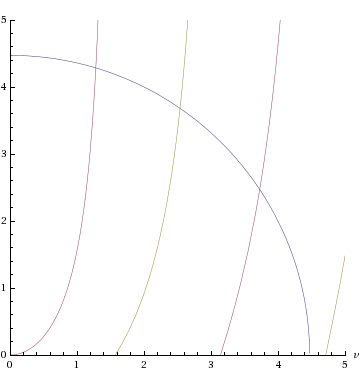
The energy equations cannot be solved analytically. Nevertheless, we will see that in the symmetric case, there always exists at least one bound state, even if the well is very shallow. Graphical or numerical solutions to the energy equations are aided by rewriting them a little. If we introduce the dimensionless variables $u=\alpha L/2$ and $v=kL/2$, and note from the definitions of $\alpha$ and $k$ that $u^{2}=u_{0}^{2}-v^{2}$, where $u_{0}^{2}=mL^{2}V_{0}/2\hbar ^{2}$, the master equations read $${\sqrt {u_{0}^{2}-v^{2}}}={\begin{cases}v\tan v,&{\text{(symmetric case) }}\\-v\cot v,&{\text{(antisymmetric case) }}\end{cases}}$$

In the plot to the right, for $u_{0}^{2}=20$, solutions exist where the blue semicircle intersects the purple or grey curves ($v\tan v$ and $-v\cot v$). Each purple or grey curve represents a possible solution, $v_{i}$ within the range ${\textstyle {\frac {\pi }{2}}(i-1)\leq v_{i}<{\frac {\pi }{2}}i}$. The total number of solutions, $N$, (i.e., the number of purple/grey curves that are intersected by the blue circle) is therefore determined by dividing the radius of the blue circle, $u_{0}$, by the range of each solution $\pi /2$ and using the floor or ceiling functions: $$N=\left\lfloor {\frac {2u_{0}}{\pi }}\right\rfloor +1=\left\lceil {\frac {2u_{0}}{\pi }}\right\rceil$$

In this case there are exactly three solutions, since $N=\lfloor 2{\sqrt {20}}/\pi \rfloor +1=\lfloor 2.85\rfloor +1=2+1=3$.

Solutions of the finite square well

$v_{1}=1.28,v_{2}=2.54$ and $v_{3}=3.73$, with the corresponding energies $$E_{n}={2\hbar ^{2}v_{n}^{2} \over mL^{2}}.$$ If we want, we can go back and find the values of the constants $A,B,G,H$ in the equations now (we also need to impose the normalisation condition). On the right we show the energy levels and wave functions in this case (where ${\textstyle x_{0}\equiv \hbar /{\sqrt {2mV_{0}}}}$).

We note that however small $u_{0}$ is (however shallow or narrow the well), there is always at least one bound state.

Two special cases are worth noting. As the height of the potential becomes large, $V_{0}\to \infty$, the radius of the semicircle gets larger and the roots get closer and closer to the values $v_{n}=n\pi /2$, and we recover the case of the infinite square well.

The other case is that of a very narrow, deep well - specifically the case $V_{0}\to \infty$ and $L\to 0$ with $V_{0}L$ fixed. As $u_{0}\propto {\sqrt {V_{0}}}L$ it will tend to zero, and so there will only be one bound state. The approximate solution is then $v^{2}=u_{0}^{2}-u_{0}^{4}$, and the energy tends to $E=-mL^{2}V_{0}^{2}/2\hbar ^{2}$. But this is just the energy of the bound state of a Delta function potential of strength $V_{0}L$, as it should be.

A simpler graphical solution for the energy levels can be obtained by normalizing the potential and the energy through multiplication by ${8m}{L^{2}}/h^{2}$. The normalized quantities are $${\tilde {V}}_{0}=V_{0}{\frac {8m}{h^{2}}}L^{2}\qquad {\tilde {E}}=E{\frac {8m}{h^{2}}}L^{2}$$ giving directly the relation between the allowed couples $(V_{0},E)$ as $${\sqrt {{\tilde {V}}_{0}}}={\sqrt {\tilde {E}}}\,\left|{\sec({\sqrt {\tilde {E}}}\,{\pi }/{2})}\right|,\qquad {\sqrt {{\tilde {V}}_{0}}}={\sqrt {\tilde {E}}}\,\left|{\csc({\sqrt {\tilde {E}}}\,{\pi }/{2})}\right|$$ for the even and odd parity wave functions, respectively. In the previous equations only the positive derivative parts of the functions have to be considered. The chart giving directly the allowed couples $(V_{0},E)$ is reported in the figure.

Unbound states

If we solve the time-independent Schrödinger equation for an energy $E>V_{0}$, the solutions will be oscillatory both inside and outside the well. Thus, the solution is never square integrable; that is, it is always a non-normalizable state. This does not mean, however, that it is impossible for a quantum particle to have energy greater than $V_{0}$, it merely means that the system has continuous spectrum above $V_{0}$. The non-normalizable eigenstates are close enough to being square integrable that they still contribute to the spectrum of the Hamiltonian as an unbounded operator.

Asymmetric well

Consider a one-dimensional asymmetric potential well given by the potential $$V(x)={\begin{cases}V_{1},&{\text{if }}-\infty <x<0{\text{ (the region outside the well)}}\\0,&{\text{if }}0<x<a{\text{ (the region inside the well)}}\\V_{2}&{\text{if }}a<x<\infty {\text{ (the region outside the well)}}\end{cases}}$$ with $V_{2}>V_{1}$. The corresponding solution for the wave function with $E<V_{1}$ is found to be $$\psi (x)={\begin{cases}c_{1}e^{k_{1}x},&{\text{for }}x<0,{\text{where }}k_{1}={\sqrt {(2m/\hbar ^{2})(V_{1}-E)}}\\c\sin(kx+\delta ),&{\text{for }}0<x<a,{\text{where }}k={\sqrt {2mE/\hbar ^{2}}}\\c_{2}e^{-k_{2}x},&{\text{for }}x>a,{\text{where }}k_{2}={\sqrt {(2m/\hbar ^{2})(V_{2}-E)}}\end{cases}}$$ and $$\sin \delta ={\frac {k\hbar }{\sqrt {2mV_{1}}}}.$$

The energy levels $E=k^{2}\hbar ^{2}/(2m)$ are determined once $k$ is solved as a root of the following transcendental equation $$ka=n\pi -\sin ^{-1}\left({\frac {k\hbar }{\sqrt {2mV_{1}}}}\right)-\sin ^{-1}\left({\frac {k\hbar }{\sqrt {2mV_{2}}}}\right)$$ where $n=1,2,3,\dots$ Existence of root to above equation is not always guaranteed, for example, one can always find a value of $a$ so small, that for given values of $V_{1}$ and $V_{2}$, there exists no discrete energy level. The results of symmetrical well is obtained from above equation by setting $V_{1}=V_{2}=V_{o}$.

Particle in a spherical potential well

Consider the following spherical potential well $$U(r)={\begin{cases}-U_{0},&{\text{if }}r<a{\text{ (the region inside the well)}}\\0,&{\text{if }}r>a{\text{ (the region outside the well)}}\end{cases}}$$ where $r$ is the radius from the origin. The solution for the wavefunction with zero angular momentum ($l=0$) and with a energy $E<0$ is given by $$\psi (r)={\begin{cases}{\frac {A}{r}}\sin kr,&{\text{for }}r<a,{\text{where }}k={\sqrt {(2m/\hbar ^{2})(U_{0}-|E|)}}\\{\frac {B}{r}}e^{-\kappa r},&{\text{for }}r>a,{\text{where }}\kappa ={\sqrt {2m|E|/\hbar ^{2}}}={\sqrt {2mU_{0}/\hbar ^{2}-k^{2}}}.\end{cases}}$$ satisfying the condition

$k\cot ka=-\kappa .$

This equation does not always have a solution indicating that in some cases, there are no bound states. The minimum depth of the potential well for which the bound state first appears at $E=0$ is given by

$U_{0,\mathrm {min} }={\frac {\pi ^{2}\hbar ^{2}}{8ma^{2}}}$

which increases with decreasing well radius $a$. Thus, bound states are not possible if the well is sufficiently shallow and narrow. For well depth slightly exceeding the minimum value, i.e., for $U_{0}/U_{0,\mathrm {min} }-1\ll 1$, the ground state energy $E_{1}$ (since we are considering $l=0$ case) is given by

$-E_{1}={\frac {\pi ^{2}}{16}}{\frac {(|U_{0}|-U_{0,\mathrm {min} })^{2}}{U_{0,\mathrm {min} }}}.$

Spherically symmetric annular well

The results above can be used to show that, as to the one-dimensional case, there is two bound states in a spherical cavity, as spherical coordinates make equivalent the radius at any direction.

The ground state (n = 1) of a spherically symmetric potential will always have zero orbital angular momentum (ℓ = n−1), and the reduced wave function $\chi (r)\equiv r\psi (r)$ satisfies the equation $$-{\frac {\hbar ^{2}}{2m}}{\frac {d^{2}\chi }{dr^{2}}}+U(r)\chi (r)=E\chi (r)$$ where $\psi (r)$ is the radial part of the wave function. Notice that for (n = 1) angular part is constant (ℓ = 0).

This is identical to the one-dimensional equation, except for the boundary conditions. As before, $$\chi (r)={\begin{cases}c_{1}\sin({k_{1}r}),&{\text{for }}r<a,{\text{ where }}k_{1}={\sqrt {2m/\hbar ^{2}(U_{1}-E)}}\\[1ex]c\sin({kr+\delta }),&{\text{for }}a<r<b,{\text{ where }}k={\sqrt {2mE/\hbar ^{2}}}\\[1ex]c_{2}e^{-k_{2}r},&{\text{for }}r>b,{\text{ where }}k_{2}={\sqrt {2m/\hbar ^{2}(U_{2}-E)}}\end{cases}}$$

The energy levels for $a<r<b$ $$E={\frac {k^{2}\hbar ^{2}}{2m}}$$ are determined once ${\displaystyle k}$ is solved as a root of the following transcendental equation $$k(b-a)=n\pi$$ where ${\displaystyle n=1,2,3,\dots }$

Existence of root to above equation is always guaranteed. The results are always with spherical symmetry. It fulfils the condition where the wave does not find any potential inside the sphere: $\chi (a)=\chi (0)=0$.

Different differential equation lay on when ℓ ≠0, so as above titles, here it is:

${\frac {d^{2}\chi }{dr^{2}}}+{\begin{Bmatrix}k^{2}-{\frac {l(l+1)}{r^{2}}}\end{Bmatrix}}\chi (r)=0$

The solution can be rationalized by some changes of variable and function to rise a Bessel like differential equation, which solution is:

${\frac {\chi (r)}{r}}={\begin{cases}Aj_{l}({k_{1}r}),&{\text{for }}r<a,{\text{ where }}k_{1}={\sqrt {2m/\hbar ^{2}(U_{1}-E)}}\\[1ex]Aj_{l}({kr})+By_{l}({kr}),&{\text{for }}a<r<b,{\text{ where }}k={\sqrt {2mE/\hbar ^{2}}}\\[1ex]B{\frac {e^{-k_{2}r}}{r}},&{\text{for }}r>b,{\text{ where }}k_{2}={\sqrt {2m/\hbar ^{2}(U_{2}-E)}}\end{cases}}$

where $j_{l}{(kr)}$ and $y_{l}({kr})$ are Bessel and Newman spherical functions respectively, and could be rewritten as function of standard Bessel function.

The energy levels for $a<r<b$

$$E={\frac {k^{2}\hbar ^{2}}{2m}}$$

are determined once ${\displaystyle k}$ is solved as a root of the following transcendental equation

$$k(b-a)={\frac {4n\pi }{2l+1}}$$

where ${\displaystyle n=1,2,3,\dots }$

Existence of root to above equation is always guaranteed. The results are always with spherical symmetry.

It fulfils the condition where the wave does not find any potential inside the sphere: $\chi (a)=\chi (0)=0$, but ${\displaystyle k}$ is solved as root of the following transcendental equation, where ${\displaystyle r<b}$:

$kb={\frac {2n\pi }{2l+1}}$

See also

• Potential well
• Delta function potential
• Infinite potential well
• Semicircle potential well
• Quantum tunnelling
• Rectangular potential barrier

Further reading

• Griffiths, David J. (2005). Introduction to Quantum Mechanics (2nd ed.). Prentice-Hall. ISBN 0-13-111892-7.
• Hall, Brian C. (2013), Quantum Theory for Mathematicians, Graduate Texts in Mathematics, vol. 267, Springer