Monogenic semigroup

Monogenic semigroup of order 9 and period 6. Numbers are exponents of the generator a; arrows indicate multiplication by a.

In mathematics, a monogenic semigroup is a semigroup generated by a single element. Monogenic semigroups are also called cyclic semigroups.

Structure

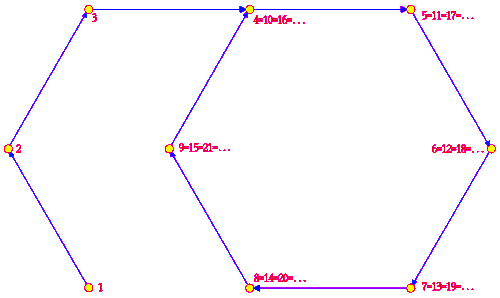
The monogenic semigroup generated by the singleton set {a} is denoted by $\langle a\rangle$. The set of elements of $\langle a\rangle$ is {a, a², a³, ...}. There are two possibilities for the monogenic semigroup $\langle a\rangle$:

• a^m = aⁿ ⇒ m = n.
• There exist m ≠ n such that a^m = aⁿ.

In the former case $\langle a\rangle$ is isomorphic to the semigroup ({1, 2, ...}, +) of natural numbers under addition. In such a case, $\langle a\rangle$ is an infinite monogenic semigroup and the element a is said to have infinite order. It is sometimes called the free monogenic semigroup because it is also a free semigroup with one generator.

In the latter case let m be the smallest positive integer such that a^m = a^x for some positive integer x ≠ m, and let r be smallest positive integer such that a^m = a^m+r. The positive integer m is referred to as the index and the positive integer r as the period of the monogenic semigroup $\langle a\rangle$. The order of a is defined as m+r−1. The period and the index satisfy the following properties:

• a^m = a^m+r
• a^m+x = a^m+y if and only if m + x ≡ m + y (mod r)
• $\langle a\rangle$ = {a, a², ... , a^m+r−1}
• K_a = {a^m, a^m+1, ... , a^m+r−1} is a cyclic subgroup and also an ideal of $\langle a\rangle$. It is called the kernel of a and it is the minimal ideal of the monogenic semigroup $\langle a\rangle$.

The pair (m, r) of positive integers determine the structure of monogenic semigroups. For every pair (m, r) of positive integers, there exists a monogenic semigroup having index m and period r. The monogenic semigroup having index m and period r is denoted by M(m, r). The monogenic semigroup M(1, r) is the cyclic group of order r.

The results in this section actually hold for any element a of an arbitrary semigroup and the monogenic subsemigroup $\langle a\rangle$ it generates.

Related notions

A related notion is that of periodic semigroup (also called torsion semigroup), in which every element has finite order (or, equivalently, in which every mongenic subsemigroup is finite). A more general class is that of quasi-periodic semigroups (aka group-bound semigroups or epigroups) in which every element of the semigroup has a power that lies in a subgroup.

An aperiodic semigroup is one in which every monogenic subsemigroup has a period of 1.

See also

• Cycle detection, the problem of finding the parameters of a finite monogenic semigroup using a bounded amount of storage space
• Special classes of semigroups