Показатель преломления

В оптике показатель преломления (или показатель преломления ) оптической среды представляет собой безразмерное число , которое указывает на свет способность этой среды преломлять .

Показатель преломления определяет, насколько путь света изгибается или преломляется при попадании в материал. Это описывается Снеллиуса законом преломления $, n 1 sin θ 1 = n 2 sin θ 2$ , где $θ 1$ и $θ 2$ — углы падения и угла преломления соответственно луча, пересекающего границу раздела двух сред с преломляющими свойствами. индексы $n 1$ и $n 2$ . Показатели преломления также определяют количество света, которое отражается при достижении границы раздела, а также критический угол полного внутреннего отражения , их интенсивность ( уравнения Френеля ) и угол Брюстера . ^[1]

Показатель преломления, $n$ , можно рассматривать как коэффициент, на который скорость и длина волны излучения уменьшаются по сравнению с их значениями в вакууме: скорость света в среде равна $v = c/ n$ , и аналогично длина волны в этой среде равна $λ = λ 0 / n$ , где $λ 0$ — длина волны этого света в вакууме. Это означает, что вакуум имеет показатель преломления, равный 1, и предполагает, что на частоту ( $f = v / λ$ ) волны показатель преломления не влияет.

Показатель преломления может меняться в зависимости от длины волны. Это приводит к тому, что белый свет при преломлении разделяется на составляющие цвета. Это называется дисперсией . Этот эффект можно наблюдать в призмах и радугах , а также в виде хроматической аберрации в линзах. Распространение света в поглощающих материалах можно описать с помощью комплексного показателя преломления. ^[2] Мнимая часть отвечает за часть затем отвечает за затухание , а действительная преломление. Для большинства материалов показатель преломления изменяется в зависимости от длины волны на несколько процентов во всем видимом спектре. Следовательно, показатели преломления материалов, о которых сообщается с использованием одного значения $n,$ должны указывать длину волны, используемую при измерении.

Концепция показателя преломления применима ко всему электромагнитному спектру , от рентгеновских лучей до радиоволн . Его также можно применить к волновым явлениям, таким как звук . В этом случае вместо скорости света используется скорость звука, и необходимо выбрать среду сравнения, отличную от вакуума. ^[3]

Что касается линз (например, очков ), линза, изготовленная из материала с высоким показателем преломления, будет тоньше и, следовательно, легче, чем обычная линза с более низким показателем преломления. Такие линзы обычно дороже в производстве, чем обычные.

Определение

Относительный показатель преломления оптической среды 2 по отношению к другой эталонной среде 1 ( $n 21$ ) определяется отношением скорости света в среде 1 к скорости света в среде 2. Это можно выразить следующим образом: $n_{21}={\frac {v_{1}}{v_{2}}}.$ Если эталонной средой 1 является вакуум , то показатель преломления среды 2 рассматривается относительно вакуума. Его просто обозначают как $n 2$ и называют абсолютным показателем преломления среды 2.

Абсолютный показатель преломления n оптической среды определяется как отношение скорости света в вакууме $c = 299792458 м/с$ к фазовой скорости $v$ света в среде $n={\frac {\mathrm {c} }{v}}.$ Поскольку $c$ является постоянной величиной, $n$ обратно пропорционально $v$ : $n\propto {\frac {1}{v}}.$ Фазовая скорость — это скорость, с которой движутся гребни или фаза волны , скорости , , которая может отличаться от групповой скорости с которой движется световой импульс или огибающая волны. ^[1] Исторически воздух при стандартизированном давлении и температуре в качестве эталонной среды обычно использовался .

История

Томас Янг, по-видимому, был человеком, который первым использовал и изобрел название «показатель преломления» в 1807 году. ^[4]В то же время он изменил это значение преломляющей силы на одно число вместо традиционного соотношения двух чисел. Соотношение имело тот недостаток, что имело разный внешний вид. Ньютон , назвавший это «пропорцией синусов падения и преломления», записал это как отношение двух чисел, например «529 к 396» (или «почти 4 к 3» для воды). ^[5] Хоксби , назвавший его «коэффициентом преломления», записал его как коэффициент с фиксированным числителем, например «10000 к 7451,9» (для мочи). ^[6] Хаттон записал это как соотношение с фиксированным знаменателем, например 1,3358 к 1 (вода). ^[7]

В 1807 году Янг не использовал символ показателя преломления. В последующие годы другие начали использовать другие символы: $n$ , $m$ и $µ$ . ^[8]^[9]^[10] Символ $n$ постепенно преобладал.

Типичные значения

Драгоценные камни бриллианты — Бриллианты имеют очень высокий показатель преломления – 2,417.

Показатель преломления также зависит от длины волны света, как это определяется уравнением Коши :

Наиболее общая форма уравнения Коши имеет вид $n(\lambda )=A+{\frac {B}{\lambda ^{2}}}+{\frac {C}{\lambda ^{4}}}+\cdots ,$ где $n$ — показатель преломления, $λ$ — длина волны, а $A$ , $B$ , $C$ и т. д. — коэффициенты , которые можно определить для материала путем подбора уравнения к измеренным показателям преломления на известных длинах волн. Коэффициенты обычно указываются для $λ$ как длины волны в вакууме в микрометрах .

Обычно достаточно использовать двухчленную форму уравнения: $n(\lambda )=A+{\frac {B}{\lambda ^{2}}},$ где коэффициенты $A$ и $B$ определяются специально для этой формы уравнения.

Выбраны показатели преломления при $λ$ = 589 нм .Ссылки см. в расширенном списке показателей преломления .
Материал	$н$
Вакуум	1
Газы при 0 °C и 1 атм.
Воздух	1.000 293
Гелий	1.000 036
Водород	1.000 132
Углекислый газ	1.000 45
Жидкости при 20 °C
Вода	1.333
Этанол	1.36
Оливковое масло	1.47
Твердые вещества
Лед	1.31
Плавленый кварц (кварц)	1.46 ^[11]
ПММА (акрил, оргстекло, люцит, плексиглас)	1.49
Оконное стекло	1.52 ^[12]
Поликарбонат (Лексан™)	1.58 ^[13]
Флинтовое стекло (типичное)	1.69
Сапфир	1.77 ^[14]
Кубический цирконий	2.15
Алмаз	2.417
Муассанит	2.65

Для видимого света большинство прозрачных сред имеют показатели преломления от 1 до 2. Несколько примеров приведены в соседней таблице. Эти значения измеряются на желтой дублетной D-линии , это как натрия с длиной волны 589 нанометров обычно делается. ^[15] Газы при атмосферном давлении имеют показатель преломления близкий к 1 из-за своей малой плотности. Почти все твердые тела и жидкости имеют показатель преломления выше 1,3, за аэрогеля исключением . Аэрогель представляет собой твердое вещество очень низкой плотности, которое можно производить с показателем преломления в диапазоне от 1,002 до 1,265. ^[16] Муассанит находится на другом конце диапазона с показателем преломления 2,65. Большинство пластмасс имеют показатель преломления в диапазоне от 1,3 до 1,7, но некоторые полимеры с высоким показателем преломления могут иметь значения до 1,76. ^[17]

Для инфракрасного света показатели преломления могут быть значительно выше. Германий прозрачен в диапазоне длин волн от 2 до 14 мкм и имеет показатель преломления около 4. ^[18] Недавно был обнаружен тип новых материалов, названных « топологическими изоляторами », которые имеют высокий показатель преломления до 6 в ближнем и среднем инфракрасном диапазоне частот. Более того, топологические изоляторы прозрачны, если они имеют наноразмерную толщину. Эти свойства потенциально важны для приложений в инфракрасной оптике. ^[19]

Показатель преломления ниже единицы

Согласно теории относительности , никакая информация не может распространяться быстрее скорости света в вакууме, но это не означает, что показатель преломления не может быть меньше 1. Показатель преломления измеряет фазовую скорость света, который не несет информации. . ^[20]^[а] Фазовая скорость — это скорость, с которой движутся гребни волны, и она может быть выше скорости света в вакууме и, таким образом, давать показатель преломления ниже 1. Это может происходить вблизи резонансных частот для поглощающих сред, в плазме , и для рентгена . В рентгеновском режиме показатели преломления ниже 1, но очень близки к 1 (исключения вблизи некоторых резонансных частот). ^[21]Например, вода имеет показатель преломления 0,999 999 74 = 1–2,6 . × 10 ⁻⁷ для рентгеновского излучения с энергией фотонов 30 кэВ ( длина волны 0,04 нм ). ^[21]

Примером плазмы с показателем преломления меньше единицы является ионосфера Земли . Поскольку показатель преломления ионосферы ( плазмы ) меньше единицы, электромагнитные волны, распространяющиеся через плазму, отклоняются «от нормали» (см. Геометрическая оптика ), позволяя радиоволнам преломляться обратно к Земле, что позволяет долгое время преломлять радиоволны. -дистанционная радиосвязь. См. также Распространение радиосигнала и Skywave . ^[22]

Отрицательный показатель преломления

Недавние исследования также продемонстрировали «существование» материалов с отрицательным показателем преломления, что может произойти, если диэлектрическая проницаемость и проницаемость имеют одновременные отрицательные значения. ^[23] Этого можно достичь с помощью периодически создаваемых метаматериалов . Возникающее в результате отрицательное преломление (т. е. обращение закона Снеллиуса ) дает возможность суперлинзу активно развивать и другие новые явления с помощью метаматериалов . ^[24]^[25]

Микроскопическое объяснение

В атомном масштабе фазовая скорость электромагнитной волны в материале замедляется, поскольку электрическое поле создает возмущение зарядов каждого атома (в первую очередь электронов ), пропорциональное электрической восприимчивости среды. (Аналогичным образом магнитное поле создает возмущение, пропорциональное магнитной восприимчивости .) Поскольку электромагнитные поля колеблются в волне, заряды в материале будут «раскачиваться» взад и вперед с одной и той же частотой. ^[1]^: 67 Таким образом, заряды излучают собственную электромагнитную волну той же частоты, но обычно с фазовой задержкой , поскольку заряды могут двигаться в противофазе с движущей их силой (см. Гармонический генератор с синусоидальным управлением ). Световая волна, распространяющаяся в среде, представляет собой макроскопическую суперпозицию (сумму) всех таких вкладов в материале: исходную волну плюс волны, излучаемые всеми движущимися зарядами. Эта волна обычно представляет собой волну той же частоты, но более короткую длину волны, чем исходная, что приводит к замедлению фазовой скорости волны. Большая часть излучения колеблющихся материальных зарядов модифицирует входящую волну, изменяя ее скорость. Однако некоторая чистая энергия будет излучаться в других направлениях или даже на других частотах (см. Рассеяние ).

В зависимости от относительной фазы исходной движущей волны и волн, излучаемых движением заряда, существует несколько возможностей:

Если электроны испускают световую волну, которая на 90° сдвинута по фазе со световой волной, сотрясающей их, это приведет к тому, что общая световая волна будет распространяться медленнее. Это нормальное преломление прозрачных материалов, таких как стекло или вода, и оно соответствует реальному показателю преломления, превышающему 1. ^[26]^{[ нужна страница ]}
Если электроны испускают световую волну, которая сдвинута по фазе на 270° со световой волной, сотрясающей их, это заставит волну двигаться быстрее. Это называется «аномальной рефракцией» и наблюдается вблизи линий поглощения (обычно в инфракрасных спектрах), в рентгеновских лучах в обычных материалах и в радиоволнах в ионосфере Земли . Это соответствует диэлектрической проницаемости меньше 1, что приводит к тому, что показатель преломления также меньше единицы, а фазовая скорость света превышает скорость света в вакууме $c$ (обратите внимание, что скорость сигнала все еще меньше $c$ , как обсуждалось выше). ). Если отклик достаточно сильный и противофазный, результатом будет отрицательное значение диэлектрической проницаемости и мнимого показателя преломления, как это наблюдается в металлах или плазме. ^[26]^{[ нужна страница ]}
Если электроны излучают световую волну, которая сдвинута по фазе на 180° со световой волной, которая их встряхивает, это будет разрушительно мешать исходному свету, уменьшая общую интенсивность света. Это поглощение света в непрозрачных материалах и соответствует мнимому показателю преломления.
Если электроны излучают световую волну, которая находится в фазе со световой волной, сотрясающей их, это усилит световую волну. Это редко, но происходит в лазерах из-за вынужденного излучения . Он соответствует мнимому показателю преломления со знаком, противоположным знаку поглощения.

Для большинства материалов на частотах видимого света фаза находится где-то между 90° и 180°, что соответствует сочетанию преломления и поглощения.

Дисперсия

Радуга — Свет разных цветов имеет немного разные показатели преломления в воде и поэтому проявляется в разных местах радуги .

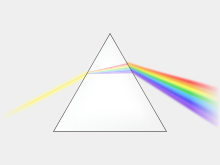
Белый луч света, проходя через треугольную призму, распадается на разные цвета. — В треугольной призме дисперсия белый заставляет разные цвета преломляться под разными углами, разделяя свет на радугу цветов. Синий цвет более отклонен (преломлен), чем красный, потому что показатель преломления синего цвета выше, чем у красного.

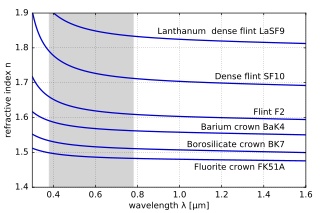
Показатель преломления материалов зависит от длины волны (и частоты ) света. ^[27] Это называется дисперсией и заставляет призмы и радуги разделять белый свет на составляющие его спектральные цвета . ^[28] Поскольку показатель преломления зависит от длины волны, будет меняться и угол преломления при переходе света от одного материала к другому. Дисперсия также приводит к тому, фокусное расстояние линз что зависит от длины волны. Это тип хроматической аберрации , которую часто необходимо корректировать в системах визуализации. В областях спектра, где материал не поглощает свет, показатель преломления имеет тенденцию уменьшаться с увеличением длины волны и, следовательно, увеличиваться с увеличением частоты. Это называется «нормальной дисперсией», в отличие от «аномальной дисперсии», при которой показатель преломления увеличивается с увеличением длины волны. ^[27] Для видимого света нормальная дисперсия означает, что показатель преломления синего света выше, чем красного.

Для оптики визуального диапазона степень дисперсии материала линзы часто измеряется числом Аббе : ^[28] $V={\frac {n_{\mathrm {yellow} }-1}{n_{\mathrm {blue} }-n_{\mathrm {red} }}}.$ Для более точного описания зависимости показателя преломления от длины волны уравнение Селлмейера . можно использовать ^[29] Это эмпирическая формула, которая хорошо подходит для описания дисперсии. коэффициенты Селлмейера Вместо показателя преломления в таблицах часто указываются .

Неоднозначность длины волны основного показателя преломления

Из-за дисперсии обычно важно указать длину волны света в вакууме, для которой измеряется показатель преломления. Обычно измерения проводятся на различных четко определенных спектральных линиях излучения .

Производители оптического стекла обычно определяют главный показатель преломления на желтой спектральной линии гелия ( 587,56 нм ) и, альтернативно, на зеленой спектральной линии ртути ( 546,07 нм ), называемых $d$ и $e$ линиями соответственно. Число Аббе определено для обоих и обозначается $V d$ и $V e$ . Спектральные данные, предоставляемые производителями стекла, также зачастую более точны для этих двух длин волн. ^[30]^[31]^[32]^[33]

Обе спектральные линии, $d$ и $e,$ являются синглетами и поэтому подходят для проведения очень точных измерений, таких как спектральный гониометрический метод. ^[34]^[35]

В практических приложениях измерения показателя преломления производятся на различных рефрактометрах, например на рефрактометре Аббе . Точность измерения таких типичных коммерческих устройств составляет порядка 0,0002. ^[36]^[37] Рефрактометры обычно измеряют показатель преломления $n D$ , определенный для дублета натрия $D$ ( 589,29 нм ), который на самом деле является средней точкой между двумя соседними желтыми спектральными линиями натрия. Желтые спектральные линии гелия ( $d$ ) и натрия ( $D$ ) находятся на расстоянии 1,73 нм друг от друга, что можно считать незначительным для типичных рефрактометров, но может вызвать путаницу и привести к ошибкам, если точность имеет решающее значение.

Все три типичных основных определения показателя преломления можно найти в зависимости от применения и региона. ^[38] поэтому во избежание двусмысленности следует использовать правильный нижний индекс.

Комплексный показатель преломления

Когда свет проходит через среду, некоторая его часть всегда поглощается . Это удобно учесть, определив комплексный показатель преломления: ${\underline {n}}=n+i\kappa .$

Здесь действительная часть $n$ является показателем преломления и указывает фазовую скорость , а мнимая часть $κ$ называется коэффициентом оптического затухания или коэффициентом поглощения , хотя $κ$ может также относиться к массовому коэффициенту затухания. ^[39]^: 3— и указывает величину затухания при распространении электромагнитной волны через материал. ^[1]^: 128

В том, что $κ$ соответствует поглощению, можно убедиться, подставив этот показатель преломления в выражение для электрического поля плоской направлении электромагнитной волны, распространяющейся в $x$ . Это можно сделать, связав комплексное волновое число $k$ с комплексным показателем преломления $n$ через $k = 2π n / λ 0$ , где $λ 0$ представляет собой длину волны в вакууме; это можно подставить в выражение плоской волны для волны, распространяющейся в направлении $x$ , как: ${\begin{aligned}\mathbf {E} (x,t)&=\operatorname {Re} \!\left[\mathbf {E} _{0}e^{i({\underline {k}}x-\omega t)}\right]\\&=\operatorname {Re} \!\left[\mathbf {E} _{0}e^{i(2\pi (n+i\kappa )x/\lambda _{0}-\omega t)}\right]\\&=e^{-2\pi \kappa x/\lambda _{0}}\operatorname {Re} \!\left[\mathbf {E} _{0}e^{i(kx-\omega t)}\right].\end{aligned}}$

Здесь мы видим, что $κ$ дает экспоненциальный спад, как и ожидалось из закона Бера – Ламберта . Поскольку интенсивность пропорциональна квадрату электрического поля, интенсивность будет зависеть от глубины проникновения в материал как

$I(x)=I_{0}e^{-4\pi \kappa x/\lambda _{0}}.$

и, таким образом, коэффициент поглощения равен $α = 4π κ / λ 0$ , ^[1]^: 128 а глубина проникновения интенсивность уменьшается в $1/ е$ раз ) равна $δp α = 1/ κ = λ0 (расстояние , /4π .$ после которого

И $n$ , и $κ$ зависят от частоты. В большинстве случаев $κ > 0$ (свет поглощается) или $κ = 0$ (свет распространяется вечно без потерь). В особых ситуациях, особенно в усиливающей среде лазеров κ , также возможно, что $< 0$ , что соответствует усилению света.

Альтернативное соглашение использует $n = n + iκ$ вместо $n = n - iκ$ , но где $κ > 0$ все еще соответствует потере. Таким образом, эти две конвенции несовместимы, и их не следует путать. Разница связана с определением синусоидальной зависимости от времени как $Re[exp(- iωt)]$ и $Re[exp(+ iωt)]$ . См. Математическое описание непрозрачности .

Диэлектрические потери и ненулевая проводимость при постоянном токе в материалах вызывают поглощение. Хорошие диэлектрические материалы, такие как стекло, имеют чрезвычайно низкую проводимость при постоянном токе, а на низких частотах диэлектрические потери также незначительны, что приводит к почти полному отсутствию поглощения. материала Однако на более высоких частотах (например, в видимом свете) диэлектрические потери могут значительно увеличить поглощение, снижая прозрачность на этих частотах.

Действительная $n$ и мнимая $κ$ части комплексного показателя преломления связаны соотношениями Крамерса – Кронига . В 1986 году А.Р. Форуи и И. Блумер вывели уравнение, описывающее $κ$ как функцию энергии фотонов $E$ , применимое к аморфным материалам. чтобы вывести соответствующее уравнение для $n$ как функции от $E.$ Затем Форуи и Блумер применили соотношение Крамерса-Кронига , Тот же формализм был применен к кристаллическим материалам Форухи и Блумером в 1988 году.

Показатель преломления и коэффициент экстинкции $n$ и $κ$ обычно измеряются на основе зависящих от них величин, таких как коэффициент отражения $R$ или коэффициент пропускания $T$ или эллипсометрические параметры $ψ$ и $δ$ . Определение $n$ и $κ$ на основе таких измеренных величин будет включать разработку теоретического выражения для $R$ или $T$ или $ψ$ и $δ$ в терминах действительной физической модели для $n$ и $κ$ . Подгоняя теоретическую модель к измеренным $R$ или $T$ или $ψ$ и $δ$ с помощью регрессионного анализа, $n$ и $κ$ можно вывести .

Рентгеновское излучение и экстремальное ультрафиолетовое излучение

Для рентгеновского излучения и крайнего ультрафиолетового излучения комплексный показатель преломления лишь незначительно отклоняется от единицы и обычно имеет действительную часть меньше 1. Поэтому его обычно записывают как $n = 1 - δ + iβ$ (или $n = 1 - δ - iβ$ с альтернативная конвенция, упомянутая выше). ^[2] Дельта частоты намного выше атомной резонансной частоты может быть определена выражением $\delta ={\frac {r_{0}\lambda ^{2}n_{\mathrm {e} }}{2\pi }}$ где $r 0$ — классический радиус электрона , $λ$ — длина волны рентгеновского излучения, а $n e$ — плотность электронов. Можно предположить, что электронная плотность — это просто количество электронов на атом $Z,$ умноженное на атомную плотность, но для более точного расчета показателя преломления необходимо заменить $Z$ на комплексный форм-фактор атома. $f=Z+f'+if''$ . Отсюда следует, что ${\begin{aligned}\delta &={\frac {r_{0}\lambda ^{2}}{2\pi }}(Z+f')n_{\text{atom}}\\\beta &={\frac {r_{0}\lambda ^{2}}{2\pi }}f''n_{\text{atom}}\end{aligned}}$ с $δ$ и $β$ обычно порядка 10 ⁻⁵ и 10 ⁻⁶.

Связь с другими величинами

Длина оптического пути

Длина оптического пути (OPL) представляет собой произведение геометрической длины $d$ пути света, проходящего через систему, и показателя преломления среды, через которую он распространяется, ^[40] ${\text{OPL}}=nd.$ Это важное понятие в оптике, поскольку оно определяет фазу света и управляет интерференцией и дифракцией света при его распространении. Согласно принципу Ферма , лучи света можно охарактеризовать как кривые, оптимизирующие длину оптического пути. ^[1]^: 68–69

Преломление

Когда свет перемещается из одной среды в другую, он меняет направление, т. е. преломляется . Если он движется из среды с показателем преломления $n 1$ в среду с показателем преломления $n 2$ , с углом падения к нормали к $поверхности θ 1$ , угол преломления $θ 2$ можно рассчитать по закону Снеллиуса : ^[41] $n_{1}\sin \theta _{1}=n_{2}\sin \theta _{2}.$

Когда свет попадает в материал с более высоким показателем преломления, угол преломления будет меньше угла падения, и свет будет преломляться по направлению к нормали к поверхности. Чем выше показатель преломления, тем ближе к нормальному направлению будет распространяться свет. При переходе в среду с более низким показателем преломления свет вместо этого будет преломляться от нормали к поверхности.

Полное внутреннее отражение

Если не существует угла $θ 2,$ удовлетворяющего закону Снеллиуса, т. е. ${\frac {n_{1}}{n_{2}}}\sin \theta _{1}>1,$ свет не может передаваться и вместо этого подвергается полному внутреннему отражению . ^[42]^: 49–50 Это происходит только при переходе к менее оптически плотному материалу, т. е. к материалу с меньшим показателем преломления. Чтобы получить полное внутреннее отражение, углы падения $θ 1$ должны быть больше критического угла. ^[43] $\theta _{\mathrm {c} }=\arcsin \!\left({\frac {n_{2}}{n_{1}}}\right)\!.$

Отражательная способность

Помимо проходящего света есть еще и отраженная часть. Угол отражения равен углу падения, а количество отраженного света определяется отражательной способностью поверхности. Коэффициент отражения можно рассчитать по показателю преломления и углу падения с помощью уравнений Френеля , который для нормального падения сводится к ^[42]^: 44

$R_{0}=\left|{\frac {n_{1}-n_{2}}{n_{1}+n_{2}}}\right|^{2}\!.$

Для обычного стекла в воздухе $n 1 = 1$ и $n 2 = 1,5$ , и, таким образом, отражается около 4% падающей мощности. ^[44] При других углах падения отражательная способность также будет зависеть от поляризации падающего света. Под определенным углом, называемым углом Брюстера , p -поляризованный свет (свет с электрическим полем в плоскости падения будет полностью проходить ). Угол Брюстера можно рассчитать по двум показателям преломления границы раздела как ^[1]^: 245 $\theta _{\mathsf {B}}=\arctan \left({\frac {n_{2}}{n_{1}}}\right)~.$

Линзы

увеличительное стекло — Сила увеличительного стекла определяется формой и показателем преломления линзы.

Фокусное расстояние линзы n определяется ее показателем преломления $и$ радиусами кривизны $R 1$ и $R 2$ ее поверхностей. Оптическая сила тонкой линзы в воздухе определяется упрощенной версией формулы Линзмейкера : ^[45] ${\frac {1}{f}}=(n-1)\left[{\frac {1}{R_{1}}}-{\frac {1}{R_{2}}}\right]\ ,$ где $f$ — фокусное расстояние линзы.

Разрешение микроскопа

Разрешение ( хорошего оптического микроскопа в основном определяется числовой апертурой ) $A Num$ его объектива . Числовая апертура, в свою очередь, определяется показателем преломления $n$ среды, заполняющей пространство между образцом и линзой, и половиной угла сбора света $θ$ по Карлссону (2007): ^[46]^: 6 $A_{\mathrm {Num} }=n\sin \theta ~.$

По этой причине масляная иммерсия обычно используется для получения высокого разрешения в микроскопии. В этом методе объектив погружают в каплю иммерсионного масла с высоким показателем преломления на исследуемом образце. ^[46]^: 14

Относительная диэлектрическая проницаемость и проницаемость

Показатель преломления электромагнитного излучения равен $n={\sqrt {\varepsilon _{\mathrm {r} }\mu _{\mathrm {r} }}},$ где $εr материала$ , — относительная диэлектрическая проницаемость а $µr —$ его относительная проницаемость . ^[47]^: 229 Показатель преломления используется в оптике в уравнениях Френеля и законе Снеллиуса ; в то время как относительная диэлектрическая проницаемость и проницаемость используются в уравнениях Максвелла и электронике. Большинство встречающихся в природе материалов немагнитны на оптических частотах, то есть $µ r$ очень близко к 1, поэтому $n$ примерно равно $\sqrt ε r$ . ^[48] В этом конкретном случае комплексная относительная диэлектрическая проницаемость $ε r$ с действительной и мнимой частями $ε r$ и $ɛ̃ r$ и комплексный показатель преломления $n$ с действительной и мнимой частями $n$ и $κ$ (последний называется «коэффициентом затухания») следуют отношение ${\underline {\varepsilon }}_{\mathrm {r} }=\varepsilon _{\mathrm {r} }+i{\tilde {\varepsilon }}_{\mathrm {r} }={\underline {n}}^{2}=(n+i\kappa )^{2},$

и их компоненты связаны соотношением: ^[49] ${\begin{aligned}\varepsilon _{\mathrm {r} }&=n^{2}-\kappa ^{2}\,,\\{\tilde {\varepsilon }}_{\mathrm {r} }&=2n\kappa \,,\end{aligned}}$

и:

${\begin{aligned}n&={\sqrt {\frac {|{\underline {\varepsilon }}_{\mathrm {r} }|+\varepsilon _{\mathrm {r} }}{2}}},\\\kappa &={\sqrt {\frac {|{\underline {\varepsilon }}_{\mathrm {r} }|-\varepsilon _{\mathrm {r} }}{2}}}.\end{aligned}}$

где $|{\underline {\varepsilon }}_{\mathrm {r} }|={\sqrt {\varepsilon _{\mathrm {r} }^{2}+{\tilde {\varepsilon }}_{\mathrm {r} }^{2}}}$ это комплексный модуль .

Волновое сопротивление

Волновое сопротивление плоской электромагнитной волны в непроводящей среде определяется выражением ${\begin{aligned}Z&={\sqrt {\frac {\mu }{\varepsilon }}}={\sqrt {\frac {\mu _{\mathrm {0} }\mu _{\mathrm {r} }}{\varepsilon _{\mathrm {0} }\varepsilon _{\mathrm {r} }}}}={\sqrt {\frac {\mu _{\mathrm {0} }}{\varepsilon _{\mathrm {0} }}}}{\sqrt {\frac {\mu _{\mathrm {r} }}{\varepsilon _{\mathrm {r} }}}}\\&=Z_{0}{\sqrt {\frac {\mu _{\mathrm {r} }}{\varepsilon _{\mathrm {r} }}}}\\&=Z_{0}{\frac {\mu _{\mathrm {r} }}{n}}\end{aligned}}$

где $Z 0$ — импеданс вакуумной волны, $ц$ и $е$ — абсолютная проницаемость и диэлектрическая проницаемость среды, $е р$ материала — относительная диэлектрическая проницаемость , а $ц р$ — его относительная проницаемость .

В немагнитных средах (т. е. в материалах с $µ r = 1$ ) $Z={Z_{0} \over n}$ и $n={Z_{0} \over Z}\,.$

Таким образом, показатель преломления в немагнитных средах представляет собой отношение волнового сопротивления вакуума к волновому сопротивлению среды.

Таким образом, отражательная способность $R 0$ между двумя средами может быть выражена как через волновые сопротивления, так и через показатели преломления как ${\begin{aligned}R_{0}&=\left|{\frac {n_{1}-n_{2}}{n_{1}+n_{2}}}\right|^{2}\\&=\left|{\frac {Z_{2}-Z_{1}}{Z_{2}+Z_{1}}}\right|^{2}\,.\end{aligned}}$

Плотность

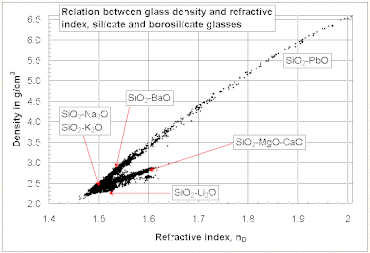
Обычно предполагается, что показатель преломления стекла увеличивается с увеличением его плотности . Однако для всех силикатных и боросиликатных стекол не существует общей линейной зависимости между показателем преломления и плотностью. Относительно высокий показатель преломления и низкую плотность можно получить с помощью стекол, содержащих оксиды легких металлов, таких как Ли ₂ О и MgO , тогда как обратная тенденция наблюдается для стекол, содержащих PbO и BaO, как показано на диаграмме справа.

Многие масла (например, оливковое масло ) и этанол являются примерами жидкостей, которые более преломляющи, но менее плотны, чем вода, вопреки общей корреляции между плотностью и показателем преломления.

Для воздуха $n - 1$ пропорционально плотности газа, пока химический состав не меняется. ^[51] Это означает, что оно также пропорционально давлению и обратно пропорционально температуре для идеальных газов . Для жидкостей можно сделать то же самое наблюдение, что и для газов: например, показатель преломления в алканах увеличивается почти идеально линейно с плотностью. С другой стороны, для карбоновых кислот плотность уменьшается с увеличением числа атомов С в гомологическом ряду. Простое объяснение этого открытия состоит в том, что значение имеет не плотность, а молярная концентрация хромофора. В гомологическом ряду это возбуждение СН-связи. Август Бир, должно быть, интуитивно понимал это, когда в 1862 году дал Гансу Х. Ландольту совет исследовать показатель преломления соединений гомологического ряда. ^[52] Хотя Ландольт не нашел этой связи, поскольку в это время теория дисперсии находилась в зачаточном состоянии, у него возникла идея молярной рефракции, которую можно приписать даже отдельным атомам. ^[53] На основе этой концепции можно рассчитать показатели преломления органических материалов.

Индекс группы

«показатель преломления групповой скорости», обычно называемый групповым показателем : Иногда определяют ^{[ нужна ссылка ]} $n_{\mathrm {g} }={\frac {\mathrm {c} }{v_{\mathrm {g} }}},$ где $vg —$ групповая скорость . Это значение не следует путать с $n$ , которое всегда определяется относительно фазовой скорости . При малой дисперсии групповую скорость можно связать с фазовой скоростью соотношением ^[42]^: 22 $v_{\mathrm {g} }=v-\lambda {\frac {\mathrm {d} v}{\mathrm {d} \lambda }},$ где $λ$ — длина волны в среде. Таким образом, в этом случае групповой индекс можно записать через зависимость показателя преломления от длины волны как $n_{\mathrm {g} }={\frac {n}{1+{\frac {\lambda }{n}}{\frac {\mathrm {d} n}{\mathrm {d} \lambda }}}}.$

Когда показатель преломления среды известен как функция длины волны в вакууме (вместо длины волны в среде), соответствующие выражения для групповой скорости и показателя будут (для всех значений дисперсии) ^[54] ${\begin{aligned}v_{\mathrm {g} }&=\mathrm {c} \!\left(n-\lambda _{0}{\frac {\mathrm {d} n}{\mathrm {d} \lambda _{0}}}\right)^{-1}\!,\\n_{\mathrm {g} }&=n-\lambda _{0}{\frac {\mathrm {d} n}{\mathrm {d} \lambda _{0}}},\end{aligned}}$ где $λ 0$ – длина волны в вакууме.

Скорость, импульс и поляризуемость

Как показано в эксперименте Физо , когда свет проходит через движущуюся среду, его скорость относительно наблюдателя, движущегося со скоростью $v$ в том же направлении, что и свет, равна: ${\begin{aligned}V&={\frac {\mathrm {c} }{n}}+{\frac {v\left(1-{\frac {1}{n^{2}}}\right)}{1+{\frac {v}{cn}}}}\\&\approx {\frac {\mathrm {c} }{n}}+v\left(1-{\frac {1}{n^{2}}}\right)\,.\end{aligned}}$

Импульс фотонов в среде с показателем преломления $n$ — сложный и противоречивый вопрос, имеющий две разные величины, имеющие разные физические интерпретации. ^[55]

Показатель преломления вещества может быть связан с его поляризуемостью уравнением Лоренца-Лоренца или с молярной преломляемостью его составляющих соотношением Гладстона-Дейла .

Преломление

В атмосферных приложениях рефракция определяется как $N = n - 1$ , часто масштабируемая как ^[56] $Н = 10 6 (н - 1)$ ^[57]^[58] или $N = 10 8 (п - 1)$ ; ^[59] коэффициенты умножения используются, поскольку показатель преломления воздуха $n$ отклоняется от единицы не более чем на несколько частей на десять тысяч.

С другой стороны, молярная рефракция мерой общей поляризуемости моля является вещества и может быть рассчитана по показателю преломления как $A={\frac {M}{\rho }}\cdot {\frac {n^{2}-1}{n^{2}+2}}\ ,$ где $ρ$ — плотность , а $M$ — молярная масса . ^[42]^: 93

Нескалярная, нелинейная или неоднородная рефракция

До сих пор мы предполагали, что преломление задается линейными уравнениями, включающими пространственно постоянный скалярный показатель преломления. Эти предположения могут быть нарушены по-разному, что будет описано в следующих подразделах.

Двойное лучепреломление

Кристалл, дающий двойное изображение текста за ним. — Кристалл кальцита , лежащий на бумаге с буквами, показывающими двойное лучепреломление.

В некоторых материалах показатель преломления зависит от поляризации и направления распространения света. ^[60] Это называется двойным лучепреломлением или оптической анизотропией .

В простейшей форме одноосного двойного лучепреломления в материале имеется только одно особое направление. Эта ось известна как оптическая ось материала. ^[1]^: 230 Свет с линейной поляризацией, перпендикулярной этой оси, будет иметь обычный показатель преломления $n o,$ тогда как свет, поляризованный параллельно, будет иметь необыкновенный показатель преломления $n e$ . ^[1]^: 236 Двойное лучепреломление материала представляет собой разницу между этими показателями преломления $Δ n = n e - n o$ . ^[1]^: 237 На свет, распространяющийся в направлении оптической оси, двойное лучепреломление не влияет, поскольку показатель преломления $не будет$ зависеть от поляризации. Для других направлений распространения свет разделится на два линейно поляризованных луча. Для света, движущегося перпендикулярно оптической оси, лучи будут иметь одинаковое направление. ^[1]^: 233 Это можно использовать для изменения направления поляризации линейно поляризованного света или для преобразования между линейной, круговой и эллиптической поляризацией с помощью волновых пластин . ^[1]^: 237

Многие кристаллы по своей природе обладают двойным лучепреломлением, но изотропные материалы, такие как пластмассы и стекло, также часто можно сделать двулучепреломляющими, вводя предпочтительное направление, например, с помощью внешней силы или электрического поля. Этот эффект называется фотоупругостью и может использоваться для выявления напряжений в конструкциях. Двулучепреломляющий материал помещается между скрещенными поляризаторами . Изменение двойного лучепреломления изменяет поляризацию и, следовательно, долю света, пропускаемую через второй поляризатор.

В более общем случае трехлучепреломляющих материалов, описываемых областью кристаллооптики , диэлектрическая проницаемость 2-го ранга представляет собой тензор (матрица 3 на 3). В этом случае распространение света нельзя описать просто показателями преломления, за исключением поляризаций вдоль главных осей.

Нелинейность

Сильное электрическое поле света высокой интенсивности (например, излучение лазера ) может привести к изменению показателя преломления среды при прохождении через нее света, что приводит к возникновению нелинейной оптики . ^[1]^: 502 Если индекс изменяется квадратично с полем (линейно с интенсивностью), это называется оптическим эффектом Керра и вызывает такие явления, как самофокусировка и автофазовая модуляция . ^[1]^: 264 Если индекс изменяется линейно с полем (нетривиальный линейный коэффициент возможен только в материалах, не обладающих инверсионной симметрией ), это известно как эффект Поккельса . ^[1]^: 265

Неоднородность

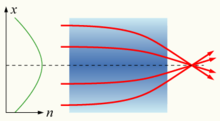
Иллюстрация с постепенно изгибающимися лучами света в толстой стеклянной плите — Линза с градиентным показателем преломления с параболическим изменением показателя преломления ( $n$ ) в зависимости от радиального расстояния ( $x$ ). Линза фокусирует свет так же, как и обычная линза.

Если показатель преломления среды не является постоянным, а постепенно меняется в зависимости от положения, материал известен как среда с градиентным показателем (GRIN) и описывается оптикой с градиентным показателем . ^[1]^: 273 Свет, проходящий через такую среду, может преломляться или фокусироваться, и этот эффект можно использовать для изготовления линз , некоторых оптических волокон и других устройств. Введение элементов GRIN в конструкцию оптической системы позволяет существенно упростить систему, сократив количество элементов почти на треть при сохранении общей производительности. ^[1]^: 276 Хрусталик человеческого глаза является примером линзы GRIN с показателем преломления, варьирующимся от примерно 1,406 во внутреннем ядре до примерно 1,386 в менее плотной коре головного мозга. ^[1]^: 203 Некоторые распространенные миражи вызваны пространственно изменяющимся показателем преломления воздуха .

Измерение показателя преломления

Однородные среды

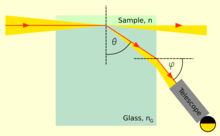
Показатель преломления жидкостей и твердых тел можно измерить с помощью рефрактометров . Обычно они измеряют некоторый угол преломления или критический угол полного внутреннего отражения. Первые лабораторные рефрактометры, продаваемые на коммерческой основе, были разработаны Эрнстом Аббе в конце 19 века. ^[61]Те же принципы используются и сегодня. В этом приборе тонкий слой измеряемой жидкости помещается между двумя призмами. Свет падает через жидкость под углами падения до 90°, т. е. лучи света параллельны поверхности. Вторая призма должна иметь показатель преломления выше, чем у жидкости, чтобы свет попадал в призму только под углами, меньшими критического угла полного отражения. Затем этот угол можно измерить, посмотрев в телескоп , ^{[ нужны разъяснения ]} или с помощью цифрового фотодетектора, помещенного в фокальную плоскость объектива. Показатель преломления $n$ жидкости затем можно рассчитать по максимальному углу пропускания $θ$ как $n = n G sin θ$ , где $n G$ - показатель преломления призмы. ^[62]

Небольшой цилиндрический рефрактометр с поверхностью для образца на одном конце и окуляром для наблюдения на другом конце. — Ручной рефрактометр, используемый для измерения содержания сахара во фруктах.

Этот тип устройств обычно используется в химических лабораториях для идентификации веществ и контроля качества . Портативные варианты используются в сельском хозяйстве , например, виноделами для определения содержания сахара в виноградном соке, а поточные технологические рефрактометры используются, например, в химической и фармацевтической промышленности для контроля процесса .

В геммологии для измерения показателей преломления и двойного лучепреломления драгоценных камней используется другой тип рефрактометра . Драгоценный камень помещен на призму с высоким показателем преломления и подсвечен снизу. Контактная жидкость с высоким показателем преломления используется для достижения оптического контакта между драгоценным камнем и призмой. При малых углах падения большая часть света будет проникать в драгоценный камень, но при больших углах в призме произойдет полное внутреннее отражение. Критический угол обычно измеряется, глядя в телескоп. ^[63]

Изменения показателя преломления

Неокрашенные биологические структуры кажутся в основном прозрачными под микроскопом светлого поля , поскольку большинство клеточных структур не ослабляют заметного количества света. Тем не менее, изменение материалов, из которых состоят эти структуры, также соответствует изменению показателя преломления. Следующие методы преобразуют такие изменения в измеримые различия амплитуд:

Для измерения пространственного изменения показателя преломления образца фазово-контрастной визуализации используются методы . Эти методы измеряют изменения фазы световой волны, выходящей из образца. Фаза пропорциональна длине оптического пути, который прошел луч света, и, таким образом, дает меру интеграла показателя преломления на пути луча. Фазу невозможно измерить непосредственно на оптических или более высоких частотах, поэтому ее необходимо преобразовать в интенсивность путем интерференции с опорным лучом. В визуальном спектре это делается с помощью фазово-контрастной микроскопии Цернике , дифференциально-интерференционно-контрастной микроскопии (ДИК) или интерферометрии .

Фазово-контрастная микроскопия Цернике вносит фазовый сдвиг в низкочастотные компоненты с изображения помощью фазосдвигающего кольца в плоскости Фурье образца, так что высокопространственно-частотные части изображения могут интерферировать с низкочастотными. опорный луч. В DIC освещение разделяется на два луча, которые имеют разную поляризацию, по-разному сдвинуты по фазе и сдвинуты в поперечном направлении на несколько разную величину. После образца две части интерферируют, давая изображение производной длины оптического пути в направлении разницы поперечного смещения. ^[46] В интерферометрии освещение разделяется на два луча частично отражающим зеркалом . Один из лучей пропускают через образец, прежде чем они объединятся, чтобы интерферировать и дать прямое изображение фазовых сдвигов. Если изменения длины оптического пути превышают длину волны, изображение будет содержать полосы.

Существует несколько методов фазово-контрастной рентгеновской визуализации для определения 2D или 3D пространственного распределения показателя преломления образцов в рентгеновском режиме. ^[64]

Приложения

Показатель преломления — важное свойство компонентов любого оптического прибора . Он определяет фокусирующую способность линз, рассеивающую способность призм, отражательную способность покрытий линз и светопроводящую природу оптического волокна . Поскольку показатель преломления является фундаментальным физическим свойством вещества, его часто используют для идентификации конкретного вещества, подтверждения его чистоты или измерения его концентрации. Показатель преломления используется для измерения твердых тел, жидкостей и газов. Чаще всего его используют для измерения концентрации растворенного вещества в водном растворе . Его также можно использовать в качестве полезного инструмента для различения различных типов драгоценных камней благодаря уникальной переливчатости каждого отдельного камня. Рефрактометр – это прибор , используемый для измерения показателя преломления. Для раствора сахара показатель преломления можно использовать для определения содержания сахара (см. Брикс ).

См. также

Сноски

^ Одним из последствий того, что действительная часть $n$ меньше единицы, является то, что это означает, что фазовая скорость внутри материала ⁠ $c$ / $n$ ⁠ , больше скорости света $c$ . Однако это не нарушает закон относительности, который требует, чтобы только сигналы, несущие информацию, не перемещались быстрее, чем $c$ . Такие сигналы движутся с групповой скоростью, а не с фазовой скоростью, и можно показать, что групповая скорость на самом деле меньше $c$ . ^[20]

Ссылки

^ Перейти обратно: ^а ^б ^с ^д ^и ^ж ^г ^час ^я ^дж ^к ^л ^м ^н ^тот ^п ^д ^р Хехт, Юджин (2002). Оптика . Аддисон-Уэсли. ISBN 978-0-321-18878-6 .
^ Перейти обратно: ^а ^б Эттвуд, Дэвид (1999). Мягкое рентгеновское излучение и сильное ультрафиолетовое излучение: принципы и применение . Издательство Кембриджского университета. п. 60. ИСБН 978-0-521-02997-1 .
^ Кинслер, Лоуренс Э. (2000). Основы акустики . Джон Уайли. п. 136 . ISBN 978-0-471-84789-2 .
^ Янг, Томас (1807). Курс лекций по натуральной философии и механическим искусствам . Дж. Джонсон. п. 413 .
^ Ньютон, Исаак (1730). Оптика: или Трактат об отражениях, преломлениях, изгибах и цветах света . Уильям Иннис в Вест-Энде собора Святого Павла. п. 247 .
^ Хоксби, Фрэнсис (1710). «Описание аппарата для проведения экспериментов по преломлению жидкостей». Философские труды Лондонского королевского общества . 27 (325–336): 207. doi : 10.1098/rstl.1710.0015 . S2CID 186208526 .
^ Хаттон, Чарльз (1795). Философско-математический словарь . п. 299. Архивировано из оригинала 22 февраля 2017 г.
^ Фраунгофера, Йозефа (1817). «Определение преломляющей и цветорассеивающей способности различных видов стекол». Меморандумы Королевской академии наук в Мюнхене [ Журнал Королевской академии наук в Мюнхене ] (на немецком языке). 5 : 208. Архивировано из оригинала 22 февраля 2017 г. Показатель коэффициента преломления – это показатель преломления.
^ Брюстер, Дэвид (1815). «О строении двоякопреломляющих кристаллов» . Философский журнал . 45 (202): 126. дои : 10.1080/14786441508638398 . Архивировано из оригинала 22 февраля 2017 г.
^ Гершель, Джон Ф.В. (1828). К теории света . п. 368. Архивировано из оригинала 24 ноября 2015 г.
^ Малитсон (1965). «База данных показателей преломления» . refractiveindex.info . Проверено 20 июня 2018 г.
^ Фаик, Калифорния; Финн, АН (июль 1931 г.). «Показатель преломления некоторых натриево-известково-кремнеземных стекол как функция состава» (PDF) . Национальный институт стандартов и технологий. Архивировано (PDF) из оригинала 30 декабря 2016 г. Проверено 11 декабря 2016 г.
^ Султанова Н.; Касарова С.; Николов И. (октябрь 2009 г.). «Дисперсионные свойства оптических полимеров» . Acta Physica Polonica А. 116 (4): 585–587. Бибкод : 2009AcPPA.116..585S . дои : 10.12693/APhysPolA.116.585 .
^ Таппинг, Дж.; Рейли, М.Л. (1 мая 1986 г.). «Показатель преломления сапфира от 24 до 1060°С для длин волн 633 и 799 нм» . Журнал Оптического общества Америки А. 3 (5): 610. Бибкод : 1986JOSAA...3..610T . дои : 10.1364/JOSAA.3.000610 .
^ «Судебно-медицинская экспертиза, определение показателя преломления стекла» . Лабораторные службы ФБР. Архивировано из оригинала 10 сентября 2014 г. Проверено 8 сентября 2014 г.
^ Табата, М.; и др. (2005). Разработка кремнеземного аэрогеля любой плотности (PDF) . Протокол конференции симпозиума по ядерной науке IEEE. Том. 2. С. 816–818. дои : 10.1109/NSSMIC.2005.1596380 . ISBN 978-0-7803-9221-2 . S2CID 18187536 . Архивировано из оригинала (PDF) 18 мая 2013 г.
^ Садайори, Наоки; Хотта, Юджи (2004). «Поликарбодиимид с высоким показателем преломления и способ его получения» . Патентное ведомство США. Патент США 2004/0158021 A1 – через Google Patents.
^ Тоси, Джеффри Л., статья об общих инфракрасных оптических материалах в Справочнике по фотонике, по состоянию на 10 сентября 2014 г.
^ Юэ, Цзэнцзи; Цай, Боюань; Ван, Лан; Ван, Сяолинь; Гу, Мин (01 марта 2016 г.). «Плазмонные диэлектрические наноструктуры ядро-оболочка со сверхвысоким показателем преломления» . Достижения науки . 2 (3): e1501536. Бибкод : 2016SciA....2E1536Y . дои : 10.1126/sciadv.1501536 . ISSN 2375-2548 . ПМЦ 4820380 . ПМИД 27051869 .
^ Перейти обратно: ^а ^б Альс-Нильсен, Дж.; МакМорроу, Д. (2011). Элементы современной рентгеновской физики . Вайли-ВЧ. п. 25 . ISBN 978-0-470-97395-0 .
^ Перейти обратно: ^а ^б Гулликсон, Эрик. «Взаимодействие рентгеновских лучей с веществом» . Оптические константы. Центр рентгеновской оптики . Лаборатория Лоуренса Беркли . Архивировано из оригинала 27 августа 2011 г. Проверено 30 августа 2011 г.
^ Ложь, Финн (1967). Высокочастотная радиосвязь с акцентом на полярные проблемы . Консультативная группа по аэрокосмическим исследованиям и разработкам. стр. 1–7.
^ Веселаго, В.Г. (1968). «Электродинамика веществ с одновременно отрицательными значениями ε и μ». Успехи советской физики . 10 (4): 509–514. Бибкод : 1968СвФУ..10..509В . дои : 10.1070/PU2003v046n07ABEH001614 . S2CID 250862458 .
^ Пендри, Дж.Б.; Шуриг, Д.; Смит, Д.Р. (8 декабря 2009 г.). «Аппарат, методы и системы электромагнитного сжатия» . Патентное ведомство США. Патент США 7629941 – через Google Patents.
^ Шалаев, В.М. (2007). «Оптические метаматериалы с отрицательным преломлением». Природная фотоника . 1 (1): 41–48. Бибкод : 2007NaPho...1...41S . дои : 10.1038/nphoton.2006.49 . S2CID 170678 .
^ Перейти обратно: ^а ^б Фейнман, Ричард П. (2011). В основном механика, радиация и тепло . Фейнмановские лекции по физике. Том. 1 (изд. «Новое тысячелетие»). Основные книги. ISBN 978-0-465-02493-3 .
^ Перейти обратно: ^а ^б Пашотта, Рюдигер. «Хроматическая дисперсия» . Энциклопедия фотоники RP . Архивировано из оригинала 29 июня 2015 г. Проверено 13 августа 2023 г.
^ Перейти обратно: ^а ^б Нейв, Карл Р. (2000). «Рассеивание» . Гиперфизика . Кафедра физики и астрономии Университета штата Джорджия. Архивировано из оригинала 24 сентября 2014 г. Проверено 13 августа 2023 г.
^ Пашотта, Рюдигер. «Формула Зельмейера» . Энциклопедия фотоники RP . Архивировано из оригинала 19 марта 2015 г. Проверено 8 сентября 2014 г.
^ Компания Шотт. «Интерактивная диаграмма Аббе» . Шотт.com . Проверено 13 августа 2023 г.
^ Корпорация Охара. «Оптические свойства» . Охаракорп.com . Проверено 15 августа 2022 г.
^ Группа Хойя. «Оптические свойства» . Оптическое подразделение Hoya Group . Проверено 13 августа 2023 г.
^ Лентес, Франк-Томас; Клемент, Марк К.Т.; Нейрот, Норберт; Хоффманн, Ханс-Юрген; Хайден, Юико Т.; Хайден, Джозеф С.; Кольберг, Уве; Вольф, Силке (1998). «Оптические свойства». У Баха, Ганс; Нейрот, Норберт (ред.). Свойства оптического стекла . Серия Шотта о стекле и стеклокерамике. п. 30. дои : 10.1007/978-3-642-57769-7 . ISBN 978-3-642-63349-2 .
^ Крей, Стефан; Прочь, Деннис; Рупрехт, Айко (08 марта 2014 г.). «Измерение показателя преломления прецизионными гониометрами: сравнительное исследование» . В Соскинде Яков Григорьевич; Олсон, Крейг (ред.). Учеб. SPIE 8992, Фотонное приборостроение . SPIE OPTO, 2014. Том. 8992. Сан-Франциско, Калифорния: SPIE. стр. 56–65. Бибкод : 2014SPIE.8992E..0DK . дои : 10.1117/12.2041760 . S2CID 120544352 .
^ Рупп, Фабиан; Джедамзик, Ральф; Бартелмесс, Лотар; Петцольд, Уве (12 сентября 2021 г.). «Современный способ измерения показателя преломления оптического стекла в компании SCHOTT» . В Фелькеле, Рейнхард; Гейл, Роланд; Отадуй, Дейце (ред.). Оптическое производство, испытания и метрология VII . Том. 11873. ШПИОН. стр. 15–22. Бибкод : 2021SPIE11873E..08R . дои : 10.1117/12.2597023 . ISBN 9781510645905 . S2CID 240561530 . {{cite book}}: |journal= игнорируется ( помогите )
^ «Рефрактометр Аббе | ATAGO CO., LTD» . www.atago.net . Проверено 15 августа 2022 г.
^ «Многоволновой рефрактометр Аббе» . Нова-Тек Интернешнл . Проверено 15 августа 2022 г.
^ Бах, Ганс; Нейрот, Норберт, ред. (1998). Свойства оптического стекла . Серия Шотта о стекле и стеклокерамике. п. 267. дои : 10.1007/978-3-642-57769-7 . ISBN 978-3-642-63349-2 .
^ Дрессельхаус, MS (1999). «Физика твердого тела, часть II. Оптические свойства твердых тел» (PDF) . Курс 6.732 Физика твердого тела . Массачусетский технологический институт. Архивировано (PDF) из оригинала 24 июля 2015 г. Проверено 5 января 2015 г.
^ Р. Пашотта, статья об оптической толщине. Архивировано 22 марта 2015 г. на Wayback Machine в Энциклопедии лазерной физики и технологий. Архивировано 13 августа 2015 г. на Wayback Machine , доступ 8 сентября 2014 г.
^ Р. Пашотта, статья о рефракции. Архивировано 28 июня 2015 г. в Wayback Machine в Энциклопедии лазерной физики и технологий. Архивировано 13 августа 2015 г. в Wayback Machine , доступ: 8 сентября 2014 г.
^ Перейти обратно: ^а ^б ^с ^д Борн, Макс ; Вольф, Эмиль (1999). Принципы оптики (7-е расширенное изд.). Архив Кубка. п. 22 . ISBN 978-0-521-78449-8 .
^ Пашотта, Р. «Полное внутреннее отражение» . Энциклопедия фотоники RP . Архивировано из оригинала 28 июня 2015 г. Проверено 16 августа 2015 г.
^ Свенсон, Джим (10 ноября 2009 г.). «Показатель преломления минералов» . Ньютон BBS / Аргоннская национальная лаборатория. Министерство энергетики США. Архивировано из оригинала 28 мая 2010 года . Проверено 28 июля 2010 г. Включает материалы, являющиеся общественным достоянием Министерства энергетики США.
^ Нейв, Карл Р. «Формула производителей линз» . Гиперфизика . Кафедра физики и астрономии. Государственный университет Джорджии. Архивировано из оригинала 26 сентября 2014 г. Проверено 8 сентября 2014 г.
^ Перейти обратно: ^а ^б ^с Карлссон, Кьелл (2007). Световая микроскопия (PDF) (Отчет). Архивировано (PDF) из оригинала 2 апреля 2015 г. Проверено 2 января 2015 г.
^ Блини, Б .; Блини, Б.И. (1976). Электричество и магнетизм (Третье изд.). Издательство Оксфордского университета . ISBN 978-0-19-851141-0 .
^ Эндрюс, Дэвид Л. (24 февраля 2015 г.). Фотоника, Том 2: Нанофотонные структуры и материалы . Джон Уайли и сыновья. п. 54. ИСБН 978-1-118-22551-6 .
^ Вутен, Фредерик (1972). Оптические свойства твердых тел . Нью-Йорк: Академическая пресса . п. 49. ИСБН 978-0-12-763450-0 . (онлайн-pdf) Архивировано 3 октября 2011 г. в Wayback Machine.
^ «Расчет показателя преломления стекол» . Статистический расчет и определение свойств стекла . Архивировано из оригинала 15 октября 2007 г.
^ Стоун, Джек А.; Циммерман, Джей Х. (28 декабря 2011 г.). «Показатель преломления воздуха» . Инструментарий инженерной метрологии . Национальный институт стандартов и технологий (NIST). Архивировано из оригинала 11 января 2014 г. Проверено 11 января 2014 г.
^ Ландольт, Х. (январь 1862 г.). «О показателях преломления жидких гомологичных соединений» . Анналы физики . 193 (11): 353–385. дои : 10.1002/andp.18621931102 . ISSN 0003-3804 .
^ Ландольт, Х. (январь 1864 г.). «О влиянии атомистического состава С, Н и Осодержащих жидких соединений на распространение света» . Анналы физики . 199 (12): 595–628. дои : 10.1002/andp.18641991206 . ISSN 0003-3804 .
^ Бор, З.; Освай, К.; Рац, Б.; Сабо, Г. (1990). «Измерение группового показателя преломления интерферометром Майкельсона». Оптические коммуникации . 78 (2): 109–112. Бибкод : 1990OptCo..78..109B . дои : 10.1016/0030-4018(90)90104-2 .
^ Милонни, Питер В.; Бойд, Роберт В. (31 декабря 2010 г.). «Импульс света в диэлектрической среде» . Достижения оптики и фотоники . 2 (4): 519. Бибкод : 2010AdOP....2..519M . дои : 10.1364/AOP.2.000519 . ISSN 1943-8206 .
^ Янг, AT (2011). «Преломление воздуха» . Архивировано из оригинала 10 января 2015 года . Проверено 31 июля 2014 г.
^ Баррелл, Х.; Сирс, Дж. Э. (1939). «Преломление и дисперсия воздуха для видимого спектра» . Философские труды Лондонского королевского общества . А. Математические и физические науки. 238 (786): 1–64. Бибкод : 1939RSPTA.238....1B . дои : 10.1098/rsta.1939.0004 . JSTOR 91351 .
^ Апарисио, Хосеп М.; Ларош, Стефан (2 июня 2011 г.). «Оценка проявления атмосферной рефракции для сигналов GPS» . Журнал геофизических исследований . 116 (Д11): Д11104. Бибкод : 2011JGRD..11611104A . дои : 10.1029/2010JD015214 .
^ Сиддор, ЧП (1996). «Показатель преломления воздуха: новые уравнения для видимого и ближнего инфракрасного диапазона». Прикладная оптика . 35 (9): 1566–1573. Бибкод : 1996ApOpt..35.1566C . дои : 10.1364/ao.35.001566 . ПМИД 21085275 .
^ Р. Пашотта, статья о двойном лучепреломлении. Архивировано 3 июля 2015 г. в Wayback Machine в Энциклопедии лазерной физики и технологий. Архивировано 13 августа 2015 г. в Wayback Machine , по состоянию на 9 сентября 2014 г.
^ «Эволюция рефрактометра Аббе» . Государственный университет Гумбольдта, Ричард А. Паселк. 1998. Архивировано из оригинала 12 июня 2011 г. Проверено 3 сентября 2011 г.
^ «Рефрактометры и рефрактометрия» . Рефрактометр.пл. 2011. Архивировано из оригинала 20 октября 2011 г. Проверено 3 сентября 2011 г.
^ «Рефрактометр» . Геммологический проект. Архивировано из оригинала 10 сентября 2011 г. Проверено 3 сентября 2011 г.
^ Фицджеральд, Ричард (июль 2000 г.). «Фазочувствительная рентгеновская визуализация» . Физика сегодня . 53 (7): 23. Бибкод : 2000ФТ....53г..23Ф . дои : 10.1063/1.1292471 . S2CID 121322301 .

Внешние ссылки

Калькулятор NIST для определения показателя преломления воздуха
Диэлектрические материалы
Мир науки
Онлайн-база данных Filmetrics Бесплатная база данных с информацией о показателях преломления и коэффициентах поглощения
RefractiveIndex.INFO База данных индекса преломления с онлайн-построением графиков и параметризацией данных
LUXPOP. Архивировано 7 сентября 2013 г. в Wayback Machine. Расчеты тонких пленок и объемного показателя преломления и фотоники.
Фейнмановские лекции по физике Vol. II гл. 32: Показатель преломления плотных материалов

[21] Одним из последствий того, что действительная часть $n$ меньше единицы, является то, что это означает, что фазовая скорость внутри материала ⁠ $c$ / $n$ ⁠ , больше скорости света $c$ . Однако это не нарушает закон относительности, который требует, чтобы только сигналы, несущие информацию, не перемещались быстрее, чем $c$ . Такие сигналы движутся с групповой скоростью, а не с фазовой скоростью, и можно показать, что групповая скорость на самом деле меньше $c$ . ^[20]

[Hecht-1] Перейти обратно: ^а ^б ^с ^д ^и ^ж ^г ^час ^я ^дж ^к ^л ^м ^н ^тот ^п ^д ^р Хехт, Юджин (2002). Оптика . Аддисон-Уэсли. ISBN 978-0-321-18878-6 .

[Attwood-2] Перейти обратно: ^а ^б Эттвуд, Дэвид (1999). Мягкое рентгеновское излучение и сильное ультрафиолетовое излучение: принципы и применение . Издательство Кембриджского университета. п. 60. ИСБН 978-0-521-02997-1 .

[Kinsler-3] Кинслер, Лоуренс Э. (2000). Основы акустики . Джон Уайли. п. 136 . ISBN 978-0-471-84789-2 .

[4] Янг, Томас (1807). Курс лекций по натуральной философии и механическим искусствам . Дж. Джонсон. п. 413 .

[Newton-5] Ньютон, Исаак (1730). Оптика: или Трактат об отражениях, преломлениях, изгибах и цветах света . Уильям Иннис в Вест-Энде собора Святого Павла. п. 247 .

[Hauksbee-6] Хоксби, Фрэнсис (1710). «Описание аппарата для проведения экспериментов по преломлению жидкостей». Философские труды Лондонского королевского общества . 27 (325–336): 207. doi : 10.1098/rstl.1710.0015 . S2CID 186208526 .

[Hutton-7] Хаттон, Чарльз (1795). Философско-математический словарь . п. 299. Архивировано из оригинала 22 февраля 2017 г.

[Fraunhofer-8] Фраунгофера, Йозефа (1817). «Определение преломляющей и цветорассеивающей способности различных видов стекол». Меморандумы Королевской академии наук в Мюнхене [ Журнал Королевской академии наук в Мюнхене ] (на немецком языке). 5 : 208. Архивировано из оригинала 22 февраля 2017 г. Показатель коэффициента преломления – это показатель преломления.

[Brewster-9] Брюстер, Дэвид (1815). «О строении двоякопреломляющих кристаллов» . Философский журнал . 45 (202): 126. дои : 10.1080/14786441508638398 . Архивировано из оригинала 22 февраля 2017 г.

[Herschel-10] Гершель, Джон Ф.В. (1828). К теории света . п. 368. Архивировано из оригинала 24 ноября 2015 г.

[11] Малитсон (1965). «База данных показателей преломления» . refractiveindex.info . Проверено 20 июня 2018 г.

[12] Фаик, Калифорния; Финн, АН (июль 1931 г.). «Показатель преломления некоторых натриево-известково-кремнеземных стекол как функция состава» (PDF) . Национальный институт стандартов и технологий. Архивировано (PDF) из оригинала 30 декабря 2016 г. Проверено 11 декабря 2016 г.

[13] Султанова Н.; Касарова С.; Николов И. (октябрь 2009 г.). «Дисперсионные свойства оптических полимеров» . Acta Physica Polonica А. 116 (4): 585–587. Бибкод : 2009AcPPA.116..585S . дои : 10.12693/APhysPolA.116.585 .

[14] Таппинг, Дж.; Рейли, М.Л. (1 мая 1986 г.). «Показатель преломления сапфира от 24 до 1060°С для длин волн 633 и 799 нм» . Журнал Оптического общества Америки А. 3 (5): 610. Бибкод : 1986JOSAA...3..610T . дои : 10.1364/JOSAA.3.000610 .

[FBI-15] «Судебно-медицинская экспертиза, определение показателя преломления стекла» . Лабораторные службы ФБР. Архивировано из оригинала 10 сентября 2014 г. Проверено 8 сентября 2014 г.

[16] Табата, М.; и др. (2005). Разработка кремнеземного аэрогеля любой плотности (PDF) . Протокол конференции симпозиума по ядерной науке IEEE. Том. 2. С. 816–818. дои : 10.1109/NSSMIC.2005.1596380 . ISBN 978-0-7803-9221-2 . S2CID 18187536 . Архивировано из оригинала (PDF) 18 мая 2013 г.

[17] Садайори, Наоки; Хотта, Юджи (2004). «Поликарбодиимид с высоким показателем преломления и способ его получения» . Патентное ведомство США. Патент США 2004/0158021 A1 – через Google Patents.

[18] Тоси, Джеффри Л., статья об общих инфракрасных оптических материалах в Справочнике по фотонике, по состоянию на 10 сентября 2014 г.

[19] Юэ, Цзэнцзи; Цай, Боюань; Ван, Лан; Ван, Сяолинь; Гу, Мин (01 марта 2016 г.). «Плазмонные диэлектрические наноструктуры ядро-оболочка со сверхвысоким показателем преломления» . Достижения науки . 2 (3): e1501536. Бибкод : 2016SciA....2E1536Y . дои : 10.1126/sciadv.1501536 . ISSN 2375-2548 . ПМЦ 4820380 . ПМИД 27051869 .

[Als-Nielsen2011-20] Перейти обратно: ^а ^б Альс-Нильсен, Дж.; МакМорроу, Д. (2011). Элементы современной рентгеновской физики . Вайли-ВЧ. п. 25 . ISBN 978-0-470-97395-0 .

[CXRO-22] Перейти обратно: ^а ^б Гулликсон, Эрик. «Взаимодействие рентгеновских лучей с веществом» . Оптические константы. Центр рентгеновской оптики . Лаборатория Лоуренса Беркли . Архивировано из оригинала 27 августа 2011 г. Проверено 30 августа 2011 г.

[23] Ложь, Финн (1967). Высокочастотная радиосвязь с акцентом на полярные проблемы . Консультативная группа по аэрокосмическим исследованиям и разработкам. стр. 1–7.

[veselago1968-24] Веселаго, В.Г. (1968). «Электродинамика веществ с одновременно отрицательными значениями ε и μ». Успехи советской физики . 10 (4): 509–514. Бибкод : 1968СвФУ..10..509В . дои : 10.1070/PU2003v046n07ABEH001614 . S2CID 250862458 .

[25] Пендри, Дж.Б.; Шуриг, Д.; Смит, Д.Р. (8 декабря 2009 г.). «Аппарат, методы и системы электромагнитного сжатия» . Патентное ведомство США. Патент США 7629941 – через Google Patents.

[shalaev2007-26] Шалаев, В.М. (2007). «Оптические метаматериалы с отрицательным преломлением». Природная фотоника . 1 (1): 41–48. Бибкод : 2007NaPho...1...41S . дои : 10.1038/nphoton.2006.49 . S2CID 170678 .

[Feynman,_Richard_P._2011-27] Перейти обратно: ^а ^б Фейнман, Ричард П. (2011). В основном механика, радиация и тепло . Фейнмановские лекции по физике. Том. 1 (изд. «Новое тысячелетие»). Основные книги. ISBN 978-0-465-02493-3 .

[dispersion_ELPT-28] Перейти обратно: ^а ^б Пашотта, Рюдигер. «Хроматическая дисперсия» . Энциклопедия фотоники RP . Архивировано из оригинала 29 июня 2015 г. Проверено 13 августа 2023 г.

[hyperphysics_dispersion-29] Перейти обратно: ^а ^б Нейв, Карл Р. (2000). «Рассеивание» . Гиперфизика . Кафедра физики и астрономии Университета штата Джорджия. Архивировано из оригинала 24 сентября 2014 г. Проверено 13 августа 2023 г.

[30] Пашотта, Рюдигер. «Формула Зельмейера» . Энциклопедия фотоники RP . Архивировано из оригинала 19 марта 2015 г. Проверено 8 сентября 2014 г.

[31] Компания Шотт. «Интерактивная диаграмма Аббе» . Шотт.com . Проверено 13 августа 2023 г.

[32] Корпорация Охара. «Оптические свойства» . Охаракорп.com . Проверено 15 августа 2022 г.

[33] Группа Хойя. «Оптические свойства» . Оптическое подразделение Hoya Group . Проверено 13 августа 2023 г.

[34] Лентес, Франк-Томас; Клемент, Марк К.Т.; Нейрот, Норберт; Хоффманн, Ханс-Юрген; Хайден, Юико Т.; Хайден, Джозеф С.; Кольберг, Уве; Вольф, Силке (1998). «Оптические свойства». У Баха, Ганс; Нейрот, Норберт (ред.). Свойства оптического стекла . Серия Шотта о стекле и стеклокерамике. п. 30. дои : 10.1007/978-3-642-57769-7 . ISBN 978-3-642-63349-2 .

[35] Крей, Стефан; Прочь, Деннис; Рупрехт, Айко (08 марта 2014 г.). «Измерение показателя преломления прецизионными гониометрами: сравнительное исследование» . В Соскинде Яков Григорьевич; Олсон, Крейг (ред.). Учеб. SPIE 8992, Фотонное приборостроение . SPIE OPTO, 2014. Том. 8992. Сан-Франциско, Калифорния: SPIE. стр. 56–65. Бибкод : 2014SPIE.8992E..0DK . дои : 10.1117/12.2041760 . S2CID 120544352 .

[36] Рупп, Фабиан; Джедамзик, Ральф; Бартелмесс, Лотар; Петцольд, Уве (12 сентября 2021 г.). «Современный способ измерения показателя преломления оптического стекла в компании SCHOTT» . В Фелькеле, Рейнхард; Гейл, Роланд; Отадуй, Дейце (ред.). Оптическое производство, испытания и метрология VII . Том. 11873. ШПИОН. стр. 15–22. Бибкод : 2021SPIE11873E..08R . дои : 10.1117/12.2597023 . ISBN 9781510645905 . S2CID 240561530 . {{cite book}}: |journal= игнорируется ( помогите )

[37] «Рефрактометр Аббе | ATAGO CO., LTD» . www.atago.net . Проверено 15 августа 2022 г.

[38] «Многоволновой рефрактометр Аббе» . Нова-Тек Интернешнл . Проверено 15 августа 2022 г.

[39] Бах, Ганс; Нейрот, Норберт, ред. (1998). Свойства оптического стекла . Серия Шотта о стекле и стеклокерамике. п. 267. дои : 10.1007/978-3-642-57769-7 . ISBN 978-3-642-63349-2 .

[40] Дрессельхаус, MS (1999). «Физика твердого тела, часть II. Оптические свойства твердых тел» (PDF) . Курс 6.732 Физика твердого тела . Массачусетский технологический институт. Архивировано (PDF) из оригинала 24 июля 2015 г. Проверено 5 января 2015 г.

[41] Р. Пашотта, статья об оптической толщине. Архивировано 22 марта 2015 г. на Wayback Machine в Энциклопедии лазерной физики и технологий. Архивировано 13 августа 2015 г. на Wayback Machine , доступ 8 сентября 2014 г.

[42] Р. Пашотта, статья о рефракции. Архивировано 28 июня 2015 г. в Wayback Machine в Энциклопедии лазерной физики и технологий. Архивировано 13 августа 2015 г. в Wayback Machine , доступ: 8 сентября 2014 г.

[bornwolf-43] Перейти обратно: ^а ^б ^с ^д Борн, Макс ; Вольф, Эмиль (1999). Принципы оптики (7-е расширенное изд.). Архив Кубка. п. 22 . ISBN 978-0-521-78449-8 .

[44] Пашотта, Р. «Полное внутреннее отражение» . Энциклопедия фотоники RP . Архивировано из оригинала 28 июня 2015 г. Проверено 16 августа 2015 г.

[ri-min-45] Свенсон, Джим (10 ноября 2009 г.). «Показатель преломления минералов» . Ньютон BBS / Аргоннская национальная лаборатория. Министерство энергетики США. Архивировано из оригинала 28 мая 2010 года . Проверено 28 июля 2010 г. Включает материалы, являющиеся общественным достоянием Министерства энергетики США.

[46] Нейв, Карл Р. «Формула производителей линз» . Гиперфизика . Кафедра физики и астрономии. Государственный университет Джорджии. Архивировано из оригинала 26 сентября 2014 г. Проверено 8 сентября 2014 г.

[Carlsson-47] Перейти обратно: ^а ^б ^с Карлссон, Кьелл (2007). Световая микроскопия (PDF) (Отчет). Архивировано (PDF) из оригинала 2 апреля 2015 г. Проверено 2 января 2015 г.

[bleaney-48] Блини, Б .; Блини, Б.И. (1976). Электричество и магнетизм (Третье изд.). Издательство Оксфордского университета . ISBN 978-0-19-851141-0 .

[49] Эндрюс, Дэвид Л. (24 февраля 2015 г.). Фотоника, Том 2: Нанофотонные структуры и материалы . Джон Уайли и сыновья. п. 54. ИСБН 978-1-118-22551-6 .

[50] Вутен, Фредерик (1972). Оптические свойства твердых тел . Нью-Йорк: Академическая пресса . п. 49. ИСБН 978-0-12-763450-0 . (онлайн-pdf) Архивировано 3 октября 2011 г. в Wayback Machine.

[51] «Расчет показателя преломления стекол» . Статистический расчет и определение свойств стекла . Архивировано из оригинала 15 октября 2007 г.

[52] Стоун, Джек А.; Циммерман, Джей Х. (28 декабря 2011 г.). «Показатель преломления воздуха» . Инструментарий инженерной метрологии . Национальный институт стандартов и технологий (NIST). Архивировано из оригинала 11 января 2014 г. Проверено 11 января 2014 г.

[53] Ландольт, Х. (январь 1862 г.). «О показателях преломления жидких гомологичных соединений» . Анналы физики . 193 (11): 353–385. дои : 10.1002/andp.18621931102 . ISSN 0003-3804 .

[54] Ландольт, Х. (январь 1864 г.). «О влиянии атомистического состава С, Н и Осодержащих жидких соединений на распространение света» . Анналы физики . 199 (12): 595–628. дои : 10.1002/andp.18641991206 . ISSN 0003-3804 .

[55] Бор, З.; Освай, К.; Рац, Б.; Сабо, Г. (1990). «Измерение группового показателя преломления интерферометром Майкельсона». Оптические коммуникации . 78 (2): 109–112. Бибкод : 1990OptCo..78..109B . дои : 10.1016/0030-4018(90)90104-2 .

[56] Милонни, Питер В.; Бойд, Роберт В. (31 декабря 2010 г.). «Импульс света в диэлектрической среде» . Достижения оптики и фотоники . 2 (4): 519. Бибкод : 2010AdOP....2..519M . дои : 10.1364/AOP.2.000519 . ISSN 1943-8206 .

[57] Янг, AT (2011). «Преломление воздуха» . Архивировано из оригинала 10 января 2015 года . Проверено 31 июля 2014 г.

[58] Баррелл, Х.; Сирс, Дж. Э. (1939). «Преломление и дисперсия воздуха для видимого спектра» . Философские труды Лондонского королевского общества . А. Математические и физические науки. 238 (786): 1–64. Бибкод : 1939RSPTA.238....1B . дои : 10.1098/rsta.1939.0004 . JSTOR 91351 .

[59] Апарисио, Хосеп М.; Ларош, Стефан (2 июня 2011 г.). «Оценка проявления атмосферной рефракции для сигналов GPS» . Журнал геофизических исследований . 116 (Д11): Д11104. Бибкод : 2011JGRD..11611104A . дои : 10.1029/2010JD015214 .

[60] Сиддор, ЧП (1996). «Показатель преломления воздуха: новые уравнения для видимого и ближнего инфракрасного диапазона». Прикладная оптика . 35 (9): 1566–1573. Бибкод : 1996ApOpt..35.1566C . дои : 10.1364/ao.35.001566 . ПМИД 21085275 .

[61] Р. Пашотта, статья о двойном лучепреломлении. Архивировано 3 июля 2015 г. в Wayback Machine в Энциклопедии лазерной физики и технологий. Архивировано 13 августа 2015 г. в Wayback Machine , по состоянию на 9 сентября 2014 г.

[62] «Эволюция рефрактометра Аббе» . Государственный университет Гумбольдта, Ричард А. Паселк. 1998. Архивировано из оригинала 12 июня 2011 г. Проверено 3 сентября 2011 г.

[63] «Рефрактометры и рефрактометрия» . Рефрактометр.пл. 2011. Архивировано из оригинала 20 октября 2011 г. Проверено 3 сентября 2011 г.

[64] «Рефрактометр» . Геммологический проект. Архивировано из оригинала 10 сентября 2011 г. Проверено 3 сентября 2011 г.

[65] Фицджеральд, Ричард (июль 2000 г.). «Фазочувствительная рентгеновская визуализация» . Физика сегодня . 53 (7): 23. Бибкод : 2000ФТ....53г..23Ф . дои : 10.1063/1.1292471 . S2CID 121322301 .

[1]

[2]

[3]

[4]

[5]

[6]

[7]

[8]

[9]

[10]

[11]

[12]

[13]

[14]

[15]

[16]

[17]

[18]

[19]

[20]

[а]

[21]

[22]

[23]

[24]

[25]

[26]

[27]

[28]

[29]

[30]

[31]

[32]

[33]

[34]

[35]

[36]

[37]

[38]

[39]

[40]

[41]

[42]

[43]

[44]

[45]

[46]

[47]

[48]

[49]

[50]

[51]

[52]

[53]

[54]

[55]

[56]

[57]

[58]

[59]

[60]

[61]

[62]

[63]

[64]