Nelson rules
Nelson rules are a method in process control of determining whether some measured variable is out of control (unpredictable versus consistent). Rules for detecting "out-of-control" or non-random conditions were first postulated by Walter A. Shewhart[1] in the 1920s. The Nelson rules were first published in the October 1984 issue of the Journal of Quality Technology in an article by Lloyd S Nelson.[2]
The rules are applied to a control chart on which the magnitude of some variable is plotted against time. The rules are based on the mean value and the standard deviation of the samples.
| Rule | Description | Chart Example | Problem Indicated |
|---|---|---|---|
Rule 1 |
One point is more than 3 standard deviations from the mean. |  |
One sample (two shown in this case) is grossly out of control. |
Rule 2 |
Nine (or more) points in a row are on the same side of the mean. | 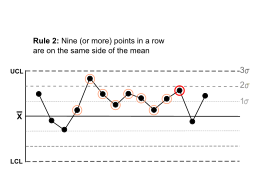 |
Some prolonged bias exists. |
Rule 3 |
Six (or more) points in a row are continually increasing (or decreasing). | A trend exists. | |
Rule 4 |
Fourteen (or more) points in a row alternate in direction, increasing then decreasing. | 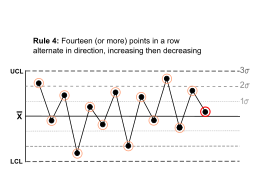 |
This much oscillation is beyond noise.
Note that the rule is concerned with directionality only. The position of the mean and the size of the standard deviation have no bearing. |
Rule 5 |
Two (or three) out of three points in a row are more than 2 standard deviations from the mean in the same direction. |  |
There is a medium tendency for samples to be mediumly out of control.
The side of the mean for the third point is unspecified. |
Rule 6 |
Four (or five) out of five points in a row are more than 1 standard deviation from the mean in the same direction. | 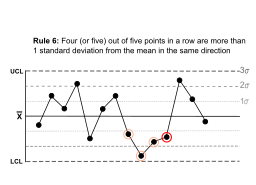 |
There is a strong tendency for samples to be slightly out of control.
The side of the mean for the fifth point is unspecified. |
Rule 7 |
Fifteen points in a row are all within 1 standard deviation of the mean on either side of the mean. | 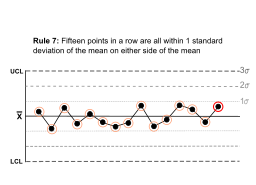 |
With 1 standard deviation, greater variation would be expected. |
Rule 8 |
Eight points in a row exist, but none within 1 standard deviation of the mean, and the points are in both directions from the mean. | 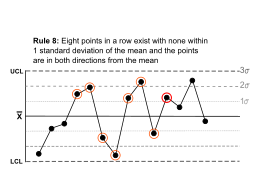 |
Jumping from above to below while missing the first standard deviation band is rarely random. |
The above eight rules apply to a chart of a variable value.
A second chart, the moving range chart, can also be used but only with rules 1, 2, 3 and 4. Such a chart plots a graph of the maximum value - minimum value of N adjacent points against the time sample of the range.
An example moving range: if N = 3 and values are 1, 3, 5, 3, 3, 2, 4, 5 then the sets of adjacent points are (1,3,5) (3,5,3) (5,3,3) (3,3,2) (3,2,4) (2,4,5) resulting in moving range values of (5-1) (5-3) (5-3) (3-2) (4-2) (5-2) = 4, 2, 2, 1, 2, 3.
Applying these rules indicates when a potential "out of control" situation has arisen. However, there will always be some false alerts and the more rules applied the more will occur. For some processes, it may be beneficial to omit one or more rules. Equally there may be some missing alerts where some specific "out of control" situation is not detected. Empirically, the detection accuracy is good.
See also
[edit]- Common cause and special cause
- Statistical process control
- Western Electric rules
- Westgard rules
- American Society for Quality, Quality Tools
References
[edit]- ^ Engineering Statistics Handbook 6.3.2, NIST/SEMATECH e-Handbook of Statistical Methods National Institute of Standards and Technology, Dec 2006
- ^ Lloyd S. Nelson, "The Shewhart Control Chart—Tests for Special Causes". Journal of Quality Technology 16, no. 4 (October 1984), 238-239. https://doi.org/10.1080/00224065.1984.11978921
