Jump to content

Octadecagon

From Wikipedia, the free encyclopedia
(Redirected from Regular octadecagon)
Regular octadecagon
A regular octadecagon
TypeRegular polygon
Edges and vertices18
Schläfli symbol{18}, t{9}
Coxeter–Dynkin diagrams
Symmetry groupDihedral (D18), order 2×18
Internal angle (degrees)160°
PropertiesConvex, cyclic, equilateral, isogonal, isotoxal
Dual polygonSelf

In geometry, an octadecagon (or octakaidecagon[1]) or 18-gon is an eighteen-sided polygon.[2]

Regular octadecagon

[edit]
Octadecagon with all 135 diagonals

A regular octadecagon has a Schläfli symbol {18} and can be constructed as a quasiregular truncated enneagon, t{9}, which alternates two types of edges.

Construction

[edit]

As 18 = 2 × 32, a regular octadecagon cannot be constructed using a compass and straightedge.[3] However, it is constructible using neusis, or an angle trisection with a tomahawk.

Octadecagon, an exact construction based on the angle trisection 120° by means of the tomahawk, animation 1 min 34 s.

The following approximate construction is very similar to that of the enneagon, as an octadecagon can be constructed as a truncated enneagon. It is also feasible with exclusive use of compass and straightedge.

Downsize the angle AMC (also 60°) with four angle bisectors and make a thirds of circular arc MON with an approximate solution between angle bisectors w3 and w4.
Straight auxiliary line g aims over the point O to the point N (virtually a ruler at the points O and N applied), between O and N, therefore no auxiliary line.
Thus, the circular arc MON is freely accessible for the later intersection point R.
AMR = 19.999999994755615...°
360° ÷ 18 = 20°
AMR - 20° = -5.244...E-9°
Example to illustrate the error:
At a circumscribed circle radius r = 100,000 km, the absolute error of the 1st side would be approximately -9 mm.
See also the calculation nanogan (Berechnung, German)
6.0 JMR equivalent AMR.

Symmetry

[edit]
Symmetries of a regular octadecagon. Vertices are colored by their symmetry positions. Blue mirrors are drawn through vertices, and purple mirrors are drawn through edge. Gyration orders are given in the center.

The regular octadecagon has Dih18 symmetry, order 36. There are 5 subgroup dihedral symmetries: Dih9, (Dih6, Dih3), and (Dih2 Dih1), and 6 cyclic group symmetries: (Z18, Z9), (Z6, Z3), and (Z2, Z1).

These 15 symmetries can be seen in 12 distinct symmetries on the octadecagon. John Conway labels these by a letter and group order.[4] Full symmetry of the regular form is r36 and no symmetry is labeled a1. The dihedral symmetries are divided depending on whether they pass through vertices (d for diagonal) or edges (p for perpendiculars), and i when reflection lines path through both edges and vertices. Cyclic symmetries in the middle column are labeled as g for their central gyration orders.

Each subgroup symmetry allows one or more degrees of freedom for irregular forms. Only the g18 subgroup has no degrees of freedom but can be seen as directed edges.

Dissection

[edit]
18-gon with 144 rhombs
An equilateral pentagonal dissection, with sequential internal angles: 60°, 160°, 80°, 100°, and 140°. Each of the 24 pentagons can be seen as the union of an equilateral triangle and an 80° rhombus.[5]

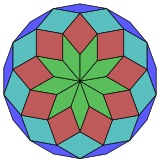
Coxeter states that every zonogon (a 2m-gon whose opposite sides are parallel and of equal length) can be dissected into m(m-1)/2 parallelograms.[6] In particular this is true for regular polygons with evenly many sides, in which case the parallelograms are all rhombi. For the regular octadecagon, m=9, and it can be divided into 36: 4 sets of 9 rhombs. This decomposition is based on a Petrie polygon projection of a 9-cube, with 36 of 4608 faces. The list OEIS: A006245 enumerates the number of solutions as 112018190, including up to 18-fold rotations and chiral forms in reflection.

Dissection into 36 rhombs

Uses

[edit]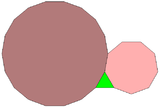


A regular triangle, nonagon, and octadecagon can completely surround a point in the plane, one of 17 different combinations of regular polygons with this property.[7] However, this pattern cannot be extended to an Archimedean tiling of the plane: because the triangle and the nonagon both have an odd number of sides, neither of them can be completely surrounded by a ring alternating the other two kinds of polygon.

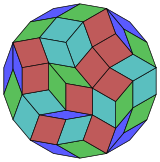
The regular octadecagon can tessellate the plane with concave hexagonal gaps. And another tiling mixes in nonagons and octagonal gaps. The first tiling is related to a truncated hexagonal tiling, and the second the truncated trihexagonal tiling.

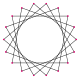
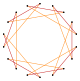
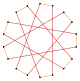
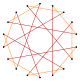
[edit]

An octadecagram is an 18-sided star polygon, represented by symbol {18/n}. There are two regular star polygons: {18/5} and {18/7}, using the same points, but connecting every fifth or seventh points. There are also five compounds: {18/2} is reduced to 2{9} or two enneagons, {18/3} is reduced to 3{6} or three hexagons, {18/4} and {18/8} are reduced to 2{9/2} and 2{9/4} or two enneagrams, {18/6} is reduced to 6{3} or 6 equilateral triangles, and finally {18/9} is reduced to 9{2} as nine digons.

Deeper truncations of the regular enneagon and enneagrams can produce isogonal (vertex-transitive) intermediate octadecagram forms with equally spaced vertices and two edge lengths. Other truncations form double coverings: t{9/8}={18/8}=2{9/4}, t{9/4}={18/4}=2{9/2}, t{9/2}={18/2}=2{9}.[8]

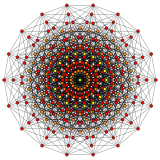
Petrie polygons

[edit]

A regular skew octadecagon is the Petrie polygon for a number of higher-dimensional polytopes, shown in these skew orthogonal projections from Coxeter planes:

References

[edit]
  1. ^ Kinsey, L. Christine; Moore, Teresa E. (2002), Symmetry, Shape, and Surfaces: An Introduction to Mathematics Through Geometry, Springer, p. 86, ISBN 9781930190092.
  2. ^ Adams, Henry (1907), Cassell's Engineer's Handbook: Comprising Facts and Formulæ, Principles and Practice, in All Branches of Engineering, D. McKay, p. 528.
  3. ^ Conway, John B. (2010), Mathematical Connections: A Capstone Course, American Mathematical Society, p. 31, ISBN 9780821849798.
  4. ^ John H. Conway, Heidi Burgiel, Chaim Goodman-Strauss, (2008) The Symmetries of Things, ISBN 978-1-56881-220-5 (Chapter 20, Generalized Schaefli symbols, Types of symmetry of a polygon pp. 275-278)
  5. ^ Hirschhorn & Hunt 1985.
  6. ^ Coxeter, Mathematical recreations and Essays, Thirteenth edition, p.141
  7. ^ Dallas, Elmslie William (1855), The Elements of Plane Practical Geometry, Etc, John W. Parker & Son, p. 134.
  8. ^ The Lighter Side of Mathematics: Proceedings of the Eugène Strens Memorial Conference on Recreational Mathematics and its History, (1994), Metamorphoses of polygons, Branko Grünbaum
[edit]
Retrieved from "https://en.wikipedia.org/w/index.php?title=Octadecagon&oldid=1197675000"