Uniform tilings in hyperbolic plane
| Spherical | Euclidean | Hyperbolic | |||
|---|---|---|---|---|---|
 {5,3} 5.5.5    
|
 {6,3} 6.6.6 
|
 {7,3} 7.7.7 
|
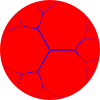 {∞,3} ∞.∞.∞ 
| ||
| Regular tilings {p,q} of the sphere, Euclidean plane, and hyperbolic plane using regular pentagonal, hexagonal and heptagonal and apeirogonal faces. | |||||
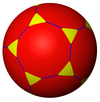 t{5,3} 10.10.3
|
 t{6,3} 12.12.3
|
 t{7,3} 14.14.3
|
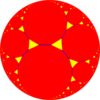 t{∞,3} ∞.∞.3
| ||
| Truncated tilings have 2p.2p.q vertex figures from regular {p,q}. | |||||
 r{5,3} 3.5.3.5
|
 r{6,3} 3.6.3.6
|
 r{7,3} 3.7.3.7
|
 r{∞,3} 3.∞.3.∞
| ||
| Quasiregular tilings are similar to regular tilings but alternate two types of regular polygon around each vertex. | |||||
 rr{5,3} 3.4.5.4
|
 rr{6,3} 3.4.6.4
|
 rr{7,3} 3.4.7.4
|
 rr{∞,3} 3.4.∞.4
| ||
| Semiregular tilings have more than one type of regular polygon. | |||||
 tr{5,3} 4.6.10
|
 tr{6,3} 4.6.12
|
 tr{7,3} 4.6.14
|
 tr{∞,3} 4.6.∞
| ||
| Omnitruncated tilings have three or more even-sided regular polygons. | |||||
| Symmetry | Triangular dihedral symmetry
|
Tetrahedral
|
Octahedral
|
Icosahedral
|
p6m symmetry
|
[3,7] symmetry
|
[3,8] symmetry
| |||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Starting solid Operation |
Symbol {p,q}  
|
Triangular hosohedron {2,3}  |
Triangular dihedron {3,2}  |
Tetrahedron {3,3}  |
Cube {4,3}  |
Octahedron {3,4}  |
Dodecahedron {5,3}  |
Icosahedron {3,5}  |
Hexagonal tiling {6,3}  |
Triangular tiling {3,6}  |
Heptagonal tiling {7,3} |
Order-7 triangular tiling {3,7}  |
Octagonal tiling {8,3}  |
Order-8 triangular tiling {3,8} 
|
| Truncation (t) | t{p,q}
|
triangular prism |
truncated triangular dihedron (Half of the "edges" count as degenerate digon faces. The other half are normal edges.) |
truncated tetrahedron |
truncated cube |
truncated octahedron |
truncated dodecahedron |
truncated icosahedron |
Truncated hexagonal tiling |
Truncated triangular tiling |
Truncated heptagonal tiling |
Truncated order-7 triangular tiling |
Truncated octagonal tiling |
Truncated order-8 triangular tiling
|
| Rectification (r) Ambo (a) |
r{p,q}
|
tridihedron(All of the "edges" count as degenerate digon faces.) |
tetratetrahedron |
cuboctahedron |
icosidodecahedron |
Trihexagonal tiling |
Triheptagonal tiling |
Trioctagonal tiling
| ||||||
| Bitruncation (2t) Dual kis (dk) |
2t{p,q}
|
truncated triangular dihedron(Half of the "edges" count as degenerate digon faces. The other half are normal edges.) |
triangular prism |
truncated tetrahedron |
truncated octahedron |
truncated cube |
truncated icosahedron |
truncated dodecahedron |
truncated triangular tiling |
truncated hexagonal tiling |
Truncated order-7 triangular tiling |
Truncated heptagonal tiling |
Truncated order-8 triangular tiling |
Truncated octagonal tiling
|
| Birectification (2r) Dual (d) |
2r{p,q}
|
triangular dihedron {3,2} |
triangular hosohedron {2,3} |
tetrahedron |
octahedron |
cube |
icosahedron |
dodecahedron |
triangular tiling |
hexagonal tiling |
Order-7 triangular tiling |
Heptagonal tiling |
Order-8 triangular tiling |
Octagonal tiling
|
| Cantellation (rr) Expansion (e) |
rr{p,q}
|
triangular prism(The "edge" between each pair of tetragons counts as a degenerate digon face. The other edges (the ones between a trigon and a tetragon) are normal edges.) |
rhombitetratetrahedron |
rhombicuboctahedron |
rhombicosidodecahedron  |
rhombitrihexagonal tiling |
Rhombitriheptagonal tiling  |
Rhombitrioctagonal tiling 
| ||||||
| Snub rectified (sr) Snub (s) |
sr{p,q}
|
triangular antiprism (Three yellow-yellow "edges", no two of which share any vertices, count as degenerate digon faces. The other edges are normal edges.) |
snub tetratetrahedron |
snub cuboctahedron |
snub icosidodecahedron |
snub trihexagonal tiling |
Snub triheptagonal tiling |
Snub trioctagonal tiling
| ||||||
| Cantitruncation (tr) Bevel (b) |
tr{p,q}
|
hexagonal prism |
truncated tetratetrahedron |
truncated cuboctahedron |
truncated icosidodecahedron |
truncated trihexagonal tiling |
Truncated triheptagonal tiling |
Truncated trioctagonal tiling
| ||||||
In hyperbolic geometry, a uniform hyperbolic tiling (or regular, quasiregular or semiregular hyperbolic tiling) is an edge-to-edge filling of the hyperbolic plane which has regular polygons as faces and is vertex-transitive (transitive on its vertices, isogonal, i.e. there is an isometry mapping any vertex onto any other). It follows that all vertices are congruent, and the tiling has a high degree of rotational and translational symmetry.
Uniform tilings can be identified by their vertex configuration, a sequence of numbers representing the number of sides of the polygons around each vertex. For example, 7.7.7 represents the heptagonal tiling which has 3 heptagons around each vertex. It is also regular since all the polygons are the same size, so it can also be given the Schläfli symbol {7,3}.
Uniform tilings may be regular (if also face- and edge-transitive), quasi-regular (if edge-transitive but not face-transitive) or semi-regular (if neither edge- nor face-transitive). For right triangles (p q 2), there are two regular tilings, represented by Schläfli symbol {p,q} and {q,p}.
Wythoff construction
[edit]
There are an infinite number of uniform tilings based on the Schwarz triangles (p q r) where 1/p + 1/q + 1/r < 1, where p, q, r are each orders of reflection symmetry at three points of the fundamental domain triangle – the symmetry group is a hyperbolic triangle group.
Each symmetry family contains 7 uniform tilings, defined by a Wythoff symbol or Coxeter-Dynkin diagram, 7 representing combinations of 3 active mirrors. An 8th represents an alternation operation, deleting alternate vertices from the highest form with all mirrors active.
Families with r = 2 contain regular hyperbolic tilings, defined by a Coxeter group such as [7,3], [8,3], [9,3], ... [5,4], [6,4], ....
Hyperbolic families with r = 3 or higher are given by (p q r) and include (4 3 3), (5 3 3), (6 3 3) ... (4 4 3), (5 4 3), ... (4 4 4)....
Hyperbolic triangles (p q r) define compact uniform hyperbolic tilings. In the limit any of p, q or r can be replaced by ∞ which defines a paracompact hyperbolic triangle and creates uniform tilings with either infinite faces (called apeirogons) that converge to a single ideal point, or infinite vertex figure with infinitely many edges diverging from the same ideal point.
More symmetry families can be constructed from fundamental domains that are not triangles.
Selected families of uniform tilings are shown below (using the Poincaré disk model for the hyperbolic plane). Three of them – (7 3 2), (5 4 2), and (4 3 3) – and no others, are minimal in the sense that if any of their defining numbers is replaced by a smaller integer the resulting pattern is either Euclidean or spherical rather than hyperbolic; conversely, any of the numbers can be increased (even to infinity) to generate other hyperbolic patterns.
Each uniform tiling generates a dual uniform tiling, with many of them also given below.
Right triangle domains
[edit]There are infinitely many (p q 2) triangle group families. This article shows the regular tiling up to p, q = 8, and uniform tilings in 12 families: (7 3 2), (8 3 2), (5 4 2), (6 4 2), (7 4 2), (8 4 2), (5 5 2), (6 5 2) (6 6 2), (7 7 2), (8 6 2), and (8 8 2).
Regular hyperbolic tilings
[edit]
The simplest set of hyperbolic tilings are regular tilings {p,q}, which exist in a matrix with the regular polyhedra and Euclidean tilings. The regular tiling {p,q} has a dual tiling {q,p} across the diagonal axis of the table. Self-dual tilings {2,2}, {3,3}, {4,4}, {5,5}, etc. pass down the diagonal of the table.
| Regular hyperbolic tiling table | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Spherical (improper/Platonic)/Euclidean/hyperbolic (Poincaré disc: compact/paracompact/noncompact) tessellations with their Schläfli symbol | |||||||||||
| p \ q | 2 | 3 | 4 | 5 | 6 | 7 | 8 | ... | ∞ | ... | iπ/λ |
| 2 |  {2,2} 
|
{2,3}
|
 {2,4} 
|
 {2,5}
|
 {2,6}
|
 {2,7}
|
 {2,8} 
|
 {2,∞}
|
 {2,iπ/λ} 
| ||
| 3 |  {3,2}
|
 (tetrahedron) {3,3}
|
 (octahedron) {3,4}
|
 (icosahedron) {3,5}
|
 (deltille) {3,6}
|
 {3,7}
|
 {3,8}
|
 {3,∞}
|
 {3,iπ/λ}
| ||
| 4 |  {4,2}
|
 (cube) {4,3}
|
 (quadrille) {4,4}
|
 {4,5}
|
 {4,6}
|
 {4,7}
|
 {4,8}
|
 {4,∞}
|
 {4,iπ/λ}
| ||
| 5 |  {5,2}
|
(dodecahedron) {5,3}
|
 {5,4}
|
 {5,5}
|
 {5,6}
|
 {5,7}
|
 {5,8}
|
 {5,∞}
|
 {5,iπ/λ}
| ||
| 6 |  {6,2}
|
(hextille) {6,3}
|
 {6,4}
|
 {6,5}
|
 {6,6}
|
 {6,7}
|
 {6,8}
|
 {6,∞}
|
 {6,iπ/λ}
| ||
| 7 | {7,2}
|
{7,3}
|
 {7,4}
|
 {7,5}
|
 {7,6}
|
 {7,7}
|
 {7,8}
|
 {7,∞}
|
{7,iπ/λ}
| ||
| 8 | {8,2}
|
 {8,3}
|
 {8,4}
|
 {8,5}
|
 {8,6}
|
 {8,7}
|
 {8,8}
|
 {8,∞}
|
{8,iπ/λ}
| ||
| ... | |||||||||||
| ∞ |  {∞,2}
|
{∞,3}
|
 {∞,4}
|
 {∞,5}
|
 {∞,6}
|
 {∞,7}
|
 {∞,8}
|
 {∞,∞}
|
 {∞,iπ/λ}
| ||
| ... | |||||||||||
| iπ/λ |  {iπ/λ,2}
|
 {iπ/λ,3}
|
 {iπ/λ,4}
|
 {iπ/λ,5}
|
 {iπ/λ,6}
|
{iπ/λ,7}
|
{iπ/λ,8}
|
 {iπ/λ,∞}
|
{iπ/λ, iπ/λ} | ||
(7 3 2)
[edit]The (7 3 2) triangle group, Coxeter group [7,3], orbifold (*732) contains these uniform tilings:
| Uniform heptagonal/triangular tilings | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Symmetry: [7,3], (*732) | [7,3]+, (732) | ||||||||||
|
|
|
|
|
|
|
|
| ||||
|
|
|
|
|
|
|
|
| ||||
| {7,3} | t{7,3} | r{7,3} | t{3,7} | {3,7} | rr{7,3} | tr{7,3} | sr{7,3} | ||||
| Uniform duals | |||||||||||
|
|
|
|
|
|
|
| ||||
|
|
|
|
|
|
|
|
| ||||
| V73 | V3.14.14 | V3.7.3.7 | V6.6.7 | V37 | V3.4.7.4 | V4.6.14 | V3.3.3.3.7 | ||||
(8 3 2)
[edit]The (8 3 2) triangle group, Coxeter group [8,3], orbifold (*832) contains these uniform tilings:
| Uniform octagonal/triangular tilings | |||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Symmetry: [8,3], (*832) | [8,3]+ (832) |
[1+,8,3] (*443) |
[8,3+] (3*4) | ||||||||||
| {8,3} | t{8,3} | r{8,3} | t{3,8} | {3,8} | rr{8,3} s2{3,8} |
tr{8,3} | sr{8,3} | h{8,3} | h2{8,3} | s{3,8} | |||
|
|
|
|
|
|
|
|
|
| |||||
   
|
|
|
|
  or 
|
or
|
| |||||||
|
|
|
 
|
 
|
 
|
|
|
|
 
|
 
|
 
| |||
| Uniform duals | |||||||||||||
| V83 | V3.16.16 | V3.8.3.8 | V6.6.8 | V38 | V3.4.8.4 | V4.6.16 | V34.8 | V(3.4)3 | V8.6.6 | V35.4 | |||
|
|
|
|
|
|
|
|
|
|
|
| |||
|
|
|
|
|
|
|
|
|
|
|
| |||
(5 4 2)
[edit]The (5 4 2) triangle group, Coxeter group [5,4], orbifold (*542) contains these uniform tilings:
| Uniform pentagonal/square tilings | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Symmetry: [5,4], (*542) | [5,4]+, (542) | [5+,4], (5*2) | [5,4,1+], (*552) | ||||||||
|
|
|
|
|
|
|
|
|
|
| ||
|
|
|
|
|
|
|
|
|
|
| ||
| {5,4} | t{5,4} | r{5,4} | 2t{5,4}=t{4,5} | 2r{5,4}={4,5} | rr{5,4} | tr{5,4} | sr{5,4} | s{5,4} | h{4,5} | ||
| Uniform duals | |||||||||||
|
|
|
|
|
|
|
|
|
|
| ||
|
|
|
|
|
|
|
|
|
| |||
| V54 | V4.10.10 | V4.5.4.5 | V5.8.8 | V45 | V4.4.5.4 | V4.8.10 | V3.3.4.3.5 | V3.3.5.3.5 | V55 | ||
(6 4 2)
[edit]The (6 4 2) triangle group, Coxeter group [6,4], orbifold (*642) contains these uniform tilings. Because all the elements are even, each uniform dual tiling one represents the fundamental domain of a reflective symmetry: *3333, *662, *3232, *443, *222222, *3222, and *642 respectively. As well, all 7 uniform tiling can be alternated, and those have duals as well.
| Uniform tetrahexagonal tilings | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Symmetry: [6,4], (*642) (with [6,6] (*662), [(4,3,3)] (*443) , [∞,3,∞] (*3222) index 2 subsymmetries) (And [(∞,3,∞,3)] (*3232) index 4 subsymmetry) | |||||||||||
=    =  = 
|
= 
|
= =  =
|
=
|
= = = 
|
=
|
| |||||
|
|
|
|
|
|
| |||||
| {6,4} | t{6,4} | r{6,4} | t{4,6} | {4,6} | rr{6,4} | tr{6,4} | |||||
| Uniform duals | |||||||||||
|
|
|
|
|
|
|
| |||||
|
|
|
|
|
|
| |||||
| V64 | V4.12.12 | V(4.6)2 | V6.8.8 | V46 | V4.4.4.6 | V4.8.12 | |||||
| Alternations | |||||||||||
| [1+,6,4] (*443) |
[6+,4] (6*2) |
[6,1+,4] (*3222) |
[6,4+] (4*3) |
[6,4,1+] (*662) |
[(6,4,2+)] (2*32) |
[6,4]+ (642) | |||||
=
|
= 
|
=  
|
=
|
= 
|
= 
|
| |||||
|
|
|
|
|
|
| |||||
| h{6,4} | s{6,4} | hr{6,4} | s{4,6} | h{4,6} | hrr{6,4} | sr{6,4} | |||||
(7 4 2)
[edit]The (7 4 2) triangle group, Coxeter group [7,4], orbifold (*742) contains these uniform tilings:
| Uniform heptagonal/square tilings | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Symmetry: [7,4], (*742) | [7,4]+, (742) | [7+,4], (7*2) | [7,4,1+], (*772) | ||||||||
|
|
|
|
|
|
|
|
|
|
| ||
|
|
|
|
|
|
|
|
|
|
| ||
| {7,4} | t{7,4} | r{7,4} | 2t{7,4}=t{4,7} | 2r{7,4}={4,7} | rr{7,4} | tr{7,4} | sr{7,4} | s{7,4} | h{4,7} | ||
| Uniform duals | |||||||||||
|
|
|
|
|
|
|
|
|
|
| ||
|
|
|
|
|
|
|
|
| ||||
| V74 | V4.14.14 | V4.7.4.7 | V7.8.8 | V47 | V4.4.7.4 | V4.8.14 | V3.3.4.3.7 | V3.3.7.3.7 | V77 | ||
(8 4 2)
[edit]The (8 4 2) triangle group, Coxeter group [8,4], orbifold (*842) contains these uniform tilings. Because all the elements are even, each uniform dual tiling one represents the fundamental domain of a reflective symmetry: *4444, *882, *4242, *444, *22222222, *4222, and *842 respectively. As well, all 7 uniform tiling can be alternated, and those have duals as well.
| Uniform octagonal/square tilings | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| [8,4], (*842) (with [8,8] (*882), [(4,4,4)] (*444) , [∞,4,∞] (*4222) index 2 subsymmetries) (And [(∞,4,∞,4)] (*4242) index 4 subsymmetry) | |||||||||||
=  = = 
|
=
|
= = =
|
=
|
= =
|
=
|
| |||||
|
|
|
|
|
|
| |||||
| {8,4} | t{8,4} |
r{8,4} | 2t{8,4}=t{4,8} | 2r{8,4}={4,8} | rr{8,4} | tr{8,4} | |||||
| Uniform duals | |||||||||||
|
|
|
|
|
|
|
| |||||
|
|
|
|
|
|
| |||||
| V84 | V4.16.16 | V(4.8)2 | V8.8.8 | V48 | V4.4.4.8 | V4.8.16 | |||||
| Alternations | |||||||||||
| [1+,8,4] (*444) |
[8+,4] (8*2) |
[8,1+,4] (*4222) |
[8,4+] (4*4) |
[8,4,1+] (*882) |
[(8,4,2+)] (2*42) |
[8,4]+ (842) | |||||
=
|
= 
|
=
|
=
|
=
|
=
|
| |||||
|
|
|
|
|
|
| |||||
| h{8,4} | s{8,4} | hr{8,4} | s{4,8} | h{4,8} | hrr{8,4} | sr{8,4} | |||||
| Alternation duals | |||||||||||
|
|
|
|
|
|
|
| |||||
|
|
|
|
|
|||||||
| V(4.4)4 | V3.(3.8)2 | V(4.4.4)2 | V(3.4)3 | V88 | V4.44 | V3.3.4.3.8 | |||||
(5 5 2)
[edit]The (5 5 2) triangle group, Coxeter group [5,5], orbifold (*552) contains these uniform tilings:
| Uniform pentapentagonal tilings | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Symmetry: [5,5], (*552) | [5,5]+, (552) | ||||||||||
=
|
=
|
=
|
=
|
=
|
=
|
=
|
=
| ||||
|
|
|
|
|
|
|
|
| ||||
| Order-5 pentagonal tiling {5,5} |
Truncated order-5 pentagonal tiling t{5,5} |
Order-4 pentagonal tiling r{5,5} |
Truncated order-5 pentagonal tiling 2t{5,5} = t{5,5} |
Order-5 pentagonal tiling 2r{5,5} = {5,5} |
Tetrapentagonal tiling rr{5,5} |
Truncated order-4 pentagonal tiling tr{5,5} |
Snub pentapentagonal tiling sr{5,5} | ||||
| Uniform duals | |||||||||||
|
|
|
|
|
|
|
|
| ||||
|
|
|
|
|
|
|
|
|||||
| Order-5 pentagonal tiling V5.5.5.5.5 |
V5.10.10 | Order-5 square tiling V5.5.5.5 |
V5.10.10 | Order-5 pentagonal tiling V5.5.5.5.5 |
V4.5.4.5 | V4.10.10 | V3.3.5.3.5 | ||||
(6 5 2)
[edit]The (6 5 2) triangle group, Coxeter group [6,5], orbifold (*652) contains these uniform tilings:
| Uniform hexagonal/pentagonal tilings | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Symmetry: [6,5], (*652) | [6,5]+, (652) | [6,5+], (5*3) | [1+,6,5], (*553) | ||||||||
|
|
|
|
|
|
|
|
|
|
| ||
|
|
|
|
|
|
|
|
| |||
| {6,5} | t{6,5} | r{6,5} | 2t{6,5}=t{5,6} | 2r{6,5}={5,6} | rr{6,5} | tr{6,5} | sr{6,5} | s{5,6} | h{6,5} | ||
| Uniform duals | |||||||||||
|
|
|
|
|
|
|
|
|
|
| ||
|
|
|
|
|
|
|
|||||
| V65 | V5.12.12 | V5.6.5.6 | V6.10.10 | V56 | V4.5.4.6 | V4.10.12 | V3.3.5.3.6 | V3.3.3.5.3.5 | V(3.5)5 | ||
(6 6 2)
[edit]The (6 6 2) triangle group, Coxeter group [6,6], orbifold (*662) contains these uniform tilings:
| Uniform hexahexagonal tilings | ||||||
|---|---|---|---|---|---|---|
| Symmetry: [6,6], (*662) | ||||||
=   =
|
= =
|
= =
|
=  =
|
= =
|
= =
|
= =
|
|
|
|
|
|
|
|
| {6,6} = h{4,6} |
t{6,6} = h2{4,6} |
r{6,6} {6,4} |
t{6,6} = h2{4,6} |
{6,6} = h{4,6} |
rr{6,6} r{6,4} |
tr{6,6} t{6,4} |
| Uniform duals | ||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| V66 | V6.12.12 | V6.6.6.6 | V6.12.12 | V66 | V4.6.4.6 | V4.12.12 |
| Alternations | ||||||
| [1+,6,6] (*663) |
[6+,6] (6*3) |
[6,1+,6] (*3232) |
[6,6+] (6*3) |
[6,6,1+] (*663) |
[(6,6,2+)] (2*33) |
[6,6]+ (662) |
| =
|
|
=
|
|
= 
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| ||
| h{6,6} | s{6,6} | hr{6,6} | s{6,6} | h{6,6} | hrr{6,6} | sr{6,6} |
(8 6 2)
[edit]The (8 6 2) triangle group, Coxeter group [8,6], orbifold (*862) contains these uniform tilings.
| Uniform octagonal/hexagonal tilings | ||||||
|---|---|---|---|---|---|---|
| Symmetry: [8,6], (*862) | ||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| {8,6} | t{8,6} |
r{8,6} | 2t{8,6}=t{6,8} | 2r{8,6}={6,8} | rr{8,6} | tr{8,6} |
| Uniform duals | ||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| V86 | V6.16.16 | V(6.8)2 | V8.12.12 | V68 | V4.6.4.8 | V4.12.16 |
| Alternations | ||||||
| [1+,8,6] (*466) |
[8+,6] (8*3) |
[8,1+,6] (*4232) |
[8,6+] (6*4) |
[8,6,1+] (*883) |
[(8,6,2+)] (2*43) |
[8,6]+ (862) |
|
|
|
|
|
|
|
|
|
|
| ||||
| h{8,6} | s{8,6} | hr{8,6} | s{6,8} | h{6,8} | hrr{8,6} | sr{8,6} |
| Alternation duals | ||||||
|
|
|
|
|
|
|
|
|
||||||
| V(4.6)6 | V3.3.8.3.8.3 | V(3.4.4.4)2 | V3.4.3.4.3.6 | V(3.8)8 | V3.45 | V3.3.6.3.8 |
(7 7 2)
[edit]The (7 7 2) triangle group, Coxeter group [7,7], orbifold (*772) contains these uniform tilings:
| Uniform heptaheptagonal tilings | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Symmetry: [7,7], (*772) | [7,7]+, (772) | ||||||||||
=  =
|
= =
|
= =
|
= =
|
= =
|
= =
|
= =
|
= =
| ||||
|
|
|
|
|
|
|
|
| ||||
| {7,7} | t{7,7} |
r{7,7} | 2t{7,7}=t{7,7} | 2r{7,7}={7,7} | rr{7,7} | tr{7,7} | sr{7,7} | ||||
| Uniform duals | |||||||||||
|
|
|
|
|
|
|
|
| ||||
|
|
|
|
|
|
|
|
|||||
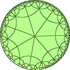
| V77 | V7.14.14 | V7.7.7.7 | V7.14.14 | V77 | V4.7.4.7 | V4.14.14 | V3.3.7.3.7 | ||||
(8 8 2)
[edit]The (8 8 2) triangle group, Coxeter group [8,8], orbifold (*882) contains these uniform tilings:
| Uniform octaoctagonal tilings | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Symmetry: [8,8], (*882) | |||||||||||
=  =
|
= =
|
= =
|
= =
|
= =
|
= =
|
= =
| |||||
|
|
|
|
|
|
| |||||
| {8,8} | t{8,8} |
r{8,8} | 2t{8,8}=t{8,8} | 2r{8,8}={8,8} | rr{8,8} | tr{8,8} | |||||
| Uniform duals | |||||||||||
|
|
|
|
|
|
|
| |||||
|
|
|
|
|
|
| |||||
| V88 | V8.16.16 | V8.8.8.8 | V8.16.16 | V88 | V4.8.4.8 | V4.16.16 | |||||
| Alternations | |||||||||||
| [1+,8,8] (*884) |
[8+,8] (8*4) |
[8,1+,8] (*4242) |
[8,8+] (8*4) |
[8,8,1+] (*884) |
[(8,8,2+)] (2*44) |
[8,8]+ (882) | |||||
| =
|
|
=
|
|
=
|
= =
|
= =
| |||||
|
|
|
|
| |||||||
| h{8,8} | s{8,8} | hr{8,8} | s{8,8} | h{8,8} | hrr{8,8} | sr{8,8} | |||||
| Alternation duals | |||||||||||
|
|
|
|
|
|
|
| |||||
|
|
|
||||||||||
| V(4.8)8 | V3.4.3.8.3.8 | V(4.4)4 | V3.4.3.8.3.8 | V(4.8)8 | V46 | V3.3.8.3.8 | |||||
General triangle domains
[edit]There are infinitely many general triangle group families (p q r). This article shows uniform tilings in 9 families: (4 3 3), (4 4 3), (4 4 4), (5 3 3), (5 4 3), (5 4 4), (6 3 3), (6 4 3), and (6 4 4).
(4 3 3)
[edit]The (4 3 3) triangle group, Coxeter group [(4,3,3)], orbifold (*433) contains these uniform tilings. Without right angles in the fundamental triangle, the Wythoff constructions are slightly different. For instance in the (4,3,3) triangle family, the snub form has six polygons around a vertex and its dual has hexagons rather than pentagons. In general the vertex figure of a snub tiling in a triangle (p,q,r) is p. 3.q.3.r.3, being 4.3.3.3.3.3 in this case below.
| Symmetry: [(4,3,3)], (*433) | [(4,3,3)]+, (433) | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|
|
|
|
|
|
|
|
|
| |||
|
|
|
|
|
|
|
|
| |||
|
|
|
|
|
|
|
| |||
| h{8,3} t0(4,3,3) |
r{3,8}1/2 t0,1(4,3,3) |
h{8,3} t1(4,3,3) |
h2{8,3} t1,2(4,3,3) |
{3,8}1/2 t2(4,3,3) |
h2{8,3} t0,2(4,3,3) |
t{3,8}1/2 t0,1,2(4,3,3) |
s{3,8}1/2 s(4,3,3) | |||
| Uniform duals | ||||||||||
|
|
|
|
|
|
|
|
| |||
| V(3.4)3 | V3.8.3.8 | V(3.4)3 | V3.6.4.6 | V(3.3)4 | V3.6.4.6 | V6.6.8 | V3.3.3.3.3.4 | |||
(4 4 3)
[edit]The (4 4 3) triangle group, Coxeter group [(4,4,3)], orbifold (*443) contains these uniform tilings.
| Uniform (4,4,3) tilings | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Symmetry: [(4,4,3)] (*443) | [(4,4,3)]+ (443) |
[(4,4,3+)] (3*22) |
[(4,1+,4,3)] (*3232) | |||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| h{6,4} t0(4,4,3) |
h2{6,4} t0,1(4,4,3) |
{4,6}1/2 t1(4,4,3) |
h2{6,4} t1,2(4,4,3) |
h{6,4} t2(4,4,3) |
r{6,4}1/2 t0,2(4,4,3) |
t{4,6}1/2 t0,1,2(4,4,3) |
s{4,6}1/2 s(4,4,3) |
hr{4,6}1/2 hr(4,3,4) |
h{4,6}1/2 h(4,3,4) |
q{4,6} h1(4,3,4) |
| Uniform duals | ||||||||||
|
|
|
|
|
|||||||
| V(3.4)4 | V3.8.4.8 | V(4.4)3 | V3.8.4.8 | V(3.4)4 | V4.6.4.6 | V6.8.8 | V3.3.3.4.3.4 | V(4.4.3)2 | V66 | V4.3.4.6.6 |
(4 4 4)
[edit]The (4 4 4) triangle group, Coxeter group [(4,4,4)], orbifold (*444) contains these uniform tilings.
| Uniform (4,4,4) tilings | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Symmetry: [(4,4,4)], (*444) | [(4,4,4)]+ (444) |
[(1+,4,4,4)] (*4242) |
[(4+,4,4)] (4*22) | ||||||||
|
|
|
|
|
|
|
|
|
|
| ||
|
|
|
|
|
|
|
|
|
| ||
| t0(4,4,4) h{8,4} |
t0,1(4,4,4) h2{8,4} |
t1(4,4,4) {4,8}1/2 |
t1,2(4,4,4) h2{8,4} |
t2(4,4,4) h{8,4} |
t0,2(4,4,4) r{4,8}1/2 |
t0,1,2(4,4,4) t{4,8}1/2 |
s(4,4,4) s{4,8}1/2 |
h(4,4,4) h{4,8}1/2 |
hr(4,4,4) hr{4,8}1/2 | ||
| Uniform duals | |||||||||||
|
|
|
|
|
|
|
|
|
| ||
| V(4.4)4 | V4.8.4.8 | V(4.4)4 | V4.8.4.8 | V(4.4)4 | V4.8.4.8 | V8.8.8 | V3.4.3.4.3.4 | V88 | V(4,4)3 | ||
(5 3 3)
[edit]The (5 3 3) triangle group, Coxeter group [(5,3,3)], orbifold (*533) contains these uniform tilings.
| Uniform (5,3,3) tilings | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Symmetry: [(5,3,3)], (*533) | [(5,3,3)]+, (533) | ||||||||||
|
|
|
|
|
|
|
| ||||
|
|
|
|
|
|
|
| ||||
|
|
|
|
|
|
|
| ||||
| h{10,3} t0(5,3,3) |
r{3,10}1/2 t0,1(5,3,3) |
h{10,3} t1(5,3,3) |
h2{10,3} t1,2(5,3,3) |
{3,10}1/2 t2(5,3,3) |
h2{10,3} t0,2(5,3,3) |
t{3,10}1/2 t0,1,2(5,3,3) |
s{3,10}1/2 ht0,1,2(5,3,3) | ||||
| Uniform duals | |||||||||||
|
|
||||||||||
| V(3.5)3 | V3.10.3.10 | V(3.5)3 | V3.6.5.6 | V(3.3)5 | V3.6.5.6 | V6.6.10 | V3.3.3.3.3.5 | ||||
(5 4 3)
[edit]The (5 4 3) triangle group, Coxeter group [(5,4,3)], orbifold (*543) contains these uniform tilings.
| (5,4,3) uniform tilings | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Symmetry: [(5,4,3)], (*543) | [(5,4,3)]+, (543) | ||||||||||
|
|
|
|
|
|
|
| ||||
|
|
|
|
|
|
|
| ||||
| t0(5,4,3) (5,4,3) |
t0,1(5,4,3) r(3,5,4) |
t1(5,4,3) (4,3,5) |
t1,2(5,4,3) r(5,4,3) |
t2(5,4,3) (3,5,4) |
t0,2(5,4,3) r(4,3,5) |
t0,1,2(5,4,3) t(5,4,3) |
s(5,4,3) | ||||
| Uniform duals | |||||||||||
|
|||||||||||
| V(3.5)4 | V3.10.4.10 | V(4.5)3 | V3.8.5.8 | V(3.4)5 | V4.6.5.6 | V6.8.10 | V3.5.3.4.3.3 | ||||
(5 4 4)
[edit]The (5 4 4) triangle group, Coxeter group [(5,4,4)], orbifold (*544) contains these uniform tilings.
| Uniform (5,4,4) tilings | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Symmetry: [(5,4,4)] (*544) |
[(5,4,4)]+ (544) |
[(5+,4,4)] (5*22) |
[(5,4,1+,4)] (*5222) | ||||||||
|
|
|
|
|
|
|
|
|
|
| ||
|
|
|
|
|
|
|
|
|
|
| ||
|
|
|
|
|
|
|
|
||||
| t0(5,4,4) h{10,4} |
t0,1(5,4,4) r{4,10}1/2 |
t1(5,4,4) h{10,4} |
t1,2(5,4,4) h2{10,4} |
t2(5,4,4) {4,10}1/2 |
t0,2(5,4,4) h2{10,4} |
t0,1,2(5,4,4) t{4,10}1/2 |
s(4,5,4) s{4,10}1/2 |
h(4,5,4) h{4,10}1/2 |
hr(4,5,4) hr{4,10}1/2 | ||
| Uniform duals | |||||||||||
|
|
|
|||||||||
| V(4.5)4 | V4.10.4.10 | V(4.5)4 | V4.8.5.8 | V(4.4)5 | V4.8.5.8 | V8.8.10 | V3.4.3.4.3.5 | V1010 | V(4.4.5)2 | ||
(6 3 3)
[edit]The (6 3 3) triangle group, Coxeter group [(6,3,3)], orbifold (*633) contains these uniform tilings.
| Uniform (6,3,3) tilings | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Symmetry: [(6,3,3)], (*633) | [(6,3,3)]+, (633) | ||||||||||
|
|
|
|
|
|
|
| ||||
|
|
|
|
|
|
|
| ||||
|
|
|
|
|
|
|
| ||||
| t0{(6,3,3)} h{12,3} |
t0,1{(6,3,3)} r{3,12}1/2 |
t1{(6,3,3)} h{12,3} |
t1,2{(6,3,3)} h2{12,3} |
t2{(6,3,3)} {3,12}1/2 |
t0,2{(6,3,3)} h2{12,3} |
t0,1,2{(6,3,3)} t{3,12}1/2 |
s{(6,3,3)} s{3,12}1/2 | ||||
| Uniform duals | |||||||||||
|
|
||||||||||
| V(3.6)3 | V3.12.3.12 | V(3.6)3 | V3.6.6.6 | V(3.3)6 {12,3} |
V3.6.6.6 | V6.6.12 | V3.3.3.3.3.6 | ||||
(6 4 3)
[edit]The (6 4 3) triangle group, Coxeter group [(6,4,3)], orbifold (*643) contains these uniform tilings.
| (6,4,3) uniform tilings | |||||||||
|---|---|---|---|---|---|---|---|---|---|
| Symmetry: [(6,4,3)] (*643) |
[(6,4,3)]+ (643) |
[(6,1+,4,3)] (*3332) |
[(6,4,3+)] (3*32) | ||||||
|
|
|
|
|
|
|
|
= 
|
|
|
|
|
|
|
|
|
|
||
| t0{(6,4,3)} | t0,1{(6,4,3)} | t1{(6,4,3)} | t1,2{(6,4,3)} | t2{(6,4,3)} | t0,2{(6,4,3)} | t0,1,2{(6,4,3)} | s{(6,4,3)} | h{(6,4,3)} | hr{(6,4,3)} |
| Uniform duals | |||||||||
|
|
|
|||||||
| V(3.6)4 | V3.12.4.12 | V(4.6)3 | V3.8.6.8 | V(3.4)6 | V4.6.6.6 | V6.8.12 | V3.6.3.4.3.3 | V(3.6.6)3 | V4.(3.4)3 |
(6 4 4)
[edit]The (6 4 4) triangle group, Coxeter group [(6,4,4)], orbifold (*644) contains these uniform tilings.
| 6-4-4 uniform tilings | |||||||
|---|---|---|---|---|---|---|---|
| Symmetry: [(6,4,4)], (*644) | (644) | ||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| (6,4,4) h{12,4} |
t0,1(6,4,4) r{4,12}1/2 |
t1(6,4,4) h{12,4} |
t1,2(6,4,4) h2{12,4} |
t2(6,4,4) {4,12}1/2 |
t0,2(6,4,4) h2{12,4} |
t0,1,2(6,4,4) t{4,12}1/2 |
s(6,4,4) s{4,12}1/2 |
| Uniform duals | |||||||
|
|
|
|
|
|
|
|
| V(4.6)4 | V(4.12)2 | V(4.6)4 | V4.8.6.8 | V412 | V4.8.6.8 | V8.8.12 | V4.6.4.6.6.6 |
Summary of tilings with finite triangular fundamental domains
[edit]For a table of all uniform hyperbolic tilings with fundamental domains (p q r), where 2 ≤ p,q,r ≤ 8.
Quadrilateral domains
[edit]
(3 2 2 2)
[edit]
Quadrilateral fundamental domains also exist in the hyperbolic plane, with the *3222 orbifold ([∞,3,∞] Coxeter notation) as the smallest family. There are 9 generation locations for uniform tiling within quadrilateral domains. The vertex figure can be extracted from a fundamental domain as 3 cases (1) Corner (2) Mid-edge, and (3) Center. When generating points are corners adjacent to order-2 corners, degenerate {2} digon faces at those corners exist but can be ignored. Snub and alternated uniform tilings can also be generated (not shown) if a vertex figure contains only even-sided faces.
Coxeter diagrams of quadrilateral domains are treated as a degenerate tetrahedron graph with 2 of 6 edges labeled as infinity, or as dotted lines. A logical requirement of at least one of two parallel mirrors being active limits the uniform cases to 9, and other ringed patterns are not valid.
| Uniform tilings in symmetry *3222 | ||||
|---|---|---|---|---|
| 64
|
 6.6.4.4.png)
|
 (3.4.4)2
|
4.3.4.3.3.3
| |
6.6.4.4
|
6.4.4.4
|
3.4.4.4.4.png)
| ||
| (3.4.4)2
|
3.4.4.4.4
|
46
| ||
(3 2 3 2)
[edit]| Similar H2 tilings in *3232 symmetry | ||||||||
|---|---|---|---|---|---|---|---|---|
| Coxeter diagrams |
|
|
|
| ||||
 |
|
|
|
|
|
|
| |
|
|
|
|
| |||||
| Vertex figure |
66 | (3.4.3.4)2 | 3.4.6.6.4 | 6.4.6.4 | ||||
| Image | 
|
|
|
| ||||
| Dual | 
|
| ||||||
Ideal triangle domains
[edit]There are infinitely many triangle group families including infinite orders. This article shows uniform tilings in 9 families: (∞ 3 2), (∞ 4 2), (∞ ∞ 2), (∞ 3 3), (∞ 4 3), (∞ 4 4), (∞ ∞ 3), (∞ ∞ 4), and (∞ ∞ ∞).
(∞ 3 2)
[edit]The ideal (∞ 3 2) triangle group, Coxeter group [∞,3], orbifold (*∞32) contains these uniform tilings:
| Paracompact uniform tilings in [∞,3] family | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Symmetry: [∞,3], (*∞32) | [∞,3]+ (∞32) |
[1+,∞,3] (*∞33) |
[∞,3+] (3*∞) | |||||||
|
|
|
|
|
|
|
|
|
|
|
|
= 
|
=
|
=
|
|
= or
|
= or
|
=
| ||||
|
|
|
|
|
|
|
|
|
|
| |
| {∞,3} | t{∞,3} | r{∞,3} | t{3,∞} | {3,∞} | rr{∞,3} | tr{∞,3} | sr{∞,3} | h{∞,3} | h2{∞,3} | s{3,∞} |
| Uniform duals | ||||||||||
|
|
|
|
|
|
|
|
|
|
| |
|
|
|
|
|
|
|
|
|
|
||
| V∞3 | V3.∞.∞ | V(3.∞)2 | V6.6.∞ | V3∞ | V4.3.4.∞ | V4.6.∞ | V3.3.3.3.∞ | V(3.∞)3 | V3.3.3.3.3.∞ | |
(∞ 4 2)
[edit]The ideal (∞ 4 2) triangle group, Coxeter group [∞,4], orbifold (*∞42) contains these uniform tilings:
| Paracompact uniform tilings in [∞,4] family | |||||||
|---|---|---|---|---|---|---|---|
|
|
|
|
|
|
|
| |
|
|
|
|
|
|
|
| |
| {∞,4} | t{∞,4} | r{∞,4} | 2t{∞,4}=t{4,∞} | 2r{∞,4}={4,∞} | rr{∞,4} | tr{∞,4} | |
| Dual figures | |||||||
|
|
|
|
|
|
|
| |
|
|
|
|
|
|
| |
| V∞4 | V4.∞.∞ | V(4.∞)2 | V8.8.∞ | V4∞ | V43.∞ | V4.8.∞ | |
| Alternations | |||||||
| [1+,∞,4] (*44∞) |
[∞+,4] (∞*2) |
[∞,1+,4] (*2∞2∞) |
[∞,4+] (4*∞) |
[∞,4,1+] (*∞∞2) |
[(∞,4,2+)] (2*2∞) |
[∞,4]+ (∞42) | |
=
|
|
|
|
= 
|
|
| |
| h{∞,4} | s{∞,4} | hr{∞,4} | s{4,∞} | h{4,∞} | hrr{∞,4} | s{∞,4} | |
|
|
|
| ||||
| Alternation duals | |||||||
|
|
|
|
|
|
|
| |
|
|
||||||
| V(∞.4)4 | V3.(3.∞)2 | V(4.∞.4)2 | V3.∞.(3.4)2 | V∞∞ | V∞.44 | V3.3.4.3.∞ | |
(∞ 5 2)
[edit]The ideal (∞ 5 2) triangle group, Coxeter group [∞,5], orbifold (*∞52) contains these uniform tilings:
| Paracompact uniform apeirogonal/pentagonal tilings | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Symmetry: [∞,5], (*∞52) | [∞,5]+ (∞52) |
[1+,∞,5] (*∞55) |
[∞,5+] (5*∞) | ||||||||
|
|
|
|
|
|
|
|
|
|
|
| |
|
|
|
|
|
|
|
|
|
|
|||
| {∞,5} | t{∞,5} | r{∞,5} | 2t{∞,5}=t{5,∞} | 2r{∞,5}={5,∞} | rr{∞,5} | tr{∞,5} | sr{∞,5} | h{∞,5} | h2{∞,5} | s{5,∞} | |
| Uniform duals | |||||||||||
|
|
|
|
|
|
|
|
|
|
|
| |
|
|
|
|
||||||||
| V∞5 | V5.∞.∞ | V5.∞.5.∞ | V∞.10.10 | V5∞ | V4.5.4.∞ | V4.10.∞ | V3.3.5.3.∞ | V(∞.5)5 | V3.5.3.5.3.∞ | ||
(∞ ∞ 2)
[edit]The ideal (∞ ∞ 2) triangle group, Coxeter group [∞,∞], orbifold (*∞∞2) contains these uniform tilings:
| Paracompact uniform tilings in [∞,∞] family | ||||||
|---|---|---|---|---|---|---|
= =
|
= =
|
= = 
|
= =
|
= =
|
=
|
=
|
|
|
|
|
|
|
|
|
| {∞,∞} | t{∞,∞} | r{∞,∞} | 2t{∞,∞}=t{∞,∞} | 2r{∞,∞}={∞,∞} | rr{∞,∞} | tr{∞,∞} |
| Dual tilings | ||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| V∞∞ | V∞.∞.∞ | V(∞.∞)2 | V∞.∞.∞ | V∞∞ | V4.∞.4.∞ | V4.4.∞ |
| Alternations | ||||||
| [1+,∞,∞] (*∞∞2) |
[∞+,∞] (∞*∞) |
[∞,1+,∞] (*∞∞∞∞) |
[∞,∞+] (∞*∞) |
[∞,∞,1+] (*∞∞2) |
[(∞,∞,2+)] (2*∞∞) |
[∞,∞]+ (2∞∞) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| |
| h{∞,∞} | s{∞,∞} | hr{∞,∞} | s{∞,∞} | h2{∞,∞} | hrr{∞,∞} | sr{∞,∞} |
| Alternation duals | ||||||
|
|
|
|
|
|
|
|
|
|
|
|
| |||
| V(∞.∞)∞ | V(3.∞)3 | V(∞.4)4 | V(3.∞)3 | V∞∞ | V(4.∞.4)2 | V3.3.∞.3.∞ |
(∞ 3 3)
[edit]The ideal (∞ 3 3) triangle group, Coxeter group [(∞,3,3)], orbifold (*∞33) contains these uniform tilings.
| Paracompact hyperbolic uniform tilings in [(∞,3,3)] family | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Symmetry: [(∞,3,3)], (*∞33) | [(∞,3,3)]+, (∞33) | ||||||||||
|
|
|
|
|
|
|
|
| ||||
|
|
|
|
|
|
|
|
| ||||
|
|
|
|
|
|
|
|
| ||||
| (∞,∞,3) | t0,1(∞,3,3) | t1(∞,3,3) | t1,2(∞,3,3) | t2(∞,3,3) | t0,2(∞,3,3) | t0,1,2(∞,3,3) | s(∞,3,3) | ||||
| Dual tilings | |||||||||||
|
|
|
|
|
|
|
|
| ||||
|
|
|
|
|
|
|
|
| ||||
|
|
|
||||||||||
| V(3.∞)3 | V3.∞.3.∞ | V(3.∞)3 | V3.6.∞.6 | V(3.3)∞ | V3.6.∞.6 | V6.6.∞ | V3.3.3.3.3.∞ | ||||
(∞ 4 3)
[edit]The ideal (∞ 4 3) triangle group, Coxeter group [(∞,4,3)], orbifold (*∞43) contains these uniform tilings:
| Paracompact hyperbolic uniform tilings in [(∞,4,3)] family | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Symmetry: [(∞,4,3)] (*∞43) |
[(∞,4,3)]+ (∞43) |
[(∞,4,3+)] (3*4∞) |
[(∞,1+,4,3)] (*∞323) | ||||||||
|
|
|
|
|
|
|
|
|
= 
| ||
|
|
|
|
|
|
|
|
||||
| (∞,4,3) | t0,1(∞,4,3) | t1(∞,4,3) | t1,2(∞,4,3) | t2(∞,4,3) | t0,2(∞,4,3) | t0,1,2(∞,4,3) | s(∞,4,3) | ht0,2(∞,4,3) | ht1(∞,4,3) | ||
| Dual tilings | |||||||||||
|
|
|
|||||||||
| V(3.∞)4 | V3.∞.4.∞ | V(4.∞)3 | V3.8.∞.8 | V(3.4)∞ | 4.6.∞.6 | V6.8.∞ | V3.3.3.4.3.∞ | V(4.3.4)2.∞ | V(6.∞.6)3 | ||
(∞ 4 4)
[edit]The ideal (∞ 4 4) triangle group, Coxeter group [(∞,4,4)], orbifold (*∞44) contains these uniform tilings.
| Paracompact hyperbolic uniform tilings in [(4,4,∞)] family | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Symmetry: [(4,4,∞)], (*44∞) | (44∞) | ||||||||||
|
|
|
|
|
|
|
|
| ||||
|
|
|
|
|
|
|
|
| ||||
| (4,4,∞) h{∞,4} |
t0,1(4,4,∞) r{4,∞}1/2 |
t1(4,4,∞) h{4,∞}1/2 |
t1,2(4,4,∞) h2{∞,4} |
t2(4,4,∞) {4,∞}1/2 |
t0,2(4,4,∞) h2{∞,4} |
t0,1,2(4,4,∞) t{4,∞}1/2 |
s(4,4,∞) s{4,∞}1/2 | ||||
| Dual tilings | |||||||||||
|
|
|
|
|
|
|
|
|||||
| V(4.∞)4 | V4.∞.4.∞ | V(4.∞)4 | V4.∞.4.∞ | V4∞ | V4.∞.4.∞ | V8.8.∞ | V3.4.3.4.3.∞ | ||||
(∞ ∞ 3)
[edit]The ideal (∞ ∞ 3) triangle group, Coxeter group [(∞,∞,3)], orbifold (*∞∞3) contains these uniform tilings.
| Paracompact hyperbolic uniform tilings in [(∞,∞,3)] family | |||||||||
|---|---|---|---|---|---|---|---|---|---|
| Symmetry: [(∞,∞,3)], (*∞∞3) | [(∞,∞,3)]+ (∞∞3) |
[(∞,∞,3+)] (3*∞∞) |
[(∞,1+,∞,3)] (*∞3∞3) | ||||||
|
|
|
|
|
|
|
|
|
|
= 
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| |
| (∞,∞,3) h{6,∞} |
t0,1(∞,∞,3) h2{6,∞} |
t1(∞,∞,3) {∞,6}1/2 |
t1,2(∞,∞,3) h2{6,∞} |
t2(∞,∞,3) h{6,∞} |
t0,2(∞,∞,3) r{∞,6}1/2 |
t0,1,2(∞,∞,3) t{∞,6}1/2 |
s(∞,∞,3) s{∞,6}1/2 |
hr0,2(∞,∞,3) hr{∞,6}1/2 |
hr1(∞,∞,3) h{∞,6}1/2 |
| Dual tilings | |||||||||
|
|
|
| ||||||
| V(3.∞)∞ | V3.∞.∞.∞ | V(∞.∞)3 | V3.∞.∞.∞ | V(3.∞)∞ | V(6.∞)2 | V6.∞.∞ | V3.∞.3.∞.3.3 | V(3.4.∞.4)2 | V(∞.6)6 |
(∞ ∞ 4)
[edit]The ideal (∞ ∞ 4) triangle group, Coxeter group [(∞,∞,4)], orbifold (*∞∞4) contains these uniform tilings.
| Paracompact hyperbolic uniform tilings in [(∞,∞,4)] family | ||||||
|---|---|---|---|---|---|---|
| Symmetry: [(∞,∞,4)], (*∞∞4) | ||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| (∞,∞,4) h{8,∞} |
t0,1(∞,∞,4) h2{8,∞} |
t1(∞,∞,4) {∞,8} |
t1,2(∞,∞,4) h2{∞,8} |
t2(∞,∞,4) h{8,∞} |
t0,2(∞,∞,4) r{∞,8} |
t0,1,2(∞,∞,4) t{∞,8} |
| Dual tilings | ||||||
|
|
|
|
|
|
|
| V(4.∞)∞ | V∞.∞.∞.4 | V∞4 | V∞.∞.∞.4 | V(4.∞)∞ | V∞.∞.∞.4 | V∞.∞.8 |
| Alternations | ||||||
| [(1+,∞,∞,4)] (*2∞∞∞) |
[(∞+,∞,4)] (∞*2∞) |
[(∞,1+,∞,4)] (*2∞∞∞) |
[(∞,∞+,4)] (∞*2∞) |
[(∞,∞,1+,4)] (*2∞∞∞) |
[(∞,∞,4+)] (2*∞∞) |
[(∞,∞,4)]+ (4∞∞) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| |||
| Alternation duals | ||||||
|
|
|
|
||||
| V∞∞ | V∞.44 | V(∞.4)4 | V∞.44 | V∞∞ | V∞.44 | V3.∞.3.∞.3.4 |
(∞ ∞ ∞)
[edit]The ideal (∞ ∞ ∞) triangle group, Coxeter group [(∞,∞,∞)], orbifold (*∞∞∞) contains these uniform tilings.
| Paracompact uniform tilings in [(∞,∞,∞)] family | ||||||
|---|---|---|---|---|---|---|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| (∞,∞,∞) h{∞,∞} |
r(∞,∞,∞) h2{∞,∞} |
(∞,∞,∞) h{∞,∞} |
r(∞,∞,∞) h2{∞,∞} |
(∞,∞,∞) h{∞,∞} |
r(∞,∞,∞) r{∞,∞} |
t(∞,∞,∞) t{∞,∞} |
| Dual tilings | ||||||
|
|
|
|
|
|
|
| V∞∞ | V∞.∞.∞.∞ | V∞∞ | V∞.∞.∞.∞ | V∞∞ | V∞.∞.∞.∞ | V∞.∞.∞ |
| Alternations | ||||||
| [(1+,∞,∞,∞)] (*∞∞∞∞) |
[∞+,∞,∞)] (∞*∞) |
[∞,1+,∞,∞)] (*∞∞∞∞) |
[∞,∞+,∞)] (∞*∞) |
[(∞,∞,∞,1+)] (*∞∞∞∞) |
[(∞,∞,∞+)] (∞*∞) |
[∞,∞,∞)]+ (∞∞∞) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| Alternation duals | ||||||
|
|
|
|
|
|
|
|
| V(∞.∞)∞ | V(∞.4)4 | V(∞.∞)∞ | V(∞.4)4 | V(∞.∞)∞ | V(∞.4)4 | V3.∞.3.∞.3.∞ |
Summary of tilings with infinite triangular fundamental domains
[edit]For a table of all uniform hyperbolic tilings with fundamental domains (p q r), where 2 ≤ p,q,r ≤ 8, and one or more as ∞.
| Infinite triangular hyperbolic tilings | |||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| (p q r) | t0 | h0 | t01 | h01 | t1 | h1 | t12 | h12 | t2 | h2 | t02 | h02 | t012 | s | |||||
(∞ 3 2) |
t0{∞,3} ∞3 |
h0{∞,3} (3.∞)3 |
t01{∞,3} ∞.3.∞ |
t1{∞,3} (3.∞)2 |
t12{∞,3} 6.∞.6 |
h12{∞,3} 3.3.3.∞.3.3 |
t2{∞,3} 3∞ |
t02{∞,3} 3.4.∞.4 |
t012{∞,3} 4.6.∞ |
s{∞,3} 3.3.3.3.∞ | |||||||||
(∞ 4 2) |
t0{∞,4} ∞4 |
h0{∞,4} (4.∞)4 |
t01{∞,4} ∞.4.∞ |
h01{∞,4} 3.∞.3.3.∞ |
t1{∞,4} (4.∞)2 |
h1{∞,4} (4.4.∞)2 |
t12{∞,4} 8.∞.8 |
h12{∞,4} 3.4.3.∞.3.4 |
t2{∞,4} 4∞ |
h2{∞,4} ∞∞ |
t02{∞,4} 4.4.∞.4 |
h02{∞,4} 4.4.4.∞.4 |
t012{∞,4} 4.8.∞ |
s{∞,4} 3.3.4.3.∞ | |||||
(∞ 5 2) |
t0{∞,5} ∞5 |
h0{∞,5} (5.∞)5 |
t01{∞,5} ∞.5.∞ |
t1{∞,5} (5.∞)2 |
t12{∞,5} 10.∞.10 |
h12{∞,5} 3.5.3.∞.3.5 |
t2{∞,5} 5∞ |
t02{∞,5} 5.4.∞.4 |
t012{∞,5} 4.10.∞ |
s{∞,5} 3.3.5.3.∞ | |||||||||
 (∞ 6 2) |
t0{∞,6} ∞6 |
h0{∞,6} (6.∞)6 |
t01{∞,6} ∞.6.∞ |
h01{∞,6} 3.∞.3.3.3.∞ |
t1{∞,6} (6.∞)2 |
h1{∞,6} (4.3.4.∞)2 |
t12{∞,6} 12.∞.12 |
h12{∞,6} 3.6.3.∞.3.6 |
t2{∞,6} 6∞ |
h2{∞,6} (∞.3)∞ |
t02{∞,6} 6.4.∞.4 |
h02{∞,6} 4.3.4.4.∞.4 |
t012{∞,6} 4.12.∞ |
s{∞,6} 3.3.6.3.∞ | |||||
 (∞ 7 2) |
t0{∞,7} ∞7 |
h0{∞,7} (7.∞)7 |
t01{∞,7} ∞.7.∞ |
t1{∞,7} (7.∞)2 |
t12{∞,7} 14.∞.14 |
h12{∞,7} 3.7.3.∞.3.7 |
t2{∞,7} 7∞ |
t02{∞,7} 7.4.∞.4 |
t012{∞,7} 4.14.∞ |
s{∞,7} 3.3.7.3.∞ | |||||||||
 (∞ 8 2) |
t0{∞,8} ∞8 |
h0{∞,8} (8.∞)8 |
t01{∞,8} ∞.8.∞ |
h01{∞,8} 3.∞.3.4.3.∞ |
t1{∞,8} (8.∞)2 |
h1{∞,8} (4.4.4.∞)2 |
t12{∞,8} 16.∞.16 |
h12{∞,8} 3.8.3.∞.3.8 |
t2{∞,8} 8∞ |
h2{∞,8} (∞.4)∞ |
t02{∞,8} 8.4.∞.4 |
h02{∞,8} 4.4.4.4.∞.4 |
t012{∞,8} 4.16.∞ |
s{∞,8} 3.3.8.3.∞ | |||||
(∞ ∞ 2) |
t0{∞,∞} ∞∞ |
h0{∞,∞} (∞.∞)∞ |
t01{∞,∞} ∞.∞.∞ |
h01{∞,∞} 3.∞.3.∞.3.∞ |
t1{∞,∞} ∞4 |
h1{∞,∞} (4.∞)4 |
t12{∞,∞} ∞.∞.∞ |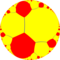
h12{∞,∞} 3.∞.3.∞.3.∞ |
t2{∞,∞} ∞∞ |
h2{∞,∞} (∞.∞)∞ |
t02{∞,∞} (∞.4)2 |
h02{∞,∞} (4.∞.4)2 |
t012{∞,∞} 4.∞.∞ |
s{∞,∞} 3.3.∞.3.∞ | |||||
(∞ 3 3) |
t0(∞,3,3) (∞.3)3 |
t01(∞,3,3) (3.∞)2 |
t1(∞,3,3) (3.∞)3 |
t12(∞,3,3) 3.6.∞.6 |
t2(∞,3,3) 3∞ |
t02(∞,3,3) 3.6.∞.6 |
t012(∞,3,3) 6.6.∞ |
s(∞,3,3) 3.3.3.3.3.∞ | |||||||||||
(∞ 4 3) |
t0(∞,4,3) (∞.3)4 |
t01(∞,4,3) 3.∞.4.∞ |
t1(∞,4,3) (4.∞)3 |
h1(∞,4,3) (6.6.∞)3 |
t12(∞,4,3) 3.8.∞.8 |
t2(∞,4,3) (4.3)∞ |
t02(∞,4,3) 4.6.∞.6 |
h02(∞,4,3) 4.4.3.4.∞.4.3 |
t012(∞,4,3) 6.8.∞ |
s(∞,4,3) 3.3.3.4.3.∞ | |||||||||
 (∞ 5 3) |
t0(∞,5,3) (∞.3)5 |
t01(∞,5,3) 3.∞.5.∞ |
t1(∞,5,3) (5.∞)3 |
t12(∞,5,3) 3.10.∞.10 |
t2(∞,5,3) (5.3)∞ |
t02(∞,5,3) 5.6.∞.6 |
t012(∞,5,3) 6.10.∞ |
s(∞,5,3) 3.3.3.5.3.∞ | |||||||||||
 (∞ 6 3) |
t0(∞,6,3) (∞.3)6 |
t01(∞,6,3) 3.∞.6.∞ |
t1(∞,6,3) (6.∞)3 |
h1(∞,6,3) (6.3.6.∞)3 |
t12(∞,6,3) 3.12.∞.12 |
t2(∞,6,3) (6.3)∞ |
t02(∞,6,3) 6.6.∞.6 |
h02(∞,6,3) 4.3.4.3.4.∞.4.3 |
t012(∞,6,3) 6.12.∞ |
s(∞,6,3) 3.3.3.6.3.∞ | |||||||||
 (∞ 7 3) |
t0(∞,7,3) (∞.3)7 |
t01(∞,7,3) 3.∞.7.∞ |
t1(∞,7,3) (7.∞)3 |
t12(∞,7,3) 3.14.∞.14 |
t2(∞,7,3) (7.3)∞ |
t02(∞,7,3) 7.6.∞.6 |
t012(∞,7,3) 6.14.∞ |
s(∞,7,3) 3.3.3.7.3.∞ | |||||||||||
 (∞ 8 3) |
t0(∞,8,3) (∞.3)8 |
t01(∞,8,3) 3.∞.8.∞ |
t1(∞,8,3) (8.∞)3 |
h1(∞,8,3) (6.4.6.∞)3 |
t12(∞,8,3) 3.16.∞.16 |
t2(∞,8,3) (8.3)∞ |
t02(∞,8,3) 8.6.∞.6 |
h02(∞,8,3) 4.4.4.3.4.∞.4.3 |
t012(∞,8,3) 6.16.∞ |
s(∞,8,3) 3.3.3.8.3.∞ | |||||||||
(∞ ∞ 3) |
t0(∞,∞,3) (∞.3)∞ |
t01(∞,∞,3) 3.∞.∞.∞ |
t1(∞,∞,3) ∞6 |
h1(∞,∞,3) (6.∞)6 |
t12(∞,∞,3) 3.∞.∞.∞ |
t2(∞,∞,3) (∞.3)∞ |
t02(∞,∞,3) (∞.6)2 |
h02(∞,∞,3) (4.∞.4.3)2 |
t012(∞,∞,3) 6.∞.∞ |
s(∞,∞,3) 3.3.3.∞.3.∞ | |||||||||
(∞ 4 4) |
t0(∞,4,4) (∞.4)4 |
h0(∞,4,4) (8.∞.8)4 |
t01(∞,4,4) (4.∞)2 |
h01(∞,4,4) (4.4.∞)2 |
t1(∞,4,4) (4.∞)4 |
h1(∞,4,4) (8.8.∞)4 |
t12(∞,4,4) 4.8.∞.8 |
h12(∞,4,4) 4.4.4.4.∞.4.4 |
t2(∞,4,4) 4∞ |
h2(∞,4,4) ∞∞ |
t02(∞,4,4) 4.8.∞.8 |
h02(∞,4,4) 4.4.4.4.∞.4.4 |
t012(∞,4,4) 8.8.∞ |
s(∞,4,4) 3.4.3.4.3.∞ | |||||
 (∞ 5 4) |
t0(∞,5,4) (∞.4)5 |
h0(∞,5,4) (10.∞.10)5 |
t01(∞,5,4) 4.∞.5.∞ |
t1(∞,5,4) (5.∞)4 |
t12(∞,5,4) 4.10.∞.10 |
h12(∞,5,4) 4.4.5.4.∞.4.5 |
t2(∞,5,4) (5.4)∞ |
t02(∞,5,4) 5.8.∞.8 |
t012(∞,5,4) 8.10.∞ |
s(∞,5,4) 3.4.3.5.3.∞ | |||||||||
 (∞ 6 4) |
t0(∞,6,4) (∞.4)6 |
h0(∞,6,4) (12.∞.12)6 |
t01(∞,6,4) 4.∞.6.∞ |
h01(∞,6,4) 4.4.∞.4.3.4.∞ |
t1(∞,6,4) (6.∞)4 |
h1(∞,6,4) (8.3.8.∞)4 |
t12(∞,6,4) 4.12.∞.12 |
h12(∞,6,4) 4.4.6.4.∞.4.6 |
t2(∞,6,4) (6.4)∞ |
h2(∞,6,4) (∞.3.∞)∞ |
t02(∞,6,4) 6.8.∞.8 |
h02(∞,6,4) 4.3.4.4.4.∞.4.4 |
t012(∞,6,4) 8.12.∞ |
s(∞,6,4) 3.4.3.6.3.∞ | |||||
 (∞ 7 4) |
t0(∞,7,4) (∞.4)7 |
h0(∞,7,4) (14.∞.14)7 |
t01(∞,7,4) 4.∞.7.∞ |
t1(∞,7,4) (7.∞)4 |
t12(∞,7,4) 4.14.∞.14 |
h12(∞,7,4) 4.4.7.4.∞.4.7 |
t2(∞,7,4) (7.4)∞ |
t02(∞,7,4) 7.8.∞.8 |
t012(∞,7,4) 8.14.∞ |
s(∞,7,4) 3.4.3.7.3.∞ | |||||||||
 (∞ 8 4) |
t0(∞,8,4) (∞.4)8 |
h0(∞,8,4) (16.∞.16)8 |
t01(∞,8,4) 4.∞.8.∞ |
h01(∞,8,4) 4.4.∞.4.4.4.∞ |
t1(∞,8,4) (8.∞)4 |
h1(∞,8,4) (8.4.8.∞)4 |
t12(∞,8,4) 4.16.∞.16 |
h12(∞,8,4) 4.4.8.4.∞.4.8 |
t2(∞,8,4) (8.4)∞ |
h2(∞,8,4) (∞.4.∞)∞ |
t02(∞,8,4) 8.8.∞.8 |
h02(∞,8,4) 4.4.4.4.4.∞.4.4 |
t012(∞,8,4) 8.16.∞ |
s(∞,8,4) 3.4.3.8.3.∞ | |||||
(∞ ∞ 4) |
t0(∞,∞,4) (∞.4)∞ |
h0(∞,∞,4) (∞.∞.∞)∞ |
t01(∞,∞,4) 4.∞.∞.∞ |
h01(∞,∞,4) 4.4.∞.4.∞.4.∞ |
t1(∞,∞,4) ∞8 |
h1(∞,∞,4) (8.∞)8 |
t12(∞,∞,4) 4.∞.∞.∞ |
h12(∞,∞,4) 4.4.∞.4.∞.4.∞ |
t2(∞,∞,4) (∞.4)∞ |
h2(∞,∞,4) (∞.∞.∞)∞ |
t02(∞,∞,4) (∞.8)2 |
h02(∞,∞,4) (4.∞.4.4)2 |
t012(∞,∞,4) 8.∞.∞ |
s(∞,∞,4) 3.4.3.∞.3.∞ | |||||
 (∞ 5 5) |
t0(∞,5,5) (∞.5)5 |
t01(∞,5,5) (5.∞)2 |
t1(∞,5,5) (5.∞)5 |
t12(∞,5,5) 5.10.∞.10 |
t2(∞,5,5) 5∞ |
t02(∞,5,5) 5.10.∞.10 |
t012(∞,5,5) 10.10.∞ |
s(∞,5,5) 3.5.3.5.3.∞ | |||||||||||
 (∞ 6 5) |
t0(∞,6,5) (∞.5)6 |
t01(∞,6,5) 5.∞.6.∞ |
t1(∞,6,5) (6.∞)5 |
h1(∞,6,5) (10.3.10.∞)5 |
t12(∞,6,5) 5.12.∞.12 |
t2(∞,6,5) (6.5)∞ |
t02(∞,6,5) 6.10.∞.10 |
h02(∞,6,5) 4.3.4.5.4.∞.4.5 |
t012(∞,6,5) 10.12.∞ |
s(∞,6,5) 3.5.3.6.3.∞ | |||||||||
 (∞ 7 5) |
t0(∞,7,5) (∞.5)7 |
t01(∞,7,5) 5.∞.7.∞ |
t1(∞,7,5) (7.∞)5 |
t12(∞,7,5) 5.14.∞.14 |
t2(∞,7,5) (7.5)∞ |
t02(∞,7,5) 7.10.∞.10 |
t012(∞,7,5) 10.14.∞ |
s(∞,7,5) 3.5.3.7.3.∞ | |||||||||||
 (∞ 8 5) |
t0(∞,8,5) (∞.5)8 |
t01(∞,8,5) 5.∞.8.∞ |
t1(∞,8,5) (8.∞)5 |
h1(∞,8,5) (10.4.10.∞)5 |
t12(∞,8,5) 5.16.∞.16 |
t2(∞,8,5) (8.5)∞ |
t02(∞,8,5) 8.10.∞.10 |
h02(∞,8,5) 4.4.4.5.4.∞.4.5 |
t012(∞,8,5) 10.16.∞ |
s(∞,8,5) 3.5.3.8.3.∞ | |||||||||
 (∞ ∞ 5) |
t0(∞,∞,5) (∞.5)∞ |
t01(∞,∞,5) 5.∞.∞.∞ |
t1(∞,∞,5) ∞10 |
h1(∞,∞,5) (10.∞)10 |
t12(∞,∞,5) 5.∞.∞.∞ |
t2(∞,∞,5) (∞.5)∞ |
t02(∞,∞,5) (∞.10)2 |
h02(∞,∞,5) (4.∞.4.5)2 |
t012(∞,∞,5) 10.∞.∞ |
s(∞,∞,5) 3.5.3.∞.3.∞ | |||||||||
 (∞ 6 6) |
t0(∞,6,6) (∞.6)6 |
h0(∞,6,6) (12.∞.12.3)6 |
t01(∞,6,6) (6.∞)2 |
h01(∞,6,6) (4.3.4.∞)2 |
t1(∞,6,6) (6.∞)6 |
h1(∞,6,6) (12.3.12.∞)6 |
t12(∞,6,6) 6.12.∞.12 |
h12(∞,6,6) 4.3.4.6.4.∞.4.6 |
t2(∞,6,6) 6∞ |
h2(∞,6,6) (∞.3)∞ |
t02(∞,6,6) 6.12.∞.12 |
h02(∞,6,6) 4.3.4.6.4.∞.4.6 |
t012(∞,6,6) 12.12.∞ |
s(∞,6,6) 3.6.3.6.3.∞ | |||||
 (∞ 7 6) |
t0(∞,7,6) (∞.6)7 |
h0(∞,7,6) (14.∞.14.3)7 |
t01(∞,7,6) 6.∞.7.∞ |
t1(∞,7,6) (7.∞)6 |
t12(∞,7,6) 6.14.∞.14 |
h12(∞,7,6) 4.3.4.7.4.∞.4.7 |
t2(∞,7,6) (7.6)∞ |
t02(∞,7,6) 7.12.∞.12 |
t012(∞,7,6) 12.14.∞ |
s(∞,7,6) 3.6.3.7.3.∞ | |||||||||
 (∞ 8 6) |
t0(∞,8,6) (∞.6)8 |
h0(∞,8,6) (16.∞.16.3)8 |
t01(∞,8,6) 6.∞.8.∞ |
h01(∞,8,6) 4.3.4.∞.4.4.4.∞ |
t1(∞,8,6) (8.∞)6 |
h1(∞,8,6) (12.4.12.∞)6 |
t12(∞,8,6) 6.16.∞.16 |
h12(∞,8,6) 4.3.4.8.4.∞.4.8 |
t2(∞,8,6) (8.6)∞ |
h2(∞,8,6) (∞.4.∞.3)∞ |
t02(∞,8,6) 8.12.∞.12 |
h02(∞,8,6) 4.4.4.6.4.∞.4.6 |
t012(∞,8,6) 12.16.∞ |
s(∞,8,6) 3.6.3.8.3.∞ | |||||
 (∞ ∞ 6) |
t0(∞,∞,6) (∞.6)∞ |
h0(∞,∞,6) (∞.∞.∞.3)∞ |
t01(∞,∞,6) 6.∞.∞.∞ |
h01(∞,∞,6) 4.3.4.∞.4.∞.4.∞ |
t1(∞,∞,6) ∞12 |
h1(∞,∞,6) (12.∞)12 |
t12(∞,∞,6) 6.∞.∞.∞ |
h12(∞,∞,6) 4.3.4.∞.4.∞.4.∞ |
t2(∞,∞,6) (∞.6)∞ |
h2(∞,∞,6) (∞.∞.∞.3)∞ |
t02(∞,∞,6) (∞.12)2 |
h02(∞,∞,6) (4.∞.4.6)2 |
t012(∞,∞,6) 12.∞.∞ |
s(∞,∞,6) 3.6.3.∞.3.∞ | |||||
 (∞ 7 7) |
t0(∞,7,7) (∞.7)7 |
t01(∞,7,7) (7.∞)2 |
t1(∞,7,7) (7.∞)7 |
t12(∞,7,7) 7.14.∞.14 |
t2(∞,7,7) 7∞ |
t02(∞,7,7) 7.14.∞.14 |
t012(∞,7,7) 14.14.∞ |
s(∞,7,7) 3.7.3.7.3.∞ | |||||||||||
 (∞ 8 7) |
t0(∞,8,7) (∞.7)8 |
t01(∞,8,7) 7.∞.8.∞ |
t1(∞,8,7) (8.∞)7 |
h1(∞,8,7) (14.4.14.∞)7 |
t12(∞,8,7) 7.16.∞.16 |
t2(∞,8,7) (8.7)∞ |
t02(∞,8,7) 8.14.∞.14 |
h02(∞,8,7) 4.4.4.7.4.∞.4.7 |
t012(∞,8,7) 14.16.∞ |
s(∞,8,7) 3.7.3.8.3.∞ | |||||||||
 (∞ ∞ 7) |
t0(∞,∞,7) (∞.7)∞ |
t01(∞,∞,7) 7.∞.∞.∞ |
t1(∞,∞,7) ∞14 |
h1(∞,∞,7) (14.∞)14 |
t12(∞,∞,7) 7.∞.∞.∞ |
t2(∞,∞,7) (∞.7)∞ |
t02(∞,∞,7) (∞.14)2 |
h02(∞,∞,7) (4.∞.4.7)2 |
t012(∞,∞,7) 14.∞.∞ |
s(∞,∞,7) 3.7.3.∞.3.∞ | |||||||||
 (∞ 8 8) |
t0(∞,8,8) (∞.8)8 |
h0(∞,8,8) (16.∞.16.4)8 |
t01(∞,8,8) (8.∞)2 |
h01(∞,8,8) (4.4.4.∞)2 |
t1(∞,8,8) (8.∞)8 |
h1(∞,8,8) (16.4.16.∞)8 |
t12(∞,8,8) 8.16.∞.16 |
h12(∞,8,8) 4.4.4.8.4.∞.4.8 |
t2(∞,8,8) 8∞ |
h2(∞,8,8) (∞.4)∞ |
t02(∞,8,8) 8.16.∞.16 |
h02(∞,8,8) 4.4.4.8.4.∞.4.8 |
t012(∞,8,8) 16.16.∞ |
s(∞,8,8) 3.8.3.8.3.∞ | |||||
 (∞ ∞ 8) |
t0(∞,∞,8) (∞.8)∞ |
h0(∞,∞,8) (∞.∞.∞.4)∞ |
t01(∞,∞,8) 8.∞.∞.∞ |
h01(∞,∞,8) 4.4.4.∞.4.∞.4.∞ |
t1(∞,∞,8) ∞16 |
h1(∞,∞,8) (16.∞)16 |
t12(∞,∞,8) 8.∞.∞.∞ |
h12(∞,∞,8) 4.4.4.∞.4.∞.4.∞ |
t2(∞,∞,8) (∞.8)∞ |
h2(∞,∞,8) (∞.∞.∞.4)∞ |
t02(∞,∞,8) (∞.16)2 |
h02(∞,∞,8) (4.∞.4.8)2 |
t012(∞,∞,8) 16.∞.∞ |
s(∞,∞,8) 3.8.3.∞.3.∞ | |||||
(∞ ∞ ∞) |
t0(∞,∞,∞) ∞∞ |
h0(∞,∞,∞) (∞.∞)∞ |
t01(∞,∞,∞) (∞.∞)2 |
h01(∞,∞,∞) (4.∞.4.∞)2 |
t1(∞,∞,∞) ∞∞ |
h1(∞,∞,∞) (∞.∞)∞ |
t12(∞,∞,∞) (∞.∞)2 |
h12(∞,∞,∞) (4.∞.4.∞)2 |
t2(∞,∞,∞) ∞∞ |
h2(∞,∞,∞) (∞.∞)∞ |
t02(∞,∞,∞) (∞.∞)2 |
h02(∞,∞,∞) (4.∞.4.∞)2 |
t012(∞,∞,∞) ∞3 |
s(∞,∞,∞) (3.∞)3 | |||||
References
[edit]- John H. Conway, Heidi Burgiel, Chaim Goodman-Strauss, The Symmetries of Things 2008, ISBN 978-1-56881-220-5 (Chapter 19, The Hyperbolic Archimedean Tessellations)
External links
[edit]- Hatch, Don. "Hyperbolic Planar Tessellations". Retrieved 2010-08-19.
- Eppstein, David. "The Geometry Junkyard: Hyperbolic Tiling". Retrieved 2010-08-19.
- Joyce, David. "Hyperbolic Tessellations". Retrieved 2010-08-19.
- Klitzing, Richard. "2D Tesselations Hyperbolic Tesselations".
- The EPINET project explores 2D hyperbolic (H²) tilings
