Kaniadakis statistics

Kaniadakis statistics (also known as κ-statistics) is a generalization of Boltzmann–Gibbs statistical mechanics, based on a relativistic generalization of the classical Boltzmann–Gibbs–Shannon entropy (commonly referred to as Kaniadakis entropy or κ-entropy). Introduced by the Greek Italian physicist Giorgio Kaniadakis in 2001, κ-statistical mechanics preserve the main features of ordinary statistical mechanics and have attracted the interest of many researchers in recent years. The κ-distribution is currently considered one of the most viable candidates for explaining complex physical, natural or artificial systems involving power-law tailed statistical distributions. Kaniadakis statistics have been adopted successfully in the description of a variety of systems in the fields of cosmology, astrophysics, condensed matter, quantum physics, seismology, genomics, economics, epidemiology, and many others.

Mathematical formalism

The mathematical formalism of κ-statistics is generated by κ-deformed functions, especially the κ-exponential function.

κ-exponential function

Plot of the κ-exponential function $\exp _{\kappa }(x)$ for three different κ-values. The solid black curve corresponding to the ordinary exponential function $\exp(x)$ ($\kappa =0$).

The Kaniadakis exponential (or κ-exponential) function is a one-parameter generalization of an exponential function, given by:

$\exp _{\kappa }(x)={\begin{cases}{\Big (}{\sqrt {1+\kappa ^{2}x^{2}}}+\kappa x{\Big )}^{\frac {1}{\kappa }}&{\text{if }}0<\kappa <1.\\[6pt]\exp(x)&{\text{if }}\kappa =0,\\[8pt]\end{cases}}$

with $\exp _{-\kappa }(x)=\exp _{\kappa }(x)$.

The κ-exponential for $0<\kappa <1$ can also be written in the form:

$\exp _{\kappa }(x)=\exp {\Bigg (}{\frac {1}{\kappa }}{\text{arcsinh}}(\kappa x){\Bigg )}.$

The first five terms of the Taylor expansion of $\exp _{\kappa }(x)$ are given by:

$\exp _{\kappa }(x)=1+x+{\frac {x^{2}}{2}}+(1-\kappa ^{2}){\frac {x^{3}}{3!}}+(1-4\kappa ^{2}){\frac {x^{4}}{4!}}+\cdots$

where the first three are the same as a typical exponential function.

Basic properties

The κ-exponential function has the following properties of an exponential function:

$\exp _{\kappa }(x)\in \mathbb {C} ^{\infty }(\mathbb {R} )$

${\frac {d}{dx}}\exp _{\kappa }(x)>0$

${\frac {d^{2}}{dx^{2}}}\exp _{\kappa }(x)>0$

$\exp _{\kappa }(-\infty )=0^{+}$

$\exp _{\kappa }(0)=1$

$\exp _{\kappa }(+\infty )=+\infty$

$\exp _{\kappa }(x)\exp _{\kappa }(-x)=-1$

For a real number $r$, the κ-exponential has the property:

${\Big [}\exp _{\kappa }(x){\Big ]}^{r}=\exp _{\kappa /r}(rx)$.

κ-logarithm function

Plot of the κ-logarithmic function $\ln _{\kappa }(x)$ for three different κ-values. The solid black curve corresponding to the ordinary logarithmic function $\ln(x)$ ($\kappa =0$).

The Kaniadakis logarithm (or κ-logarithm) is a relativistic one-parameter generalization of the ordinary logarithm function,

$\ln _{\kappa }(x)={\begin{cases}{\frac {x^{\kappa }-x^{-\kappa }}{2\kappa }}&{\text{if }}0<\kappa <1,\\[8pt]\ln(x)&{\text{if }}\kappa =0,\\[8pt]\end{cases}}$

with $\ln _{-\kappa }(x)=\ln _{\kappa }(x)$, which is the inverse function of the κ-exponential:

$\ln _{\kappa }{\Big (}\exp _{\kappa }(x){\Big )}=\exp _{\kappa }{\Big (}\ln _{\kappa }(x){\Big )}=x.$

The κ-logarithm for $0<\kappa <1$ can also be written in the form:

$\ln _{\kappa }(x)={\frac {1}{\kappa }}\sinh {\Big (}\kappa \ln(x){\Big )}$

The first three terms of the Taylor expansion of $\ln _{\kappa }(x)$ are given by:

$\ln _{\kappa }(1+x)=x-{\frac {x^{2}}{2}}+\left(1+{\frac {\kappa ^{2}}{2}}\right){\frac {x^{3}}{3}}-\cdots$

following the rule

$\ln _{\kappa }(1+x)=\sum _{n=1}^{\infty }b_{n}(\kappa )\,(-1)^{n-1}\,{\frac {x^{n}}{n}}$

with $b_{1}(\kappa )=1$, and

$b_{n}(\kappa )(x)={\begin{cases}1&{\text{if }}n=1,\\[8pt]{\frac {1}{2}}{\Big (}1-\kappa {\Big )}{\Big (}1-{\frac {\kappa }{2}}{\Big )}...{\Big (}1-{\frac {\kappa }{n-1}}{\Big )},\,+\,{\frac {1}{2}}{\Big (}1+\kappa {\Big )}{\Big (}1+{\frac {\kappa }{2}}{\Big )}...{\Big (}1+{\frac {\kappa }{n-1}}{\Big )}&{\text{for }}n>1,\\[8pt]\end{cases}}$

where $b_{n}(0)=1$ and $b_{n}(-\kappa )=b_{n}(\kappa )$. The two first terms of the Taylor expansion of $\ln _{\kappa }(x)$ are the same as an ordinary logarithmic function.

Basic properties

The κ-logarithm function has the following properties of a logarithmic function:

$\ln _{\kappa }(x)\in \mathbb {C} ^{\infty }(\mathbb {R} ^{+})$

${\frac {d}{dx}}\ln _{\kappa }(x)>0$

${\frac {d^{2}}{dx^{2}}}\ln _{\kappa }(x)<0$

$\ln _{\kappa }(0^{+})=-\infty$

$\ln _{\kappa }(1)=0$

$\ln _{\kappa }(+\infty )=+\infty$

$\ln _{\kappa }(1/x)=-\ln _{\kappa }(x)$

For a real number $r$, the κ-logarithm has the property:

$\ln _{\kappa }(x^{r})=r\ln _{r\kappa }(x)$

κ-Algebra

κ-sum

For any $x,y\in \mathbb {R}$ and $|\kappa |<1$, the Kaniadakis sum (or κ-sum) is defined by the following composition law:

$x{\stackrel {\kappa }{\oplus }}y=x{\sqrt {1+\kappa ^{2}y^{2}}}+y{\sqrt {1+\kappa ^{2}x^{2}}}$,

that can also be written in form:

$x{\stackrel {\kappa }{\oplus }}y={1 \over \kappa }\,\sinh \left({\rm {arcsinh}}\,(\kappa x)\,+\,{\rm {arcsinh}}\,(\kappa y)\,\right)$,

where the ordinary sum is a particular case in the classical limit $\kappa \rightarrow 0$: $x{\stackrel {0}{\oplus }}y=x+y$.

The κ-sum, like the ordinary sum, has the following properties:

${\text{1. associativity:}}\quad (x{\stackrel {\kappa }{\oplus }}y){\stackrel {\kappa }{\oplus }}z=x{\stackrel {\kappa }{\oplus }}(y{\stackrel {\kappa }{\oplus }}z)$

${\text{2. neutral element:}}\quad x{\stackrel {\kappa }{\oplus }}0=0{\stackrel {\kappa }{\oplus }}x=x$

${\text{3. opposite element:}}\quad x{\stackrel {\kappa }{\oplus }}(-x)=(-x){\stackrel {\kappa }{\oplus }}x=0$

${\text{4. commutativity:}}\quad x{\stackrel {\kappa }{\oplus }}y=y{\stackrel {\kappa }{\oplus }}x$

The κ-difference ${\stackrel {\kappa }{\ominus }}$ is given by $x{\stackrel {\kappa }{\ominus }}y=x{\stackrel {\kappa }{\oplus }}(-y)$.

The fundamental property $\exp _{\kappa }(-x)\exp _{\kappa }(x)=1$ arises as a special case of the more general expression below: $\exp _{\kappa }(x)\exp _{\kappa }(y)=exp_{\kappa }(x{\stackrel {\kappa }{\oplus }}y)$

Furthermore, the κ-functions and the κ-sum present the following relationships:

$\ln _{\kappa }(x\,y)=\ln _{\kappa }(x){\stackrel {\kappa }{\oplus }}\ln _{\kappa }(y)$

κ-product

For any $x,y\in \mathbb {R}$ and $|\kappa |<1$, the Kaniadakis product (or κ-product) is defined by the following composition law:

$x{\stackrel {\kappa }{\otimes }}y={1 \over \kappa }\,\sinh \left(\,{1 \over \kappa }\,\,{\rm {arcsinh}}\,(\kappa x)\,\,{\rm {arcsinh}}\,(\kappa y)\,\right)$,

where the ordinary product is a particular case in the classical limit $\kappa \rightarrow 0$: $x{\stackrel {0}{\otimes }}y=x\times y=xy$.

The κ-product, like the ordinary product, has the following properties:

${\text{1. associativity:}}\quad (x{\stackrel {\kappa }{\otimes }}y){\stackrel {\kappa }{\otimes }}z=x{\stackrel {\kappa }{\otimes }}(y{\stackrel {\kappa }{\otimes }}z)$

${\text{2. neutral element:}}\quad x{\stackrel {\kappa }{\otimes }}I=I{\stackrel {\kappa }{\otimes }}x=x\quad {\text{for}}\quad I=\kappa ^{-1}\sinh \kappa {\stackrel {\kappa }{\oplus }}x=x$

${\text{3. inverse element:}}\quad x{\stackrel {\kappa }{\otimes }}{\overline {x}}={\overline {x}}{\stackrel {\kappa }{\otimes }}x=I\quad {\text{for}}\quad {\overline {x}}=\kappa ^{-1}\sinh(\kappa ^{2}/{\rm {arcsinh}}\,(\kappa x))$

${\text{4. commutativity:}}\quad x{\stackrel {\kappa }{\otimes }}y=y{\stackrel {\kappa }{\otimes }}x$

The κ-division ${\stackrel {\kappa }{\oslash }}$ is given by $x{\stackrel {\kappa }{\oslash }}y=x{\stackrel {\kappa }{\otimes }}{\overline {y}}$.

The κ-sum ${\stackrel {\kappa }{\oplus }}$ and the κ-product ${\stackrel {\kappa }{\otimes }}$ obey the distributive law: $z{\stackrel {\kappa }{\otimes }}(x{\stackrel {\kappa }{\oplus }}y)=(z{\stackrel {\kappa }{\otimes }}x){\stackrel {\kappa }{\oplus }}(z{\stackrel {\kappa }{\otimes }}y)$.

The fundamental property $\ln _{\kappa }(1/x)=-\ln _{\kappa }(x)$ arises as a special case of the more general expression below:

$\ln _{\kappa }(x\,y)=\ln _{\kappa }(x){\stackrel {\kappa }{\oplus }}\ln _{\kappa }(y)$

Furthermore, the κ-functions and the κ-product present the following relationships:

$\exp _{\kappa }(x){\stackrel {\kappa }{\otimes }}\exp _{\kappa }(y)=\exp _{\kappa }(x\,+\,y)$

$\ln _{\kappa }(x\,{\stackrel {\kappa }{\otimes }}\,y)=\ln _{\kappa }(x)+\ln _{\kappa }(y)$

κ-Calculus

κ-Differential

The Kaniadakis differential (or κ-differential) of $x$ is defined by:

$\mathrm {d} _{\kappa }x={\frac {\mathrm {d} \,x}{\displaystyle {\sqrt {1+\kappa ^{2}\,x^{2}}}}}$.

So, the κ-derivative of a function $f(x)$ is related to the Leibniz derivative through:

${\frac {\mathrm {d} f(x)}{\mathrm {d} _{\kappa }x}}=\gamma _{\kappa }(x){\frac {\mathrm {d} f(x)}{\mathrm {d} x}}$,

where $\gamma _{\kappa }(x)={\sqrt {1+\kappa ^{2}x^{2}}}$ is the Lorentz factor. The ordinary derivative ${\frac {\mathrm {d} f(x)}{\mathrm {d} x}}$ is a particular case of κ-derivative ${\frac {\mathrm {d} f(x)}{\mathrm {d} _{\kappa }x}}$ in the classical limit $\kappa \rightarrow 0$.

κ-Integral

The Kaniadakis integral (or κ-integral) is the inverse operator of the κ-derivative defined through

$\int \mathrm {d} _{\kappa }x\,\,f(x)=\int {\frac {\mathrm {d} \,x}{\sqrt {1+\kappa ^{2}\,x^{2}}}}\,\,f(x)$,

which recovers the ordinary integral in the classical limit $\kappa \rightarrow 0$.

κ-Trigonometry

κ-Cyclic Trigonometry

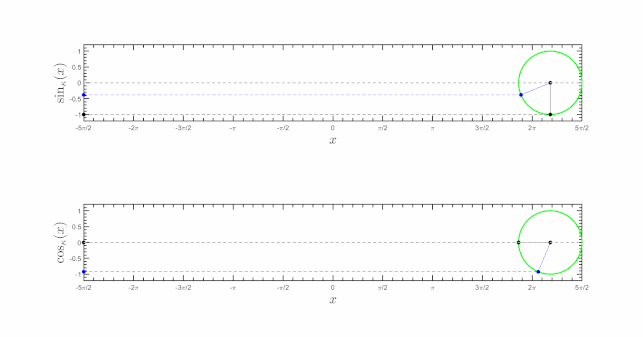
[click on the figure] Plot of the κ-sine and κ-cosine functions for $\kappa =0$ (black curve) and $\kappa =0.1$ (blue curve).

The Kaniadakis cyclic trigonometry (or κ-cyclic trigonometry) is based on the κ-cyclic sine (or κ-sine) and κ-cyclic cosine (or κ-cosine) functions defined by:

$\sin _{\kappa }(x)={\frac {\exp _{\kappa }(ix)-\exp _{\kappa }(-ix)}{2i}}$,

$\cos _{\kappa }(x)={\frac {\exp _{\kappa }(ix)+\exp _{\kappa }(-ix)}{2}}$,

where the κ-generalized Euler formula is

$\exp _{\kappa }(\pm ix)=\cos _{\kappa }(x)\pm i\sin _{\kappa }(x)$.:

The κ-cyclic trigonometry preserves fundamental expressions of the ordinary cyclic trigonometry, which is a special case in the limit κ → 0, such as:

$\cos _{\kappa }^{2}(x)+\sin _{\kappa }^{2}(x)=1$

$\sin _{\kappa }(x{\stackrel {\kappa }{\oplus }}y)=\sin _{\kappa }(x)\cos _{\kappa }(y)+\cos _{\kappa }(x)\sin _{\kappa }(y)$.

The κ-cyclic tangent and κ-cyclic cotangent functions are given by:

$\tan _{\kappa }(x)={\frac {\sin _{\kappa }(x)}{\cos _{\kappa }(x)}}$

$\cot _{\kappa }(x)={\frac {\cos _{\kappa }(x)}{\sin _{\kappa }(x)}}$.

The κ-cyclic trigonometric functions become the ordinary trigonometric function in the classical limit $\kappa \rightarrow 0$.

κ-Inverse cyclic function

The Kaniadakis inverse cyclic functions (or κ-inverse cyclic functions) are associated to the κ-logarithm:

${\rm {arcsin}}_{\kappa }(x)=-i\ln _{\kappa }\left({\sqrt {1-x^{2}}}+ix\right)$,

${\rm {arccos}}_{\kappa }(x)=-i\ln _{\kappa }\left({\sqrt {x^{2}-1}}+x\right)$,

${\rm {arctan}}_{\kappa }(x)=i\ln _{\kappa }\left({\sqrt {\frac {1-ix}{1+ix}}}\right)$,

${\rm {arccot}}_{\kappa }(x)=i\ln _{\kappa }\left({\sqrt {\frac {ix+1}{ix-1}}}\right)$.

κ-Hyperbolic Trigonometry

The Kaniadakis hyperbolic trigonometry (or κ-hyperbolic trigonometry) is based on the κ-hyperbolic sine and κ-hyperbolic cosine given by:

$\sinh _{\kappa }(x)={\frac {\exp _{\kappa }(x)-\exp _{\kappa }(-x)}{2}}$,

$\cosh _{\kappa }(x)={\frac {\exp _{\kappa }(x)+\exp _{\kappa }(-x)}{2}}$,

where the κ-Euler formula is

$\exp _{\kappa }(\pm x)=\cosh _{\kappa }(x)\pm \sinh _{\kappa }(x)$.

The κ-hyperbolic tangent and κ-hyperbolic cotangent functions are given by:

$\tanh _{\kappa }(x)={\frac {\sinh _{\kappa }(x)}{\cosh _{\kappa }(x)}}$

$\coth _{\kappa }(x)={\frac {\cosh _{\kappa }(x)}{\sinh _{\kappa }(x)}}$.

The κ-hyperbolic trigonometric functions become the ordinary hyperbolic trigonometric functions in the classical limit $\kappa \rightarrow 0$.

From the κ-Euler formula and the property $\exp _{\kappa }(-x)\exp _{\kappa }(x)=1$ the fundamental expression of κ-hyperbolic trigonometry is given as follows:

$\cosh _{\kappa }^{2}(x)-\sinh _{\kappa }^{2}(x)=1$

κ-Inverse hyperbolic function

The Kaniadakis inverse hyperbolic functions (or κ-inverse hyperbolic functions) are associated to the κ-logarithm:

${\rm {arcsinh}}_{\kappa }(x)=\ln _{\kappa }\left({\sqrt {1+x^{2}}}+x\right)$,

${\rm {arccosh}}_{\kappa }(x)=\ln _{\kappa }\left({\sqrt {x^{2}-1}}+x\right)$,

${\rm {arctanh}}_{\kappa }(x)=\ln _{\kappa }\left({\sqrt {\frac {1+x}{1-x}}}\right)$,

${\rm {arccoth}}_{\kappa }(x)=\ln _{\kappa }\left({\sqrt {\frac {1-x}{1+x}}}\right)$,

in which are valid the following relations:

${\rm {arcsinh}}_{\kappa }(x)={\rm {sign}}(x){\rm {arccosh}}_{\kappa }\left({\sqrt {1+x^{2}}}\right)$,

${\rm {arcsinh}}_{\kappa }(x)={\rm {arctanh}}_{\kappa }\left({\frac {x}{\sqrt {1+x^{2}}}}\right)$,

${\rm {arcsinh}}_{\kappa }(x)={\rm {arccoth}}_{\kappa }\left({\frac {\sqrt {1+x^{2}}}{x}}\right)$.

The κ-cyclic and κ-hyperbolic trigonometric functions are connected by the following relationships:

${\rm {sin}}_{\kappa }(x)=-i{\rm {sinh}}_{\kappa }(ix)$,

${\rm {cos}}_{\kappa }(x)={\rm {cosh}}_{\kappa }(ix)$,

${\rm {tan}}_{\kappa }(x)=-i{\rm {tanh}}_{\kappa }(ix)$,

${\rm {cot}}_{\kappa }(x)=i{\rm {coth}}_{\kappa }(ix)$,

${\rm {arcsin}}_{\kappa }(x)=-i\,{\rm {arcsinh}}_{\kappa }(ix)$,

${\rm {arccos}}_{\kappa }(x)\neq -i\,{\rm {arccosh}}_{\kappa }(ix)$,

${\rm {arctan}}_{\kappa }(x)=-i\,{\rm {arctanh}}_{\kappa }(ix)$,

${\rm {arccot}}_{\kappa }(x)=i\,{\rm {arccoth}}_{\kappa }(ix)$.

Kaniadakis entropy

The Kaniadakis statistics is based on the Kaniadakis κ-entropy, which is defined through:

$S_{\kappa }{\big (}p{\big )}=-\sum _{i}p_{i}\ln _{\kappa }{\big (}p_{i}{\big )}=\sum _{i}p_{i}\ln _{\kappa }{\bigg (}{\frac {1}{p_{i}}}{\bigg )}$

where $p=\{p_{i}=p(x_{i});x\in \mathbb {R} ;i=1,2,...,N;\sum _{i}p_{i}=1\}$ is a probability distribution function defined for a random variable $X$, and $0\leq |\kappa |<1$ is the entropic index.

The Kaniadakis κ-entropy is thermodynamically and Lesche stable and obeys the Shannon-Khinchin axioms of continuity, maximality, generalized additivity and expandability.

Kaniadakis distributions

Main article: Kaniadakis distribution

A Kaniadakis distribution (or κ-distribution) is a probability distribution derived from the maximization of Kaniadakis entropy under appropriate constraints. In this regard, several probability distributions emerge for analyzing a wide variety of phenomenology associated with experimental power-law tailed statistical distributions.

κ-Exponential distribution

Main article: Kaniadakis Exponential distribution

κ-Gaussian distribution

Main article: Kaniadakis Gaussian distribution

κ-Gamma distribution

Main article: Kaniadakis Gamma distribution

κ-Weibull distribution

Main article: Kaniadakis Weibull distribution

κ-Logistic distribution

Main article: Kaniadakis Logistic distribution

Kaniadakis integral transform

κ-Laplace Transform

The Kaniadakis Laplace transform (or κ-Laplace transform) is a κ-deformed integral transform of the ordinary Laplace transform. The κ-Laplace transform converts a function $f$ of a real variable $t$ to a new function $F_{\kappa }(s)$ in the complex frequency domain, represented by the complex variable $s$. This κ-integral transform is defined as:

$F_{\kappa }(s)={\cal {L}}_{\kappa }\{f(t)\}(s)=\int _{\,0}^{\infty }\!f(t)\,[\exp _{\kappa }(-t)]^{s}\,dt$

The inverse κ-Laplace transform is given by:

$f(t)={\cal {L}}_{\kappa }^{-1}\{F_{\kappa }(s)\}(t)={{\frac {1}{2\pi i}}\int _{c-i\infty }^{c+i\infty }\!F_{\kappa }(s)\,{\frac {[\exp _{\kappa }(t)]^{s}}{\sqrt {1+\kappa ^{2}t^{2}}}}\,ds}$

The ordinary Laplace transform and its inverse transform are recovered as $\kappa \rightarrow 0$.

Properties

Let two functions $f(t)={\cal {L}}_{\kappa }^{-1}\{F_{\kappa }(s)\}(t)$ and $g(t)={\cal {L}}_{\kappa }^{-1}\{G_{\kappa }(s)\}(t)$, and their respective κ-Laplace transforms $F_{\kappa }(s)$ and $G_{\kappa }(s)$, the following table presents the main properties of κ-Laplace transform:

Properties of the κ-Laplace transform

Property	$f(t)$	$F_{\kappa }(s)$
Linearity	$a\,f(t)+b\,g(t)$	$a\,F_{\kappa }(s)+b\,G_{\kappa }(s)$
Time scaling	$f(at)$	${\frac {1}{a}}\,F_{\kappa /a}({\frac {s}{a}})$
Frequency shifting	$f(t)\,[\exp _{\kappa }(-t)]^{a}$	$F_{\kappa }(s-a)$
Derivative	${\frac {d\,f(t)}{dt}}$	$s\,{\cal {L}}_{\kappa }\left\{{\frac {f(t)}{\sqrt {1+\kappa ^{2}t^{2}}}}\right\}(s)-f(0)$
Derivative	${\frac {d}{dt}}\,{\sqrt {1+\kappa ^{2}t^{2}}}\,f(t)$	$s\,F_{\kappa }(s)-f(0)$
Time-domain integration	${\frac {1}{\sqrt {1+\kappa ^{2}t^{2}}}}\,\int _{0}^{t}f(w)dw$	${\frac {1}{s}}\,F_{\kappa }(s)$
	$f(t)\,[\ln(\exp _{\kappa }(t))]^{n}$	$(-1)^{n}{\frac {d^{n}F_{\kappa }(s)}{ds^{n}}}$
	$f(t)\,[\ln(\exp _{\kappa }(t))]^{-n}$	$\int _{s}^{+\infty }dw_{n}\int _{w_{n}}^{+\infty }dw_{n-1}...\int _{w_{3}}^{+\infty }dw_{2}\int _{w_{2}}^{+\infty }dw_{1}\,F_{\kappa }(w_{1})$
Dirac delta-function	$\delta (t-\tau )$	$[\exp _{\kappa }(-\tau )]^{s}$
Heaviside unit function	$u(t-\tau )$	${\frac {s{\sqrt {1+\kappa ^{2}\tau ^{2}}}+\kappa ^{2}\tau }{s^{2}-\kappa ^{2}}}\,[\exp _{\kappa }(-\tau )]^{s}$
Power function	$t^{\nu -1}$	${\frac {s^{2}}{s^{2}-\kappa ^{2}\nu ^{2}}}\,{\frac {\Gamma _{\frac {\kappa }{s}}(\nu +1)}{\nu \,s^{\nu }}}={\frac {s}{s+|\kappa |\nu }}\,{\frac {\Gamma (\nu )}{|2\kappa |^{\nu }}}\,{\frac {\Gamma \left({\frac {s}{|2\kappa |}}-{\frac {\nu }{2}}\right)}{\Gamma \left({\frac {s}{|2\kappa |}}+{\frac {\nu }{2}}\right)}}$
Power function	$t^{2m-1},\ \ m\in Z^{+}$	${\frac {(2m-1)!}{\prod _{j=1}^{m}\left[s^{2}-(2j)^{2}\kappa ^{2}\right]}}$
Power function	$t^{2m},\ \ m\in Z^{+}$	${\frac {(2m)!\,s}{\prod _{j=1}^{m+1}\left[s^{2}-(2j-1)^{2}\kappa ^{2}\right]}}$

The κ-Laplace transforms presented in the latter table reduce to the corresponding ordinary Laplace transforms in the classical limit $\kappa \rightarrow 0$.

κ-Fourier Transform

The Kaniadakis Fourier transform (or κ-Fourier transform) is a κ-deformed integral transform of the ordinary Fourier transform, which is consistent with the κ-algebra and the κ-calculus. The κ-Fourier transform is defined as:

${\cal {F}}_{\kappa }[f(x)](\omega )={1 \over {\sqrt {2\,\pi }}}\int \limits _{-\infty }\limits ^{+\infty }f(x)\,\exp _{\kappa }(-x\otimes _{\kappa }\omega )^{i}\,d_{\kappa }x$

which can be rewritten as

${\cal {F}}_{\kappa }[f(x)](\omega )={1 \over {\sqrt {2\,\pi }}}\int \limits _{-\infty }\limits ^{+\infty }f(x)\,{\exp(-i\,x_{\{\kappa \}}\,\omega _{\{\kappa \}}) \over {\sqrt {1+\kappa ^{2}\,x^{2}}}}\,dx$

where $x_{\{\kappa \}}={\frac {1}{\kappa }}\,{\rm {arcsinh}}\,(\kappa \,x)$ and $\omega _{\{\kappa \}}={\frac {1}{\kappa }}\,{\rm {arcsinh}}\,(\kappa \,\omega )$. The κ-Fourier transform imposes an asymptotically log-periodic behavior by deforming the parameters $x$ and $\omega$ in addition to a damping factor, namely ${\sqrt {1+\kappa ^{2}\,x^{2}}}$.

Real (top panel) and imaginary (bottom panel) part of the kernel $h_{\kappa }(x,\omega )$ for typical $\kappa$-values and $\omega =1$.

The kernel of the κ-Fourier transform is given by:

$h_{\kappa }(x,\omega )={\frac {\exp(-i\,x_{\{\kappa \}}\,\omega _{\{\kappa \}})}{\sqrt {1+\kappa ^{2}\,x^{2}}}}$

The inverse κ-Fourier transform is defined as:

${\cal {F}}_{\kappa }[{\hat {f}}(\omega )](x)={1 \over {\sqrt {2\,\pi }}}\int \limits _{-\infty }\limits ^{+\infty }{\hat {f}}(\omega )\,\exp _{\kappa }(\omega \otimes _{\kappa }x)^{i}\,d_{\kappa }\omega$

Let $u_{\kappa }(x)={\frac {1}{\kappa }}\cosh {\Big (}\kappa \ln(x){\Big )}$, the following table shows the κ-Fourier transforms of several notable functions:

κ-Fourier transform of several functions

	$f(x)$	${\cal {F}}_{\kappa }[f(x)](\omega )$
Step function	$\theta (x)$	${\sqrt {2\,\pi }}\,\delta (\omega )+{1 \over {\sqrt {2\,\pi }}\,i\,\omega _{\{\kappa \}}}$
Modulation	$\cos _{\kappa }(a{\stackrel {\kappa }{\oplus }}x)$	${\sqrt {\pi \over 2}}\,u_{\kappa }(\exp _{\kappa }(a))\,\left(\delta (\omega +a)+\delta (\omega -a)\right)$
Causal $\kappa$-exponential	$\theta (x)\,\exp _{\kappa }(-a{\stackrel {\kappa }{\otimes }}x)$	${1 \over {\sqrt {2\,\pi }}}{1 \over a_{\{\kappa \}}+i\,\omega _{\{\kappa \}}}$
Symmetric $\kappa$-exponential	$\exp _{\kappa }(-a{\stackrel {\kappa }{\otimes }}|x|)$	${\sqrt {2 \over \pi }}\,{a_{\{\kappa \}} \over a_{\{\kappa \}}^{2}+\omega _{\{\kappa \}}^{2}}$
Constant	$1$	${\sqrt {2\,\pi }}\,\delta (\omega )$
$\kappa$-Phasor	$\exp _{\kappa }\,(a{\stackrel {\kappa }{\otimes }}x)^{i}$	${\sqrt {2\,\pi }}\,u_{\kappa }(\exp _{\kappa }(a))\,\delta (\omega -a)$
Impuslse	$\delta (x-a)$	${1 \over {\sqrt {2\,\pi }}}{\exp _{\kappa }\,(\omega {\stackrel {\kappa }{\otimes }}a)^{i} \over u_{\kappa }\left(\exp _{\kappa }\,(a)\right)}$
Signum	Sgn$(x)$	${\sqrt {2 \over \pi }}\,\,{1 \over i\,\omega _{\{\kappa \}}}$
Rectangular	$\Pi \left({x \over a}\right)$	${\sqrt {2 \over \pi }}\,\,a_{\{\kappa \}}\,{\rm {sinc}}_{\kappa }(\omega {\stackrel {\kappa }{\otimes }}a)$

The κ-deformed version of the Fourier transform preserves the main properties of the ordinary Fourier transform, as summarized in the following table.

κ-Fourier properties

$f(x)$	${\cal {F}}_{\kappa }[f(x)](\omega )$
Linearity	${\cal {F}}_{\kappa }[\alpha \,f(x)+\beta \,g(x)](\omega )=\alpha \,{\cal {F}}_{\kappa }[f(x)](\omega )+\beta \,{\cal {F}}_{\kappa }[g(x)](\omega )$
Scaling	${\cal {F}}_{\kappa }\left[f(\alpha \,x)\right](\omega )={1 \over \alpha }\,{\cal {F}}_{\kappa ^{\prime }}\left[f(x)\right](\omega ^{\prime })$ where $\kappa ^{\prime }=\kappa /\alpha$ and $\omega ^{\prime }=(a/\kappa )\,\sinh \left({\rm {arcsinh}}(\kappa \,\omega )/a^{2}\right)$
$\kappa$-Scaling	${\cal {F}}_{\kappa }\left[f(\alpha {\stackrel {\kappa }{\otimes }}x)\right](\omega )={1 \over \alpha _{\{\kappa \}}}\,{\cal {F}}_{\kappa }[f(x)]\left({\frac {1}{\alpha }}{\stackrel {\kappa }{\otimes }}\omega \right)$
Complex conjugation	${\cal {F}}_{\kappa }{\big [}f(x){\big ]}^{\ast }(\omega )={\cal {F}}_{\kappa }{\big [}f(x){\big ]}(-\omega )$
Duality	${\cal {F}}_{\kappa }{\Big [}{\cal {F}}_{\kappa }{\big [}f(x){\big ]}(\nu ){\Big ]}(\omega )=f(-\omega )$
Reverse	${\cal {F}}_{\kappa }\left[f(-x)\right](\omega )={\cal {F}}_{\kappa }[f(x)](-\omega )$
$\kappa$-Frequency shift	${\cal {F}}_{\kappa }\left[\exp _{\kappa }(\omega _{0}{\stackrel {\kappa }{\otimes }}x)^{i}f(x)\right](\omega )={\cal {F}}_{\kappa }[f(x)](\omega {\stackrel {\kappa }{\ominus }}\omega _{0})$
$\kappa$-Time shift	${\cal {F}}_{\kappa }\left[f(x\,{\stackrel {\kappa }{\oplus }}\,x_{0})\right](\omega )=\exp _{\kappa }(\omega \,{\stackrel {\kappa }{\otimes }}\,x_{0})^{i}\,{\cal {F}}_{\kappa }[f(x)](\omega )$
Transform of $\kappa$-derivative	${\cal {F}}_{\kappa }\left[{\frac {d\,f(x)}{d_{\kappa }x}}\right](\omega )=i\,\omega _{\{\kappa \}}\,{\cal {F}}_{\kappa }[f(x)](\omega )$
$\kappa$-Derivative of transform	${\frac {d}{d_{\kappa }\omega }}\,{\cal {F}}_{\kappa }[f(x)](\omega )=-i\,\omega _{\{\kappa \}}\,{\cal {F}}_{\kappa }\left[x_{\{\kappa \}}\,f(x)\right](\omega )$
Transform of integral	${\cal {F}}_{\kappa }\left[\int \limits _{-\infty }\limits ^{x}f(y)\,dy\right](\omega )={1 \over i\,\omega _{\{\kappa \}}}{\cal {F}}_{\kappa }[f(x)](\omega )+2\,\pi \,{\cal {F}}_{\kappa }[f(x)](0)\,\delta (\omega )$
$\kappa$-Convolution	${\cal {F}}_{\kappa }\left[(f\,{\stackrel {\kappa }{\circledast }}\,g)(x)\right](\omega )={\sqrt {2\,\pi }}\,{\cal {F}}_{\kappa }[f(x)](\omega )\,{\cal {F}}_{\kappa }[g(x)](\omega )$ where $(f\,{\stackrel {\kappa }{\circledast }}\,g)(x)=\int \limits _{-\infty }\limits ^{+\infty }f(y)\,g(x\,{\stackrel {\kappa }{\ominus }}\,y)\,d_{\kappa }y$
Modulation	${\cal {F}}_{\kappa }\left[f(x)\,g(x)\right](\omega )={1 \over {\sqrt {2\,\pi }}}\left({\cal {F}}_{\kappa }\left[f(x)\right]\,{\stackrel {\kappa }{\circledast }}\,{\cal {F}}_{\kappa }\left[g(x)\right]\right)(\omega )$

The properties of the κ-Fourier transform presented in the latter table reduce to the corresponding ordinary Fourier transforms in the classical limit $\kappa \rightarrow 0$.

See also

• Giorgio Kaniadakis
• Kaniadakis distribution
• Kaniadakis κ-Exponential distribution
• Kaniadakis κ-Gaussian distribution
• Kaniadakis κ-Gamma distribution
• Kaniadakis κ-Weibull distribution
• Kaniadakis κ-Logistic distribution
• Kaniadakis κ-Erlang distribution

References

•  This article incorporates text available under the CC BY 3.0 license.

External links

• Giorgio Kaniadakis Google Scholar page
• Kaniadakis Statistics on arXiv.org