Monoidal functor
In category theory, monoidal functors are functors between monoidal categories which preserve the monoidal structure. More specifically, a monoidal functor between two monoidal categories consists of a functor between the categories, along with two coherence maps—a natural transformation and a morphism that preserve monoidal multiplication and unit, respectively. Mathematicians require these coherence maps to satisfy additional properties depending on how strictly they want to preserve the monoidal structure; each of these properties gives rise to a slightly different definition of monoidal functors
- The coherence maps of lax monoidal functors satisfy no additional properties; they are not necessarily invertible.
- The coherence maps of strong monoidal functors are invertible.
- The coherence maps of strict monoidal functors are identity maps.
Although we distinguish between these different definitions here, authors may call any one of these simply monoidal functors.
Definition
[edit]Let and be monoidal categories. A lax monoidal functor from to (which may also just be called a monoidal functor) consists of a functor together with a natural transformation
between functors and a morphism
- ,
called the coherence maps or structure morphisms, which are such that for every three objects , and of the diagrams
commute in the category . Above, the various natural transformations denoted using are parts of the monoidal structure on and .[1]
Variants
[edit]- The dual of a monoidal functor is a comonoidal functor; it is a monoidal functor whose coherence maps are reversed. Comonoidal functors may also be called opmonoidal, colax monoidal, or oplax monoidal functors.
- A strong monoidal functor is a monoidal functor whose coherence maps are invertible.
- A strict monoidal functor is a monoidal functor whose coherence maps are identities.
- A braided monoidal functor is a monoidal functor between braided monoidal categories (with braidings denoted ) such that the following diagram commutes for every pair of objects A, B in :
- A symmetric monoidal functor is a braided monoidal functor whose domain and codomain are symmetric monoidal categories.
Examples
[edit]- The underlying functor from the category of abelian groups to the category of sets. In this case, the map sends (a, b) to ; the map sends to 1.
- If is a (commutative) ring, then the free functor extends to a strongly monoidal functor (and also if is commutative).
- If is a homomorphism of commutative rings, then the restriction functor is monoidal and the induction functor is strongly monoidal.
- An important example of a symmetric monoidal functor is the mathematical model of topological quantum field theory, which has been recently developed. Let be the category of cobordisms of n-1,n-dimensional manifolds with tensor product given by disjoint union, and unit the empty manifold. A topological quantum field theory in dimension n is a symmetric monoidal functor
- The homology functor is monoidal as via the map .
Alternate notions
[edit]If and are closed monoidal categories with internal hom-functors (we drop the subscripts for readability), there is an alternative formulation
- ψAB : F(A ⇒ B) → FA ⇒ FB
of φAB commonly used in functional programming. The relation between ψAB and φAB is illustrated in the following commutative diagrams:
Properties
[edit]- If is a monoid object in , then is a monoid object in .[2]
Monoidal functors and adjunctions
[edit]Suppose that a functor is left adjoint to a monoidal . Then has a comonoidal structure induced by , defined by
and
- .
If the induced structure on is strong, then the unit and counit of the adjunction are monoidal natural transformations, and the adjunction is said to be a monoidal adjunction; conversely, the left adjoint of a monoidal adjunction is always a strong monoidal functor.
Similarly, a right adjoint to a comonoidal functor is monoidal, and the right adjoint of a comonoidal adjunction is a strong monoidal functor.
See also
[edit]Inline citations
[edit]- ^ Perrone (2024), pp. 360–364
- ^ Perrone (2024), pp. 367–368
References
[edit]- Kelly, G. Max (1974). "Doctrinal adjunction". Category Seminar. Lecture Notes in Mathematics. Vol. 420. Springer. pp. 257–280. doi:10.1007/BFb0063105. ISBN 978-3-540-37270-7.
- Perrone, Paolo (2024). Starting Category Theory. World Scientific. doi:10.1142/9789811286018_0005. ISBN 978-981-12-8600-1.












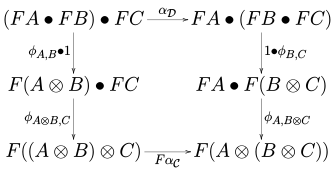





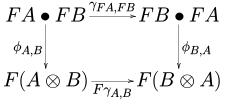














![{\displaystyle (Ch(R{\mathsf {-mod}}),\otimes ,R[0])\to (grR{\mathsf {-mod}},\otimes ,R[0])}](https://wikimedia.org/api/rest_v1/media/math/render/svg/5b5b3f3ab1c1e64cb4bc1848cedd0ae03b5e833f)
![{\displaystyle H_{\ast }(C_{1})\otimes H_{\ast }(C_{2})\to H_{\ast }(C_{1}\otimes C_{2}),[x_{1}]\otimes [x_{2}]\mapsto [x_{1}\otimes x_{2}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/88c1233008efff53b6dd10c40d0c790e60440b6c)











