Ramanujan–Soldner constant
This article relies largely or entirely on a single source. (April 2024) |
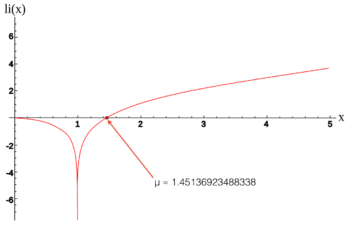
In mathematics, the Ramanujan–Soldner constant (also called the Soldner constant) is a mathematical constant defined as the unique positive zero of the logarithmic integral function. It is named after Srinivasa Ramanujan and Johann Georg von Soldner.
Its value is approximately μ ≈ 1.45136923488338105028396848589202744949303228… (sequence A070769 in the OEIS)
Since the logarithmic integral is defined by
then using we have
thus easing calculation for numbers greater than μ. Also, since the exponential integral function satisfies the equation
the only positive zero of the exponential integral occurs at the natural logarithm of the Ramanujan–Soldner constant, whose value is approximately ln(μ) ≈ 0.372507410781366634461991866… (sequence A091723 in the OEIS)
External links[edit]




