Architectonic and catoptric tessellation

In geometry, John Horton Conway defines architectonic and catoptric tessellations as the uniform tessellations (or honeycombs) of Euclidean 3-space with prime space groups and their duals, as three-dimensional analogue of the Platonic, Archimedean, and Catalan tiling of the plane. The singular vertex figure of an architectonic tessellation is the dual of the cell of the corresponding catoptric tessellation, and vice versa. The cubille is the only Platonic (regular) tessellation of 3-space, and is self-dual. There are other uniform honeycombs constructed as gyrations or prismatic stacks (and their duals) which are excluded from these categories.
Enumeration
[edit]The pairs of architectonic and catoptric tessellations are listed below with their symmetry group. These tessellations only represent four symmetry space groups, and also all within the cubic crystal system. Many of these tessellations can be defined in multiple symmetry groups, so in each case the highest symmetry is expressed.
| Ref.[1] indices |
Symmetry | Architectonic tessellation | Catoptric tessellation | ||||
|---|---|---|---|---|---|---|---|
| Name Coxeter diagram Image |
Vertex figure Image |
Cells | Name | Cell | Vertex figures | ||
| J11,15 A1 W1 G22 δ4 |
nc [4,3,4] |
Cubille (Cubic honeycomb) |
Octahedron, 
|
Cubille |
 Cube, |
||
| J12,32 A15 W14 G7 t1δ4 |
nc [4,3,4] |
Cuboctahedrille (Rectified cubic honeycomb) |
Cuboid, 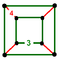
|
Oblate octahedrille |
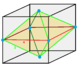 Isosceles square bipyramid |
||
| J13 A14 W15 G8 t0,1δ4 |
nc [4,3,4] |
Truncated cubille (Truncated cubic honeycomb) |
Isosceles square pyramid
|
Pyramidille |
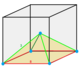 Isosceles square pyramid |
||
| J14 A17 W12 G9 t0,2δ4 |
nc [4,3,4] |
2-RCO-trille (Cantellated cubic honeycomb) |
Wedge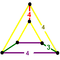
|
Quarter oblate octahedrille |
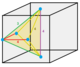 irr. Triangular bipyramid |
||
| J16 A3 W2 G28 t1,2δ4 |
bc [[4,3,4]] |
Truncated octahedrille (Bitruncated cubic honeycomb) |
Tetragonal disphenoid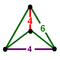
|
Oblate tetrahedrille |
 Tetragonal disphenoid |
||
| J17 A18 W13 G25 t0,1,2δ4 |
nc [4,3,4] |
n-tCO-trille (Cantitruncated cubic honeycomb) |
Mirrored sphenoid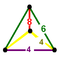
|
Triangular pyramidille |
 Mirrored sphenoid |
||
| J18 A19 W19 G20 t0,1,3δ4 |
nc [4,3,4] |
1-RCO-trille (Runcitruncated cubic honeycomb) |
Trapezoidal pyramid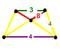
|
Square quarter pyramidille |
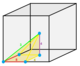 Irr. pyramid |
||
| J19 A22 W18 G27 t0,1,2,3δ4 |
bc [[4,3,4]] |
b-tCO-trille (Omnitruncated cubic honeycomb) |
Phyllic disphenoid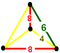
|
Eighth pyramidille |
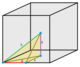 Phyllic disphenoid |
||
| J21,31,51 A2 W9 G1 hδ4 |
fc [4,31,1] |
Tetroctahedrille (Tetrahedral-octahedral honeycomb) |
Cuboctahedron, 
|
Dodecahedrille |
 Rhombic dodecahedron, |
||
| J22,34 A21 W17 G10 h2δ4 |
fc [4,31,1] |
truncated tetraoctahedrille (Truncated tetrahedral-octahedral honeycomb) |
Rectangular pyramid
|
Half oblate octahedrille |
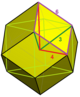 rhombic pyramid |
||
| J23 A16 W11 G5 h3δ4 |
fc [4,31,1] |
3-RCO-trille (Cantellated tetrahedral-octahedral honeycomb) |
Truncated triangular pyramid
|
Quarter cubille |
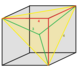 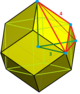 irr. triangular bipyramid |
||
| J24 A20 W16 G21 h2,3δ4 |
fc [4,31,1] |
f-tCO-trille (Cantitruncated tetrahedral-octahedral honeycomb) |
Mirrored sphenoid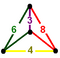
|
Half pyramidille |
 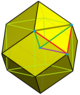 Mirrored sphenoid |
||
| J25,33 A13 W10 G6 qδ4 |
d [[3[4]]] |
Truncated tetrahedrille (Cyclotruncated tetrahedral-octahedral honeycomb) |
Isosceles triangular prism
|
Oblate cubille |
 Trigonal trapezohedron |
||
Vertex Figures
[edit]The vertex figures of all architectonic honeycombs, and the dual cells of all catoptric honeycombs are shown below, at the same scale and the same orientation:
Symmetry
[edit]
These four symmetry groups are labeled as:
| Label | Description | space group Intl symbol |
Geometric notation[2] |
Coxeter notation |
Fibrifold notation |
|---|---|---|---|---|---|
| bc | bicubic symmetry or extended cubic symmetry |
(221) Im3m | I43 | [[4,3,4]] |
8°:2 |
| nc | normal cubic symmetry | (229) Pm3m | P43 | [4,3,4] |
4−:2 |
| fc | half-cubic symmetry | (225) Fm3m | F43 | [4,31,1] = [4,3,4,1+] |
2−:2 |
| d | diamond symmetry or extended quarter-cubic symmetry |
(227) Fd3m | Fd4n3 | [[3[4]]] = [[1+,4,3,4,1+]] |
2+:2 |
References
[edit]- ^ For cross-referencing of Architectonic solids, they are given with list indices from Andreini (1-22), Williams(1-2,9-19), Johnson (11-19, 21-25, 31-34, 41-49, 51-52, 61-65), and Grünbaum(1-28). Coxeters names are based on δ4 as a cubic honeycomb, hδ4 as an alternated cubic honeycomb, and qδ4 as a quarter cubic honeycomb.
- ^ Hestenes, David; Holt, Jeremy (February 27, 2007). "Crystallographic space groups in geometric algebra" (PDF). Journal of Mathematical Physics. 48 (2). AIP Publishing LLC: 023514. doi:10.1063/1.2426416. ISSN 1089-7658. Archived from the original (PDF) on October 20, 2020. Retrieved April 9, 2013.
- Crystallography of Quasicrystals: Concepts, Methods and Structures by Walter Steurer, Sofia Deloudi (2009), p. 54-55. 12 packings of 2 or more uniform polyhedra with cubic symmetry
Further reading
[edit]- Conway, John H.; Burgiel, Heidi; Goodman-Strauss, Chaim (2008). "21. Naming Archimedean and Catalan Polyhedra and Tilings". The Symmetries of Things. A K Peters, Ltd. pp. 292–298. ISBN 978-1-56881-220-5.
- Inchbald, Guy (July 1997). "The Archimedean honeycomb duals". The Mathematical Gazette. 81 (491). Leicester: The Mathematical Association: 213–219. doi:10.2307/3619198. JSTOR 3619198. [1]
- Branko Grünbaum, (1994) Uniform tilings of 3-space. Geombinatorics 4, 49 - 56.
- Norman Johnson (1991) Uniform Polytopes, Manuscript
- A. Andreini, (1905) Sulle reti di poliedri regolari e semiregolari e sulle corrispondenti reti correlative (On the regular and semiregular nets of polyhedra and on the corresponding correlative nets), Mem. Società Italiana della Scienze, Ser.3, 14 75–129. PDF [2]
- George Olshevsky, (2006) Uniform Panoploid Tetracombs, Manuscript PDF [3]
- Pearce, Peter (1980). Structure in Nature is a Strategy for Design. The MIT Press. pp. 41–47. ISBN 9780262660457.
- Kaleidoscopes: Selected Writings of H. S. M. Coxeter, edited by F. Arthur Sherk, Peter McMullen, Anthony C. Thompson, Asia Ivic Weiss, Wiley-Interscience Publication, 1995, ISBN 978-0-471-01003-6 [4]
- (Paper 24) H.S.M. Coxeter, Regular and Semi-Regular Polytopes III, [Math. Zeit. 200 (1988) 3-45] See p318 [5]



