Резьбовое двоичное дерево

В вычислительной технике двоичное дерево с резьбой — это вариант двоичного дерева , который облегчает обход в определенном порядке.

Все двоичное дерево поиска можно легко обойти в порядке основного ключа, но, имея только указатель на узел , поиск следующего узла может быть медленным или невозможным. Например, листовые узлы по определению не имеют потомков, поэтому, имея только указатель на листовой узел, никакой другой узел не может быть достигнут. Дерево с резьбой добавляет дополнительную информацию в некоторые или все узлы, так что для любого отдельного узла можно быстро найти «следующий» узел, что позволяет обход дерева без рекурсии и дополнительное хранилище (пропорциональное глубине дерева), необходимое для рекурсии.

Резьба

«Двоичное дерево создается путем создания всех правых дочерних указателей, которые обычно имеют нулевое значение, указывающих на упорядоченного преемника узла ( если он существует), а все левые дочерние указатели, которые обычно имеют нулевое значение, указывают на упорядоченного предшественника. узла». ^[1]

Предполагается, что порядок обхода такой же, как и порядковый обход дерева. Однако указатели можно вместо (или в дополнение) добавлять к узлам дерева, а не заменять. Определенные таким образом связанные списки также обычно называются «потоками» и могут использоваться для обеспечения обхода в любом желаемом порядке. Например, дерево, узлы которого представляют информацию о людях, может быть отсортировано по имени, но иметь дополнительные потоки, позволяющие быстро перемещаться по дате рождения, весу или любой другой известной характеристике.

Мотивация

Деревья, включая (но не ограничиваясь) деревья двоичного поиска , могут использоваться для хранения элементов в определенном порядке, например, значения некоторого свойства, хранящегося в каждом узле, часто называемого ключом . Одной из полезных операций над таким деревом является обход : посещение всех элементов в порядке ключа.

Простой алгоритм рекурсивного обхода, который посещает каждый узел двоичного дерева поиска, заключается в следующем. Предположим, $t$ — указатель на узел или $nil$ . «Посещение» $t$ может означать выполнение любого действия над узлом $t$ или его содержимым.

Алгоритм обхода( $t$ ):

Входные данные: указатель $t$ на узел (или $nil$ ).
Если $t = nil$ , вернитесь.
Еще:
- траверс (левый ребенок ( $т$ ))
- Посетите $т$
- траверс (правый ребенок ( $т$ ))

Одна из проблем этого алгоритма заключается в том, что из-за его рекурсии он использует пространство стека, пропорциональное высоте дерева. Если дерево достаточно сбалансировано, это составляет $O (log n)$ пространства для дерева, содержащего $n$ элементов. В худшем случае, когда дерево принимает форму цепочки , высота дерева равна $n,$ поэтому алгоритм занимает $O (n)$ пространства. Вторая проблема заключается в том, что все обходы должны начинаться с корня, когда узлы имеют указатели только на своих дочерних элементов. Обычно имеется указатель на конкретный узел, но этого недостаточно для возврата к остальной части дерева, если не добавлена дополнительная информация, например указатели потоков.

При таком подходе может быть невозможно определить, действительно ли указатели слева и/или справа в данном узле указывают на дочерние элементы или являются следствием многопоточности. Если различие необходимо, для его записи достаточно добавить один бит к каждому узлу.

В учебнике 1968 года Дональд Кнут спросил, существует ли нерекурсивный алгоритм упорядоченного обхода, который не использует стек и оставляет дерево неизмененным. ^[2] Одним из решений этой проблемы является резьба деревьев, предложенная Джозефом М. Моррисом в 1979 году. ^[3]^[4]В последующем издании 1969 г. ^[5] Кнут приписал представление резьбового дерева Перлису и Торнтону (1960). ^[6]

Связь с родительскими указателями

Другой способ достижения аналогичных целей — включить в каждый узел указатель на родительский узел этого узла. Учитывая, что «следующий» узел всегда может быть достигнут, «правильные» указатели по-прежнему имеют значение null, когда нет правильных дочерних узлов. Чтобы найти «следующий» узел из узла, правый указатель которого равен нулю, пройдите вверх по «родительским» указателям, пока не достигнете узла, правый указатель которого не равен нулю и не является дочерним элементом, из которого вы только что вышли. Этот узел является «следующим» узлом, а за ним идут его потомки справа.

Также возможно обнаружить родителя узла из связанного двоичного дерева без явного использования родительских указателей или стека, хотя это медленнее. Чтобы убедиться в этом, рассмотрим узел k с правым дочерним элементом r . Тогда левый указатель r должен быть либо дочерним, либо обратным к k . В случае, когда r имеет левый дочерний элемент, этот левый дочерний элемент, в свою очередь, должен иметь либо собственный левый дочерний элемент, либо поток, возвращающийся к k , и так далее для всех последовательных левых дочерних элементов. Итак, следуя по цепочке левых указателей от r , мы в конечном итоге найдём поток, указывающий обратно на k . Ситуация симметрично аналогична, когда q является левым дочерним элементом p : мы можем проследить за правыми дочерними элементами q до потока, указывающего вперед на p .

В Питоне :

def parent(node):    if node is node.tree.root:        return None    x = node    y = node    while True:        if is_thread(y):            p = y.right            if p is None or p.left is not node:                p = x                while not is_thread(p.left):                    p = p.left                p = p.left            return p        elif is_thread(x):            p = x.left            if p is None or p.right is not node:                p = y                while not is_thread(p.right):                    p = p.right                p = p.right            return p        x = x.left        y = y.right

Типы

Однопоточный: каждый узел связан либо с преемником по порядку с предшествующим , либо (слева или справа).
Двойная резьба: каждый узел имеет резьбу как к предшественнику, так и к преемнику (слева и справа).

Массив упорядоченного обхода

Потоки относятся к предшественникам и преемникам узла в соответствии с упорядоченным обходом.

Порядковый обход резьбового дерева A,B,C,D,E,F,G,H,I, предшественник E является D, преемник E является F.

Пример

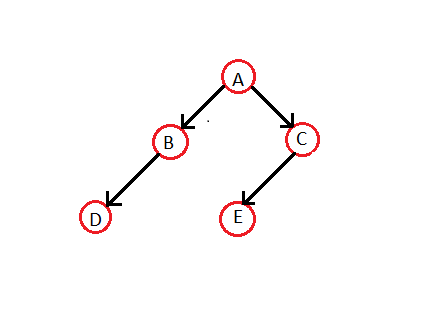
Давайте сделаем резьбовое двоичное дерево из обычного двоичного дерева:

Обход по порядку для вышеуказанного дерева — DBAE C. Таким образом, соответствующее двоичное дерево с резьбой будет —

Нулевые ссылки

В двоичном дереве с m -путями и n узлами имеется n × m − ( n −1) пустых связей.

Ссылки

^ Ван Вик, Кристофер Дж. Структуры данных и программы на C , Аддисон-Уэсли, 1988, стр. 175. ISBN 978-0-201-16116-8 .
^ Кнут, DE (1968). Фундаментальные алгоритмы . Искусство компьютерного программирования. Том. 1 (1-е изд.). Ридинг/Массачусетс: Эддисон Уэсли.
^ Моррис, Джозеф Х. (1979). «Обход бинарных деревьев просто и дешево». Письма об обработке информации . 9 (5). дои : 10.1016/0020-0190(79)90068-1 .
^ Матети, Прабхакер; Мангирмалани, Рави (1988). «Пересмотр алгоритма обхода дерева Морриса». Наука компьютерного программирования . 11 : 29–43. дои : 10.1016/0167-6423(88)90063-9 .
^ Кнут, DE (1969). Фундаментальные алгоритмы . Искусство компьютерного программирования. Том. 1 (2-е изд.). Эддисон Уэсли. Hre: Раздел 2.3.1 «Обход бинарных деревьев».
^ Перлис, Алан Джей; Торнтон, К. (апрель 1960 г.). «Манипулирование символами с помощью связанных списков» . Коммуникации АКМ . 3 (4): 195–204. дои : 10.1145/367177.367202 .

Внешние ссылки

GNU libavl 2.0.2, Раздел, посвященный многопоточным двоичным деревьям поиска

[1] Ван Вик, Кристофер Дж. Структуры данных и программы на C , Аддисон-Уэсли, 1988, стр. 175. ISBN 978-0-201-16116-8 .

[2] Кнут, DE (1968). Фундаментальные алгоритмы . Искусство компьютерного программирования. Том. 1 (1-е изд.). Ридинг/Массачусетс: Эддисон Уэсли.

[3] Моррис, Джозеф Х. (1979). «Обход бинарных деревьев просто и дешево». Письма об обработке информации . 9 (5). дои : 10.1016/0020-0190(79)90068-1 .

[4] Матети, Прабхакер; Мангирмалани, Рави (1988). «Пересмотр алгоритма обхода дерева Морриса». Наука компьютерного программирования . 11 : 29–43. дои : 10.1016/0167-6423(88)90063-9 .

[5] Кнут, DE (1969). Фундаментальные алгоритмы . Искусство компьютерного программирования. Том. 1 (2-е изд.). Эддисон Уэсли. Hre: Раздел 2.3.1 «Обход бинарных деревьев».

[6] Перлис, Алан Джей; Торнтон, К. (апрель 1960 г.). «Манипулирование символами с помощью связанных списков» . Коммуникации АКМ . 3 (4): 195–204. дои : 10.1145/367177.367202 .

[1]

[2]

[3]

[4]

[5]

[6]