Petrie dual
In topological graph theory, the Petrie dual of an embedded graph (on a 2-manifold with all faces disks) is another embedded graph that has the Petrie polygons of the first embedding as its faces.[1]
The Petrie dual is also called the Petrial, and the Petrie dual of an embedded graph may be denoted .[2] It can be obtained from a signed rotation system or ribbon graph representation of the embedding by twisting every edge of the embedding.
Properties
[edit]Like the usual dual graph, repeating the Petrie dual operation twice returns to the original surface embedding. Unlike the usual dual graph (which is an embedding of a generally different graph in the same surface) the Petrie dual is an embedding of the same graph in a generally different surface.[1]
Surface duality and Petrie duality are two of the six Wilson operations, and together generate the group of these operations.[3]
Regular polyhedra
[edit]Applying the Petrie dual to a regular polyhedron produces a regular map.[2] The number of skew h-gonal faces is g/2h, where g is the group order, and h is the coxeter number of the group.
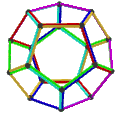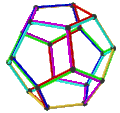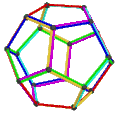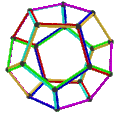
For example, the Petrie dual of a cube (a bipartite graph with eight vertices and twelve edges, embedded onto a sphere with six square faces) has four[4] hexagonal faces, the equators of the cube. Topologically, it forms an embedding of the same graph onto a torus.[1]
The regular maps obtained in this way are as follows.
- The petrial tetrahedron, {3,3}π, has 4 vertices, 6 edges, and 3 skew square faces. With an Euler characteristic, χ, of 1, it is topologically identical to the hemi-cube, {4,3}/2.
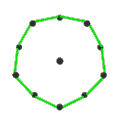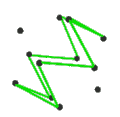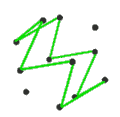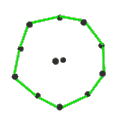
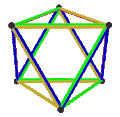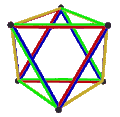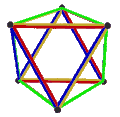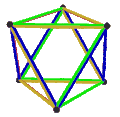
- The petrial cube, {4,3}π, has 8 vertices, 12 edges, and 4 skew hexagons, colored red, green, blue and orange here. With an Euler characteristic of 0, it can also be seen in the four hexagonal faces of the hexagonal tiling as type {6,3}(2,0).
- The petrial octahedron, {3,4}π, has 6 vertices, 12 edges, and 4 skew hexagon faces. It has an Euler characteristic of −2, and has a mapping to the hyperbolic order-4 hexagonal tiling, as type {6,4}3.
- The petrial dodecahedron, {5,3}π, has 20 vertices, 30 edges, and 6 skew decagonal faces, and Euler characteristic of −4, related to the hyperbolic tiling as type {10,3}5.
- The petrial icosahedron, {3,5}π, has 12 vertices, 30 edges, and 6 skew decagonal faces, and Euler characteristic of −12, related to the hyperbolic tiling as type {10,5}3.
| Name | Petrial tetrahedron |
Petrial cube |
Petrial octahedron |
Petrial dodecahedron |
Petrial icosahedron |
|---|---|---|---|---|---|
| Symbol | {3,3}π , {4,3}3 | {4,3}π , {6,3}4 | {3,4}π , {6,4}3 | {5,3}π , {10,3} | {3,5}π , {10,5} |
| (v,e,f), χ | (4,6,3), χ = 1 | (8,12,4), χ = 0 | (6,12,4), χ = −2 | (20,30,6), χ = −4 | (12,30,6), χ = −12 |
| Faces | 3 skew squares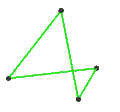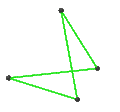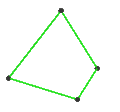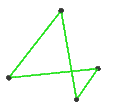
|
4 skew hexagons | 6 skew decagons | ||

|

|

|
| ||
| Image | 
|

|

|
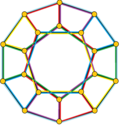
|

|
| Animation | 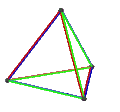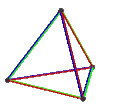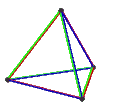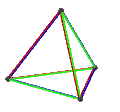
|

|
|
|
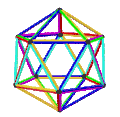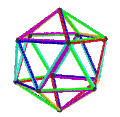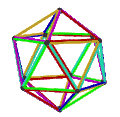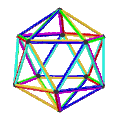
|
| Related figures |
 {4,3}3 = {4,3}/2 = {4,3}(2,0) |
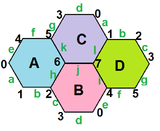 {6,3}3 = {6,3}(2,0) |
 {6,4}3 = {6,4}(4,0) |
{10,3}5 | {10,5}3 |
There are also 4 petrials of the Kepler–Poinsot polyhedra:
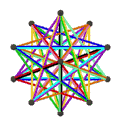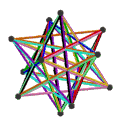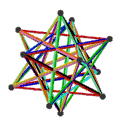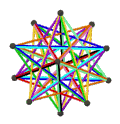
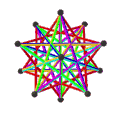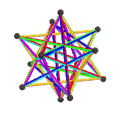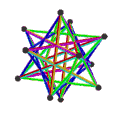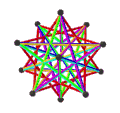
- The petrial great dodecahedron, {5,5/2}π, has 12 vertices, 30 edges, and 10 skew hexagon faces with an Euler characteristic, χ, of -8.
- The petrial small stellated dodecahedron, {5/2,5}π, has 12 vertices, 30 edges, and 10 skew hexagon faces with χ of -8.
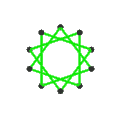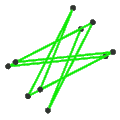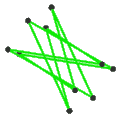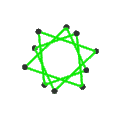
- The petrial great icosahedron, {3,5/2}π, has 12 vertices, 30 edges, and 6 skew decagram faces with χ of -12.
- The petrial great stellated dodecahedron, {5/2,3}π, has 20 vertices, 30 edges, and 6 skew decagram faces with χ of -4.
| Name | Petrial great dodecahedron |
Petrial small stellated dodecahedron |
Petrial great icosahedron |
Petrial great stellated dodecahedron |
|---|---|---|---|---|
| Symbol | {5,5/2}π , {6,5/2} | {5/2,5}π , {6,5} | {3,5/2}π , {10/3,5/2} | {5/2,3}π , {10/3,3} |
| (v,e,f), χ | (12,30,10), χ = -8 | (12,30,10), χ = -8 | (12,30,6), χ = -12 | (20,30,6), χ = -4 |
| Faces | 10 skew hexagons | 6 skew decagrams (one blue decagram outlined) | ||

|

|

|
| |
| Image | 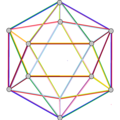
|

|

|

|
| Animation | 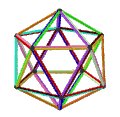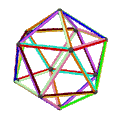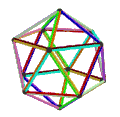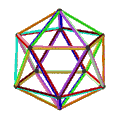
|
|
|

|
References
[edit]- ^ Jump up to: a b c Pisanski, Tomaž; Randić, Milan (2000), "Bridges between geometry and graph theory", in Gorini, Catherine A. (ed.), Geometry at work, MAA Notes, vol. 53, Washington, DC: Math. Assoc. America, pp. 174–194, MR 1782654. See in particular p. 181.
- ^ Jump up to: a b McMullen, Peter; Schulte, Egon (2002), Abstract Regular Polytopes, Encyclopedia of Mathematics and its Applications, vol. 92, Cambridge University Press, p. 192, ISBN 9780521814966
- ^ Jones, G. A.; Thornton, J. S. (1983), "Operations on maps, and outer automorphisms", Journal of Combinatorial Theory, Series B, 35 (2): 93–103, doi:10.1016/0095-8956(83)90065-5, MR 0733017
- ^ Octahedral symmetry is order 48, Coxeter number is 6, 48/(2×6)=4




