Inverse Gaussian distribution

For the distribution of 1/x when x is Gaussian, see Reciprocal normal distribution.

Inverse Gaussian

Probability density function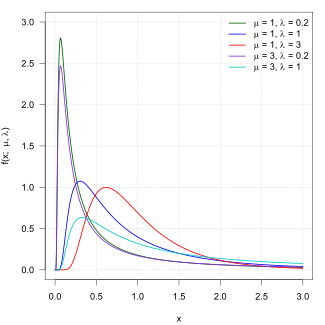
Cumulative distribution function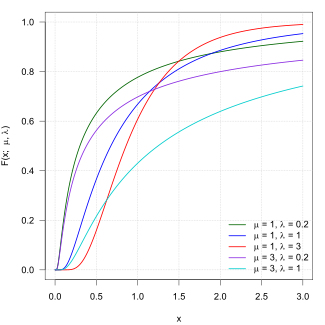
Notation	$\operatorname {IG} \left(\mu ,\lambda \right)$
Parameters	$\mu >0$ $\lambda >0$
Support	$x\in (0,\infty )$
PDF	${\sqrt {\frac {\lambda }{2\pi x^{3}}}}\exp \left[-{\frac {\lambda (x-\mu )^{2}}{2\mu ^{2}x}}\right]$
CDF	$\Phi \left({\sqrt {\frac {\lambda }{x}}}\left({\frac {x}{\mu }}-1\right)\right)$ ${}+\exp \left({\frac {2\lambda }{\mu }}\right)\Phi \left(-{\sqrt {\frac {\lambda }{x}}}\left({\frac {x}{\mu }}+1\right)\right)$ where $\Phi$ is the standard normal (standard Gaussian) distribution c.d.f.
Mean	$\operatorname {E} [X]=\mu$ $\operatorname {E} [{\frac {1}{X}}]={\frac {1}{\mu }}+{\frac {1}{\lambda }}$
Mode	$\mu \left[\left(1+{\frac {9\mu ^{2}}{4\lambda ^{2}}}\right)^{\frac {1}{2}}-{\frac {3\mu }{2\lambda }}\right]$
Variance	$\operatorname {Var} [X]={\frac {\mu ^{3}}{\lambda }}$ $\operatorname {Var} [{\frac {1}{X}}]={\frac {1}{\mu \lambda }}+{\frac {2}{\lambda ^{2}}}$
Skewness	$3\left({\frac {\mu }{\lambda }}\right)^{1/2}$
Excess kurtosis	${\frac {15\mu }{\lambda }}$
MGF	$\exp \left[{{\frac {\lambda }{\mu }}\left(1-{\sqrt {1-{\frac {2\mu ^{2}t}{\lambda }}}}\right)}\right]$
CF	$\exp \left[{{\frac {\lambda }{\mu }}\left(1-{\sqrt {1-{\frac {2\mu ^{2}\mathrm {i} t}{\lambda }}}}\right)}\right]$

In probability theory, the inverse Gaussian distribution (also known as the Wald distribution) is a two-parameter family of continuous probability distributions with support on (0,∞).

Its probability density function is given by

$f(x;\mu ,\lambda )={\sqrt {\frac {\lambda }{2\pi x^{3}}}}\exp {\biggl (}-{\frac {\lambda (x-\mu )^{2}}{2\mu ^{2}x}}{\biggr )}$

for x > 0, where $\mu >0$ is the mean and $\lambda >0$ is the shape parameter.

The inverse Gaussian distribution has several properties analogous to a Gaussian distribution. The name can be misleading: it is an "inverse" only in that, while the Gaussian describes a Brownian motion's level at a fixed time, the inverse Gaussian describes the distribution of the time a Brownian motion with positive drift takes to reach a fixed positive level.

Its cumulant generating function (logarithm of the characteristic function) is the inverse of the cumulant generating function of a Gaussian random variable.

To indicate that a random variable X is inverse Gaussian-distributed with mean μ and shape parameter λ we write $X\sim \operatorname {IG} (\mu ,\lambda )\,\!$.

Properties

Single parameter form

The probability density function (pdf) of the inverse Gaussian distribution has a single parameter form given by

$f(x;\mu ,\mu ^{2})={\frac {\mu }{\sqrt {2\pi x^{3}}}}\exp {\biggl (}-{\frac {(x-\mu )^{2}}{2x}}{\biggr )}.$

In this form, the mean and variance of the distribution are equal, $\mathbb {E} [X]={\text{Var}}(X).$

Also, the cumulative distribution function (cdf) of the single parameter inverse Gaussian distribution is related to the standard normal distribution by

${\begin{aligned}\Pr(X<x)&=\Phi (-z_{1})+e^{2\mu }\Phi (-z_{2}),\end{aligned}}$

where $z_{1}={\frac {\mu }{x^{1/2}}}-x^{1/2}$, $z_{2}={\frac {\mu }{x^{1/2}}}+x^{1/2},$ and the $\Phi$ is the cdf of standard normal distribution. The variables $z_{1}$ and $z_{2}$ are related to each other by the identity $z_{2}^{2}=z_{1}^{2}+4\mu .$

In the single parameter form, the MGF simplifies to

$M(t)=\exp[\mu (1-{\sqrt {1-2t}})].$

An inverse Gaussian distribution in double parameter form $f(x;\mu ,\lambda )$ can be transformed into a single parameter form $f(y;\mu _{0},\mu _{0}^{2})$ by appropriate scaling $y={\frac {\mu ^{2}x}{\lambda }},$ where $\mu _{0}=\mu ^{3}/\lambda .$

The standard form of inverse Gaussian distribution is

$f(x;1,1)={\frac {1}{\sqrt {2\pi x^{3}}}}\exp {\biggl (}-{\frac {(x-1)^{2}}{2x}}{\biggr )}.$

Summation

If X_i has an $\operatorname {IG} (\mu _{0}w_{i},\lambda _{0}w_{i}^{2})\,\!$ distribution for i = 1, 2, ..., n and all X_i are independent, then

$S=\sum _{i=1}^{n}X_{i}\sim \operatorname {IG} \left(\mu _{0}\sum w_{i},\lambda _{0}\left(\sum w_{i}\right)^{2}\right).$

Note that

${\frac {\operatorname {Var} (X_{i})}{\operatorname {E} (X_{i})}}={\frac {\mu _{0}^{2}w_{i}^{2}}{\lambda _{0}w_{i}^{2}}}={\frac {\mu _{0}^{2}}{\lambda _{0}}}$

is constant for all i. This is a necessary condition for the summation. Otherwise S would not be Inverse Gaussian distributed.

Scaling

For any t > 0 it holds that

$X\sim \operatorname {IG} (\mu ,\lambda )\,\,\,\,\,\,\Rightarrow \,\,\,\,\,\,tX\sim \operatorname {IG} (t\mu ,t\lambda ).$

Exponential family

The inverse Gaussian distribution is a two-parameter exponential family with natural parameters −λ/(2μ²) and −λ/2, and natural statistics X and 1/X.

For $\lambda >0$ fixed, it is also a single-parameter natural exponential family distribution where the base distribution has density

$h(x)={\sqrt {\frac {\lambda }{2\pi x^{3}}}}\exp \left(-{\frac {\lambda }{2x}}\right)\mathbb {1} _{[0,\infty )}(x)\,.$

Indeed, with $\theta \leq 0$,

$p(x;\theta )={\frac {\exp(\theta x)h(x)}{\int \exp(\theta y)h(y)dy}}$

is a density over the reals. Evaluating the integral, we get

$p(x;\theta )={\sqrt {\frac {\lambda }{2\pi x^{3}}}}\exp \left(-{\frac {\lambda }{2x}}+\theta x-{\sqrt {-2\lambda \theta }}\right)\mathbb {1} _{[0,\infty )}(x)\,.$

Substituting $\theta =-\lambda /(2\mu ^{2})$ makes the above expression equal to $f(x;\mu ,\lambda )$.

Relationship with Brownian motion

Example of stopped random walks with $\alpha =1,\nu =0.1,\sigma =0.2$. The upper figure shows the histogram of waiting times, along with the prediction according to inverse gaussian distribution. The lower figure shows the trajectories.

Let the stochastic process X_t be given by

$X_{0}=0\quad$

$X_{t}=\nu t+\sigma W_{t}\quad \quad \quad \quad$

where W_t is a standard Brownian motion. That is, X_t is a Brownian motion with drift $\nu >0$.

Then the first passage time for a fixed level $\alpha >0$ by X_t is distributed according to an inverse-Gaussian:

$T_{\alpha }=\inf\{t>0\mid X_{t}=\alpha \}\sim \operatorname {IG} \left({\frac {\alpha }{\nu }},\left({\frac {\alpha }{\sigma }}\right)^{2}\right)={\frac {\alpha }{\sigma {\sqrt {2\pi x^{3}}}}}\exp {\biggl (}-{\frac {(\alpha -\nu x)^{2}}{2\sigma ^{2}x}}{\biggr )}$

i.e

$P(T_{\alpha }\in (T,T+dT))={\frac {\alpha }{\sigma {\sqrt {2\pi T^{3}}}}}\exp {\biggl (}-{\frac {(\alpha -\nu T)^{2}}{2\sigma ^{2}T}}{\biggr )}dT$

(cf. Schrödinger equation 19, Smoluchowski, equation 8, and Folks, equation 1).

Derivation of the first passage time distribution

Suppose that we have a Brownian motion $X_{t}$ with drift $\nu$ defined by: $X_{t}=\nu t+\sigma W_{t},\quad X(0)=x_{0}$ And suppose that we wish to find the probability density function for the time when the process first hits some barrier $\alpha >x_{0}$ - known as the first passage time. The Fokker-Planck equation describing the evolution of the probability distribution $p(t,x)$ is: ${\partial p \over {\partial t}}+\nu {\partial p \over {\partial x}}={1 \over {2}}\sigma ^{2}{\partial ^{2}p \over {\partial x^{2}}},\quad {\begin{cases}p(0,x)&=\delta (x-x_{0})\\p(t,\alpha )&=0\end{cases}}$ where $\delta (\cdot )$ is the Dirac delta function. This is a boundary value problem (BVP) with a single absorbing boundary condition $p(t,\alpha )=0$, which may be solved using the method of images. Based on the initial condition, the fundamental solution to the Fokker-Planck equation, denoted by $\varphi (t,x)$, is: $\varphi (t,x)={1 \over {\sqrt {2\pi \sigma ^{2}t}}}\exp \left[-{(x-x_{0}-\nu t)^{2} \over {2\sigma ^{2}t}}\right]$ Define a point $m$, such that $m>\alpha$. This will allow the original and mirror solutions to cancel out exactly at the barrier at each instant in time. This implies that the initial condition should be augmented to become: $p(0,x)=\delta (x-x_{0})-A\delta (x-m)$ where $A$ is a constant. Due to the linearity of the BVP, the solution to the Fokker-Planck equation with this initial condition is: $p(t,x)={1 \over {\sqrt {2\pi \sigma ^{2}t}}}\left\{\exp \left[-{(x-x_{0}-\nu t)^{2} \over {2\sigma ^{2}t}}\right]-A\exp \left[-{(x-m-\nu t)^{2} \over {2\sigma ^{2}t}}\right]\right\}$ Now we must determine the value of $A$. The fully absorbing boundary condition implies that: $(\alpha -x_{0}-\nu t)^{2}=-2\sigma ^{2}t\log A+(\alpha -m-\nu t)^{2}$ At $p(0,\alpha )$, we have that $(\alpha -x_{0})^{2}=(\alpha -m)^{2}\implies m=2\alpha -x_{0}$. Substituting this back into the above equation, we find that: $A=e^{2\nu (\alpha -x_{0})/\sigma ^{2}}$ Therefore, the full solution to the BVP is: $p(t,x)={1 \over {\sqrt {2\pi \sigma ^{2}t}}}\left\{\exp \left[-{(x-x_{0}-\nu t)^{2} \over {2\sigma ^{2}t}}\right]-e^{2\nu (\alpha -x_{0})/\sigma ^{2}}\exp \left[-{(x+x_{0}-2\alpha -\nu t)^{2} \over {2\sigma ^{2}t}}\right]\right\}$ Now that we have the full probability density function, we are ready to find the first passage time distribution $f(t)$. The simplest route is to first compute the survival function $S(t)$, which is defined as: ${\begin{aligned}S(t)&=\int _{-\infty }^{\alpha }p(t,x)dx\\&=\Phi \left({\alpha -x_{0}-\nu t \over {\sigma {\sqrt {t}}}}\right)-e^{2\nu (\alpha -x_{0})/\sigma ^{2}}\Phi \left({-\alpha +x_{0}-\nu t \over {\sigma {\sqrt {t}}}}\right)\end{aligned}}$ where $\Phi (\cdot )$ is the cumulative distribution function of the standard normal distribution. The survival function gives us the probability that the Brownian motion process has not crossed the barrier $\alpha$ at some time $t$. Finally, the first passage time distribution $f(t)$ is obtained from the identity: ${\begin{aligned}f(t)&=-{dS \over {dt}}\\&={(\alpha -x_{0}) \over {\sqrt {2\pi \sigma ^{2}t^{3}}}}e^{-(\alpha -x_{0}-\nu t)^{2}/2\sigma ^{2}t}\end{aligned}}$ Assuming that $x_{0}=0$, the first passage time follows an inverse Gaussian distribution: $f(t)={\alpha \over {\sqrt {2\pi \sigma ^{2}t^{3}}}}e^{-(\alpha -\nu t)^{2}/2\sigma ^{2}t}\sim {\text{IG}}\left[{\alpha \over {\nu }},\left({\alpha \over {\sigma }}\right)^{2}\right]$

When drift is zero

A common special case of the above arises when the Brownian motion has no drift. In that case, parameter μ tends to infinity, and the first passage time for fixed level α has probability density function

$f\left(x;0,\left({\frac {\alpha }{\sigma }}\right)^{2}\right)={\frac {\alpha }{\sigma {\sqrt {2\pi x^{3}}}}}\exp \left(-{\frac {\alpha ^{2}}{2\sigma ^{2}x}}\right)$

(see also Bachelier). This is a Lévy distribution with parameters $c=\left({\frac {\alpha }{\sigma }}\right)^{2}$ and $\mu =0$.

Maximum likelihood

The model where

$X_{i}\sim \operatorname {IG} (\mu ,\lambda w_{i}),\,\,\,\,\,\,i=1,2,\ldots ,n$

with all w_i known, (μ, λ) unknown and all X_i independent has the following likelihood function

$L(\mu ,\lambda )=\left({\frac {\lambda }{2\pi }}\right)^{\frac {n}{2}}\left(\prod _{i=1}^{n}{\frac {w_{i}}{X_{i}^{3}}}\right)^{\frac {1}{2}}\exp \left({\frac {\lambda }{\mu }}\sum _{i=1}^{n}w_{i}-{\frac {\lambda }{2\mu ^{2}}}\sum _{i=1}^{n}w_{i}X_{i}-{\frac {\lambda }{2}}\sum _{i=1}^{n}w_{i}{\frac {1}{X_{i}}}\right).$

Solving the likelihood equation yields the following maximum likelihood estimates

${\widehat {\mu }}={\frac {\sum _{i=1}^{n}w_{i}X_{i}}{\sum _{i=1}^{n}w_{i}}},\,\,\,\,\,\,\,\,{\frac {1}{\widehat {\lambda }}}={\frac {1}{n}}\sum _{i=1}^{n}w_{i}\left({\frac {1}{X_{i}}}-{\frac {1}{\widehat {\mu }}}\right).$

${\widehat {\mu }}$ and ${\widehat {\lambda }}$ are independent and

${\widehat {\mu }}\sim \operatorname {IG} \left(\mu ,\lambda \sum _{i=1}^{n}w_{i}\right),\qquad {\frac {n}{\widehat {\lambda }}}\sim {\frac {1}{\lambda }}\chi _{n-1}^{2}.$

Sampling from an inverse-Gaussian distribution

The following algorithm may be used.

Generate a random variate from a normal distribution with mean 0 and standard deviation equal 1

$\displaystyle \nu \sim N(0,1).$

Square the value

$\displaystyle y=\nu ^{2}$

and use the relation

$x=\mu +{\frac {\mu ^{2}y}{2\lambda }}-{\frac {\mu }{2\lambda }}{\sqrt {4\mu \lambda y+\mu ^{2}y^{2}}}.$

Generate another random variate, this time sampled from a uniform distribution between 0 and 1

$\displaystyle z\sim U(0,1).$

If $z\leq {\frac {\mu }{\mu +x}}$ then return $\displaystyle x$ else return ${\frac {\mu ^{2}}{x}}.$

Sample code in Java:

public double inverseGaussian(double mu, double lambda) {
    Random rand = new Random();
    double v = rand.nextGaussian();  // Sample from a normal distribution with a mean of 0 and 1 standard deviation
    double y = v * v;
    double x = mu + (mu * mu * y) / (2 * lambda) - (mu / (2 * lambda)) * Math.sqrt(4 * mu * lambda * y + mu * mu * y * y);
    double test = rand.nextDouble();  // Sample from a uniform distribution between 0 and 1
    if (test <= (mu) / (mu + x))
        return x;
    else
        return (mu * mu) / x;
}

Wald distribution using Python with aid of matplotlib and NumPy

And to plot Wald distribution in Python using matplotlib and NumPy:

import matplotlib.pyplot as plt
import numpy as np

h = plt.hist(np.random.wald(3, 2, 100000), bins=200, density=True)

plt.show()

Related distributions

• If $X\sim \operatorname {IG} (\mu ,\lambda )$, then $kX\sim \operatorname {IG} (k\mu ,k\lambda )$ for any number $k>0.$
• If $X_{i}\sim \operatorname {IG} (\mu ,\lambda )\,$ then $\sum _{i=1}^{n}X_{i}\sim \operatorname {IG} (n\mu ,n^{2}\lambda )\,$
• If $X_{i}\sim \operatorname {IG} (\mu ,\lambda )\,$ for $i=1,\ldots ,n\,$ then ${\bar {X}}\sim \operatorname {IG} (\mu ,n\lambda )\,$
• If $X_{i}\sim \operatorname {IG} (\mu _{i},2\mu _{i}^{2})\,$ then $\sum _{i=1}^{n}X_{i}\sim \operatorname {IG} \left(\sum _{i=1}^{n}\mu _{i},2\left(\sum _{i=1}^{n}\mu _{i}\right)^{2}\right)\,$
• If $X\sim \operatorname {IG} (\mu ,\lambda )$, then $\lambda (X-\mu )^{2}/\mu ^{2}X\sim \chi ^{2}(1)$.

The convolution of an inverse Gaussian distribution (a Wald distribution) and an exponential (an ex-Wald distribution) is used as a model for response times in psychology, with visual search as one example.

History

This distribution appears to have been first derived in 1900 by Louis Bachelier as the time a stock reaches a certain price for the first time. In 1915 it was used independently by Erwin Schrödinger and Marian v. Smoluchowski as the time to first passage of a Brownian motion. In the field of reproduction modeling it is known as the Hadwiger function, after Hugo Hadwiger who described it in 1940. Abraham Wald re-derived this distribution in 1944 as the limiting form of a sample in a sequential probability ratio test. The name inverse Gaussian was proposed by Maurice Tweedie in 1945. Tweedie investigated this distribution in 1956 and 1957 and established some of its statistical properties. The distribution was extensively reviewed by Folks and Chhikara in 1978.

Numeric computation and software

Despite the simple formula for the probability density function, numerical probability calculations for the inverse Gaussian distribution nevertheless require special care to achieve full machine accuracy in floating point arithmetic for all parameter values. Functions for the inverse Gaussian distribution are provided for the R programming language by several packages including rmutil, SuppDists, STAR, invGauss, LaplacesDemon, and statmod.

See also

• Generalized inverse Gaussian distribution
• Tweedie distributions—The inverse Gaussian distribution is a member of the family of Tweedie exponential dispersion models
• Stopping time

Further reading

• Høyland, Arnljot; Rausand, Marvin (1994). System Reliability Theory. New York: Wiley. ISBN 978-0-471-59397-3.
• Seshadri, V. (1993). The Inverse Gaussian Distribution. Oxford University Press. ISBN 978-0-19-852243-0.

External links

• Inverse Gaussian Distribution in Wolfram website.