Доминатор (теория графов)

Не путать с доминирующим набором .

Пример графа потока управления с входным узлом 1

1	дом	1	2	3	4	5	6
2	дом		2	3	4	5	6
3	дом			3
4	дом				4
5	дом					5
6	дом						6
Соответствующее отношение доминирования: Серые узлы не доминируют строго Красные узлы сразу доминируют

Соответствующее дерево доминаторов графа потока управления

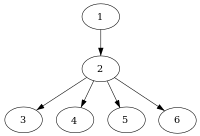
В информатике узел d должен доминирует графа потока управления над узлом n , если каждый путь от входного узла до n проходить через d . Условно это записывается как d dom n (или иногда d ≫ n ). По определению, каждый узел доминирует сам над собой.

Существует ряд связанных понятий:

• Узел d строго доминирует над узлом n, если d доминирует над n и d не равен n .
• или Непосредственный доминатор идом узла n — это уникальный узел, который строго доминирует над n, но не строго доминирует над каким-либо другим узлом, который строго доминирует над n . У каждого узла, кроме входного, есть непосредственный доминатор.
• Граница доминирования узла d — это набор всех узлов n _i таких, что d доминирует над непосредственным предшественником узла n _i , но d не доминирует строго над n _i . Это набор узлов, где . доминирование d прекращается
• Дерево -доминатор — это дерево , в котором дочерними узлами каждого узла являются те узлы, над которыми оно непосредственно доминирует. Начальный узел является корнем дерева.

История

Доминирование было впервые представлено Риз Т. Проссер в статье 1959 года об анализе блок-схем. Проссер не представил алгоритм вычисления доминирования, которого Эдварду С. Лоури и К. У. Медлоку пришлось ждать десять лет. Рон Сайтрон и др. возобновили интерес к доминированию в 1989 году, когда они применили его к проблеме эффективного вычисления размещения φ-функций, которые используются в статической форме с одним присваиванием .

Приложения

Доминаторы и, в частности, границы доминирования находят применение в компиляторах для вычисления статической формы одиночного присваивания . Ряд оптимизаций компилятора также могут выиграть от доминаторов. Граф потока в этом случае состоит из базовых блоков .

Доминаторы играют решающую роль в анализе потока управления, определяя поведение программы, соответствующее конкретному оператору или операции, что помогает оптимизировать и упростить поток управления программами для анализа.

Автоматическое распараллеливание выигрывает от границ постдоминирования. Это эффективный метод расчета зависимости управления, который имеет решающее значение для анализа.

Анализ использования памяти может помочь с использованием дерева доминаторов, позволяющего легко находить утечки и выявлять высокий уровень использования памяти.

В аппаратных системах доминаторы используются для вычисления вероятностей сигналов для генерации тестов, оценки активности переключения для анализа мощности и шума, а также выбора точек отсечения при проверке эквивалентности. В программных системах они используются для уменьшения размера набора тестов в методах структурного тестирования, таких как покрытие операторов и ветвей.

Алгоритмы

Позволять $n_{0}$ быть исходным узлом на графе потока управления . Доминаторы узла $n$ даются максимальным решением следующих уравнений потока данных:

$\operatorname {Dom} (n)={\begin{cases}\left\{n\right\}&{\mbox{ if }}n=n_{0}\\\left\{n\right\}\cup \left(\bigcap _{p\in {\text{preds}}(n)}^{}\operatorname {Dom} (p)\right)&{\mbox{ if }}n\neq n_{0}\end{cases}}$

Доминатором начального узла является сам начальный узел. Набор доминаторов для любого другого узла $n$ является пересечением множества доминаторов для всех предшественников $p$ из $n$. Узел $n$ также входит в набор доминаторов для $n$.

Алгоритм прямого решения:

 // dominator of the start node is the start itself Dom(n0) = {n0} // for all other nodes, set all nodes as the dominators for each n in N - {n0}     Dom(n) = N; // iteratively eliminate nodes that are not dominators while changes in any Dom(n)     for each n in N - {n0}:         Dom(n) = {n} union with intersection over Dom(p) for all p in pred(n)

Прямое решение квадратично по числу узлов, или O( n ² ). Ленгауэр и Тарьян разработали алгоритм, который является почти линейным. и на практике, за исключением нескольких искусственных графов, этот алгоритм и его упрощенная версия работают так же быстро или даже быстрее, чем любой другой известный алгоритм для графов всех размеров, и его преимущество увеличивается с размером графа.

Кит Д. Купер , Тимоти Дж. Харви и Кен Кеннеди из Университета Райса описывают алгоритм, который по существу решает приведенные выше уравнения потока данных, но использует хорошо спроектированные структуры данных для повышения производительности.

Постдоминирование

Аналогично определению доминирования, приведенному выше, узел z говорят, что пост-доминирует над узлом n, если все пути к выходному узлу графа, начинающиеся с n, должны проходить через z . Аналогично, непосредственный постдоминатор узла n — это постдоминатор узла n , который не строго постдоминирует над любыми другими строгими постдоминаторами узла n .

См. также

• Граф потока управления
• Интервал (теория графов)
• Статическая форма одиночного задания

Внешние ссылки

• Библиотека анализа потока управления Machine-SUIF