Стабилизированная обратная Q-фильтрация

Стабилизированная обратная Q-фильтрация — это технология обработки данных для повышения разрешения сейсмологических изображений отраженных волн, при которой учитывается стабильность используемого метода. Q — коэффициент неупругого затухания или сейсмическая добротность, мера потерь энергии при движении сейсмической волны. Чтобы получить решение, когда мы проводим расчеты с сейсмической моделью, нам всегда приходится учитывать проблему нестабильности и пытаться получить стабилизированное решение для сейсмической обратной Q-фильтрации .

Основы

Когда волна распространяется через подземные материалы, происходит как диссипация энергии, так и дисперсия скорости. Фильтрация обратной добротности — это метод восстановления потерь энергии из-за рассеяния энергии (амплитудная компенсация) и коррекции временного сдвига данных из-за дисперсии скорости.

Ван написал отличную книгу на тему обратной добротности-фильтрации « Сейсмическая обратная добротность-фильтрация» (2008) и обсудил тему стабилизации этого метода. Он пишет: «Упомянутый выше фазовый инверсный добротный фильтр безусловно стабилен. Однако, если включить в фильтр обратной добротности сопутствующую амплитудную компенсацию, стабильность станет серьезной проблемой при реализации».

Дом (1981) обнаружили, что фильтр обратной добротности сверхкомпенсировал амплитуды более поздних событий на сейсмической трассе. Следовательно, чтобы получить разумную амплитуду, амплитудный спектр вычисляемого фильтра должен быть ограничен при некотором максимальном усилении, чтобы предотвратить чрезмерную амплитуду в более поздние моменты времени. На основе этой концепции Ван предложил метод стабилизированной обратной добротности, позволяющий одновременно компенсировать как затухание, так и дисперсию». Необрезанная версия решения Ванга представлена ​​в статье в Википедии seismic inverse Q filtering . Решение основано на теории продолжения волнового поля вниз. В этом обзоре я буду вычислять урезанную версию, вводя фильтр нижних частот. И Хейл, и Ван представили фильтр нижних частот как метод стабилизации.

Расчеты

У нас есть уравнение для сейсмической обратной добротности фильтрации от Ванга:

$U(t+\bigtriangleup t,w)=U(t,w)\exp {\bigg (}|{\frac {w}{w_{r}}}|^{-\gamma }{\frac {|w|\bigtriangleup t}{2Q(w)}}{\bigg )}\exp {\bigg (}i|{\frac {w}{w_{r}}}|^{-\gamma }w\bigtriangleup t{\bigg )}\quad (1)$

$\gamma =(\pi Q_{r})^{-1}$

Время обозначается τ, частота — w, а i — мнимая единица. Q _r и w _r являются эталонными значениями, представляющими затухание и частоту для определенной частоты. Чтобы продемонстрировать стабильность, мы можем просто обойти использование опорной частоты и получить более простое уравнение:

$U(t+\bigtriangleup t,w)=U(t,w)\exp {\bigg (}{\frac {|w|\bigtriangleup t}{2Q(w)}}{\bigg )}\exp {\bigg (}iw\bigtriangleup t{\bigg )}\quad (2)$

Сумма этих плоских волн дает сейсмический сигнал во временной области:

$U(t+\bigtriangleup t)=\int _{0}^{\infty }U(t+\bigtriangleup t,w)dw.\quad (2.b)$

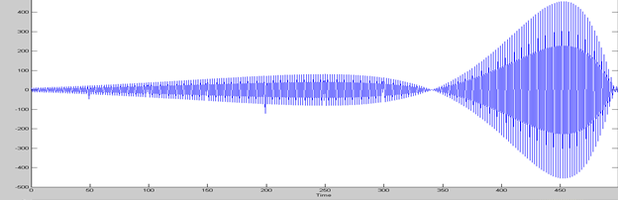
На рисунке 1 представлено решение (2/2.b) для сейсмической модели для различных значений Q, что ясно указывает на численную нестабильность. Число вверху рисунка 1 соответствует числу Q, 1=Q1, 2=Q2 и т. д. Результаты близки к результатам, представленным в книге Ванга (каждая трасса масштабируется индивидуально, поэтому артефакты на трассе 5 сильнее, чем на трассе 4). ). Однако Ван также рассматривал фазовую компенсацию. Расчеты здесь предназначены только для инверсии амплитуды, поскольку фазовая компенсация не требуется для демонстрации нестабильности, поскольку она всегда стабильна.

• 
  Рисунок 1. Кривые с обратной добротностью Q1=400,Q2=200,Q3=100,Q4=50,Q5=25

Фильтрация нижних частот и обратная добротность

На практике артефакты, вызванные числовой нестабильностью, можно подавить с помощью фильтра нижних частот. Хейл писал, что необрезанная IQF сейсмограммы увеличила частоту Найквиста в 7x10 раз. ⁶ когда мы имели соотношение t/Q=10 и пришли к выводу, что для типичных сейсмограмм с длиной более 1000 выборок и значением Q около 100 данные редко бывают достаточно чистыми, чтобы оправдать использование необрезанного IQF. Ван ввел частоту среза, чтобы установить критерий стабилизации с помощью математической формулы. Однако, учитывая статью Хейлза, может быть достаточно просто удалить частоту Найквиста. Это означает, что частота, близкая к частоте Найквиста, будет частотой среза. На рис.2 мы видим сейсмическую модель, предоставляющую нам контрольные данные для обратной Q-фильтрации (красный график). Мы увидим, что IQF этой модели усилит частоту Найквиста чуть менее чем в 5x10 раз. ⁶ .

• 
  Рисунок 2. Модель сейсмических эталонных данных. Зеленый график — незатухающий, красный — затухающий. Импульсная характеристика Q=50.

На рисунке 3 представлена ​​кривая с обратной добротностью, отфильтрованная только по амплитуде, показанная на рисунке 2 для Q = 50 (кривая 4). Результат ясно указывает на численную нестабильность. Артефакты видны по всей трассе.

• 
  Рис.3. Модель с рис.2. с применением инверсного Q-фильтра Q=50.

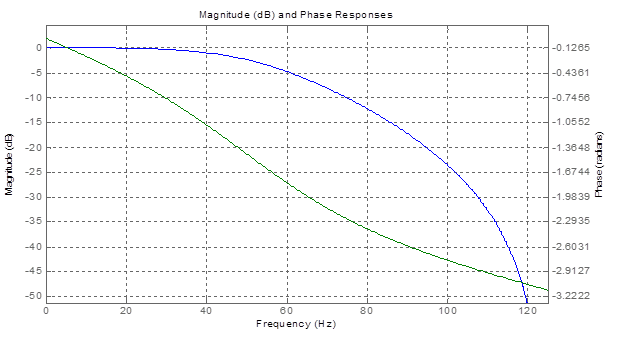
Мы попытаемся удалить артефакты, применив фильтр нижних частот к трассе, показанной на рисунке 3. Мы использовали инструмент обработки сигналов MATLABS и создали фильтр нижних частот (БИХ-фильтр с нулевой фазой) на рис. 4 с частотой среза 120. Гц. Амплитудная характеристика фильтра обозначена синим цветом, а фаза — зеленым.

• 
  Рис.4. Фильтр нижних частот

Результат фильтрации трассы на рис.3 с помощью фильтра нижних частот рис.4 показан на рис.5. Все артефакты удалены, и у нас остается импульсная характеристика, которую можно сравнить с исходной моделью на рис.2.

• 
  Рисунок 5. Отфильтрованные импульсные отклики, в которых удалена вся нестабильная энергия.

Частотная характеристика

Исследование частотной характеристики трассы рисунка 3 (необрезанного) и рисунка 5 (обрезанного) даст больше понимания процесса фильтрации. На рисунке 6 показана величина частотной характеристики как функция цифровой частоты до фильтрации. Это представление дает хорошее представление о том, что происходит вокруг частоты Найквиста, когда выполняется фильтрация с помощью фильтра нижних частот. Нестабильная энергия накапливается вблизи частоты Найквиста. После фильтрации нестабильная энергия вокруг частоты Найквиста полностью удаляется, и рис.7 дает частотную характеристику импульсной характеристики рис.5.

• 
  Рисунок 6. Частотная характеристика с цифровой частотой до фильтрации.

• 
  Рисунок 7. Частотная характеристика с цифровой частотой после фильтрации.

Ссылки

• Ван, Янхуа (2008). Сейсмическая обратная добротность-фильтрация . Паб Блэквелл. ISBN  978-1-4051-8540-0 .

Внешние ссылки

• Стабилизированная обратная добротность-фильтрация Кнута Сёрсдала