Кластеризация потоков данных

В информатике , кластеризация потоков данных определяется как кластеризация данных, которые поступают непрерывно, таких как телефонные записи, мультимедийные данные, финансовые транзакции и т. д. Кластеризация потоков данных обычно изучается как потоковый алгоритм и цель, учитывая последовательность точек, состоит в том, построить хорошую кластеризацию потока, используя небольшое количество памяти и времени.

История

Кластеризация потоков данных в последнее время привлекает внимание новых приложений, которые используют большие объемы потоковых данных. Для кластеризации широко используется эвристика k-means , но также были разработаны альтернативные алгоритмы, такие как k-medoids , CURE и популярный алгоритм. ^{[ нужна ссылка ]} БЕРЕЗА . Для потоков данных один из первых результатов появился в 1980 году. ^[1] но модель была формализована в 1998 году. ^[2]

Определение

Задача кластеризации потоков данных определяется как:

Входные данные: последовательность из n точек в метрическом пространстве и целое число k .
Выход: k центров в наборе из n точек, чтобы минимизировать сумму расстояний от точек данных до их ближайших центров кластеров.

Это потоковая версия проблемы k-медианы.

Алгоритмы

ТРАНСЛИРОВАТЬ

STREAM — это алгоритм кластеризации потоков данных, описанный Гухой, Мишрой, Мотвани и О'Каллаганом. ^[3] который обеспечивает аппроксимацию постоянного фактора для задачи k-медианы за один проход и с использованием небольшого пространства.

Теорема : STREAM может решить задачу k -медианы в потоке данных за один проход за время O ( n ^{1+ и}) и пространство θ ( n ^е) до коэффициента 2 ^{О(1/ е )}, где n количество точек и ⁠ $e<1/2$ ⁠ .

Чтобы понять STREAM, первым делом нужно показать, что кластеризация может осуществляться в небольшом пространстве (не заботясь о количестве проходов). Small-Space — это алгоритм «разделяй и властвуй» , который делит данные S на $\ell$ части, кластеризует каждую из них (используя k -средние), а затем кластеризует полученные центры.

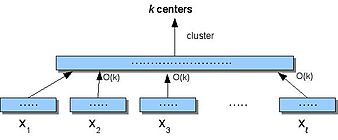
Представление алгоритма малого пространства

Алгоритм Small-Space(S)

Разделите S на $\ell$ непересекающиеся части $X_{1},\ldots ,X_{\ell }$ .
Для каждого i найдите ⁠ $O(k)$ ⁠ центры в X _i . Назначатькаждую точку Xi _{до ближайшего к ней} центра.
Пусть X' будет $O(\ell k)$ центры, полученные в (2),где каждый центр c имеет вес по числуприсвоенных ему баллов.
Кластер X', чтобы найти k центров.

Где, если на шаге 2 мы запускаем бикритерий ⁠ $(a,b)$ ⁠ - алгоритм аппроксимации , который выдает не более ak медиан со стоимостью, не более чем в b раз превышающей оптимальное решение k-медианы, и на шаге 4 мы запускаем алгоритм c -аппроксимации, тогда коэффициент аппроксимации алгоритма Small-Space() равен ⁠ $2c(1+2b)+2b$ ⁠ . Мы также можем обобщить Small-Space так, чтобы он рекурсивно вызывал себя i раз на последовательно меньшем наборе взвешенных центров и достигал аппроксимации с постоянным фактором для задачи k -медианы.

Проблема с Small-Space в том, что количество подмножеств $\ell$ то, на что мы разделяем S ограничено, поскольку оно должно хранить в памяти промежуточные медианы в X. , Итак, если M — размер памяти, нам нужно разделить S на $\ell$ подмножества так, что каждое подмножество умещается в памяти ( $n/\ell$ ) и так, чтобы взвешенный $\ell k$ центры также умещаются в памяти, $\ell k<M$ . Но такой $\ell$ может существовать не всегда.

Алгоритм STREAM решает проблему хранения промежуточных медиан и обеспечивает лучшие требования ко времени выполнения и пространству. Алгоритм работает следующим образом: ^[3]

Введите первые m точек; используя рандомизированный алгоритм, представленный в ^[3] сократите их до ⁠ $O(k)$ ⁠ (скажем, 2 тыс .) очков.
Повторяйте вышеописанное, пока мы не увидим м. ²/(2k ) исходных точек данных. Теперь у нас есть m промежуточных медиан.
Используя алгоритм локального поиска , сгруппируйте эти m медиан первого уровня в 2 тыс. медиан второго уровня и продолжайте.
В общем, поддерживайте не более m медиан уровня i и, увидев m , генерируйте 2 k медиан уровня i + 1 с весом новой медианы как суммой весов назначенных ей промежуточных медиан.
Когда мы увидели все исходные точки данных, мы группируем все промежуточные медианы в k окончательных медиан, используя основной двойной алгоритм. ^[4]

Другие алгоритмы

Другие известные алгоритмы, используемые для кластеризации потоков данных:

БЕРЕЗА : ^[5] строит иерархическую структуру данных для постепенной кластеризации входящих точек, используя доступную память и минимизируя требуемый объем ввода-вывода. Сложность алгоритма ⁠ $O(N)$ ⁠ поскольку для получения хорошей кластеризации достаточно одного прохода (хотя результаты можно улучшить, разрешив несколько проходов).
ПАУТИНКА : ^[6]^[7] — это метод инкрементной кластеризации, который сохраняет модель иерархической кластеризации в форме дерева классификации . Для каждой новой точки COBWEB спускается по дереву, по пути обновляет узлы и ищет лучший узел для размещения точки (используя служебную функцию категории ).
C2ICM : ^[8] строит плоскую структуру кластеризации с разделением, выбирая некоторые объекты в качестве начальных чисел/инициаторов кластера, а начальным числам назначается неначальное число, обеспечивающее максимальное покрытие. объекты и члены фальсифицированных кластеров присваиваются одному из существующих новых/старых начальных чисел.
КлуСтрим : ^[9] использует микрокластеры, которые являются временными расширениями BIRCH ^[5] вектор признаков кластера, чтобы он мог решить, может ли микрокластер быть вновь создан, объединен или забыт, на основе анализа квадрата и линейной суммы текущих точек данных и временных меток микрокластера, а затем в любой момент раз можно генерировать макрокластеры путем кластеризации этих микрокластеров с использованием алгоритма автономной кластеризации, такого как K-Means , что дает окончательный результат кластеризации.

Ссылки

^ Манро, Дж.; Патерсон, М. (1980). «Отбор и сортировка с ограниченным хранилищем» . Теоретическая информатика . 12 (3): 315–323. дои : 10.1016/0304-3975(80)90061-4 .
^ Хензингер, М.; Рагхаван, П.; Раджагопалан, С. (август 1998 г.). «Вычисления на потоках данных». Корпорация цифрового оборудования . ТР-1998-011. CiteSeerX 10.1.1.19.9554 .
^ Перейти обратно: ^а ^б ^с Гуха, С.; Мишра, Н.; Мотвани, Р.; О'Каллаган, Л. (2000). «Кластеризация потоков данных». Материалы 41-го ежегодного симпозиума по основам информатики . стр. 359–366. CiteSeerX 10.1.1.32.1927 . дои : 10.1109/SFCS.2000.892124 . ISBN 0-7695-0850-2 . S2CID 2767180 .
^ Джайн, К.; Вазирани, В. (1999). Алгоритмы первично-двойственной аппроксимации для решения задач размещения метрических объектов и задач k-медианы . Фокс '99. стр. 2–. ISBN 9780769504094 . {{cite book}}: |journal= игнорируется ( помогите )
^ Перейти обратно: ^а ^б Чжан, Т.; Рамакришнан, Р.; Линви, М. (1996). «BIRCH: эффективный метод кластеризации данных для очень больших баз данных» . Запись ACM SIGMOD . 25 (2): 103–114. дои : 10.1145/235968.233324 .
^ Фишер, Д.Х. (1987). «Получение знаний посредством поэтапной концептуальной кластеризации» . Машинное обучение . 2 (2): 139–172. дои : 10.1023/A:1022852608280 .
^ Фишер, Д.Х. (1996). «Итеративная оптимизация и упрощение иерархических кластеризаций». Журнал исследований искусственного интеллекта . 4 . arXiv : cs/9604103 . Бибкод : 1996cs........4103F . CiteSeerX 10.1.1.6.9914 .
^ Джан, Ф. (1993). «Инкрементальная кластеризация для динамической обработки информации» . Транзакции ACM в информационных системах . 11 (2): 143–164. дои : 10.1145/130226.134466 . S2CID 1691726 .
^ Аггарвал, Чару К.; Ю, Филип С.; Хан, Цзявэй; Ван, Цзянюн (2003). «Среда для кластеризации развивающихся потоков данных» (PDF) . Материалы конференции VLDB 2003 г .: 81–92. дои : 10.1016/B978-012722442-8/50016-1 . ISBN 9780127224428 . S2CID 2354576 .

[1] Манро, Дж.; Патерсон, М. (1980). «Отбор и сортировка с ограниченным хранилищем» . Теоретическая информатика . 12 (3): 315–323. дои : 10.1016/0304-3975(80)90061-4 .

[2] Хензингер, М.; Рагхаван, П.; Раджагопалан, С. (август 1998 г.). «Вычисления на потоках данных». Корпорация цифрового оборудования . ТР-1998-011. CiteSeerX 10.1.1.19.9554 .

[cds-3] Перейти обратно: ^а ^б ^с Гуха, С.; Мишра, Н.; Мотвани, Р.; О'Каллаган, Л. (2000). «Кластеризация потоков данных». Материалы 41-го ежегодного симпозиума по основам информатики . стр. 359–366. CiteSeerX 10.1.1.32.1927 . дои : 10.1109/SFCS.2000.892124 . ISBN 0-7695-0850-2 . S2CID 2767180 .

[4] Джайн, К.; Вазирани, В. (1999). Алгоритмы первично-двойственной аппроксимации для решения задач размещения метрических объектов и задач k-медианы . Фокс '99. стр. 2–. ISBN 9780769504094 . {{cite book}}: |journal= игнорируется ( помогите )

[birch-5] Перейти обратно: ^а ^б Чжан, Т.; Рамакришнан, Р.; Линви, М. (1996). «BIRCH: эффективный метод кластеризации данных для очень больших баз данных» . Запись ACM SIGMOD . 25 (2): 103–114. дои : 10.1145/235968.233324 .

[6] Фишер, Д.Х. (1987). «Получение знаний посредством поэтапной концептуальной кластеризации» . Машинное обучение . 2 (2): 139–172. дои : 10.1023/A:1022852608280 .

[7] Фишер, Д.Х. (1996). «Итеративная оптимизация и упрощение иерархических кластеризаций». Журнал исследований искусственного интеллекта . 4 . arXiv : cs/9604103 . Бибкод : 1996cs........4103F . CiteSeerX 10.1.1.6.9914 .

[8] Джан, Ф. (1993). «Инкрементальная кластеризация для динамической обработки информации» . Транзакции ACM в информационных системах . 11 (2): 143–164. дои : 10.1145/130226.134466 . S2CID 1691726 .

[9] Аггарвал, Чару К.; Ю, Филип С.; Хан, Цзявэй; Ван, Цзянюн (2003). «Среда для кластеризации развивающихся потоков данных» (PDF) . Материалы конференции VLDB 2003 г .: 81–92. дои : 10.1016/B978-012722442-8/50016-1 . ISBN 9780127224428 . S2CID 2354576 .

[1]

[2]

[3]

[4]

[5]

[6]

[7]

[8]

[9]