Маршрутизация противодавления

Термин «противодавление» при описании потока жидкости в трубопроводах и системах вентиляции воздуха см. в разделе « Противодавление » .

В теории массового обслуживания , дисциплине математической теории вероятностей , алгоритм маршрутизации противодавления — это метод направления трафика вокруг сети массового обслуживания, который обеспечивает максимальную пропускную способность сети. которое устанавливается с использованием представлений о дрейфе Ляпунова . Маршрутизация противодавления учитывает ситуацию, когда каждое задание может посещать несколько сервисных узлов в сети. Это расширение планирования максимального веса , при котором каждое задание посещает только один сервисный узел.

Введение

Маршрутизация с противодавлением — это алгоритм динамической маршрутизации трафика в сети с несколькими переходами с использованием градиентов перегрузки. Алгоритм может применяться к сетям беспроводной связи, включая сенсорные сети , мобильные одноранговые сети ( MANETS ), а также гетерогенные сети с беспроводными и проводными компонентами.

Принципы противодавления также можно применять и в других областях, например, в изучениисистемы сборки продукции и сети переработки. В этой статье основное внимание уделяется сетям связи,куда поступают пакеты из нескольких потоков данных идолжны быть доставлены в соответствующие пункты назначения. ПротиводавлениеАлгоритм работает в интервале времени. В каждом временном интервале он пытается направить данные в направлениях,максимизировать дифференциальное отставание между соседними узлами. Это похоже на то, как водатечет по сети труб через градиенты давления. Однако алгоритм противодавленияможет применяться к многопродуктовым сетям (где разные пакеты могут иметь разные пункты назначения),и к сетям, где можно выбирать скорость передачииз набора (возможно, изменяющихся во времени) опций. Привлекательные особенностиалгоритма противодавления: (i) он приводит к максимальной пропускной способности сети, (ii)он доказуемо устойчив к изменяющимся во времени условиям сети, (iii) онможет быть реализовано без знания скорости поступления трафика или состояния каналавероятности. Однако алгоритм может вносить большие задержки и можетбудет сложно реализовать именно в сетях с помехами. Модификациипротиводавление, которое уменьшает задержку и упрощает реализацию, описано нижепод Улучшение задержки и распределенного противодавления .

Маршрутизация противодавления в основном изучалась в теоретическом порядке.контекст. На практике одноранговые беспроводные сети обычно имеютреализованы альтернативные методы маршрутизации, основанные на кратчайшемвычисления пути или лавинная рассылка сети, например Специальная дистанционная векторная маршрутизация по требованию (AODV), географическая маршрутизация и чрезвычайно оппортунистическая маршрутизация (ExOR).Однако свойства математической оптимальности противодавлениямотивировали недавние экспериментальные демонстрации его использованияна испытательных стендах беспроводной связи в Университете Южной Калифорниии в Университете штата Северная Каролина.

Происхождение

Оригинальный алгоритм противодавления был разработан Тассиуласом и Эфремидом. Они рассмотрели многоскачковую пакетную радиосеть со случайным прибытием пакетов и фиксированным набором вариантов выбора канала. Их алгоритм состоял из этапа выбора канала с максимальным весом и этапа дифференциальной маршрутизации невыполненных задач .Алгоритм, связанный с противодавлением, предназначенный для расчета потоков многотоварной сети, был разработан в Авербухе и Лейтоне. Позднее Нили, Модиано и Рорс расширили алгоритм противодавления для планирования работы мобильных сетей. Противодавление математически анализируется с помощью теории дрейфа Ляпунова и может использоваться совместно с механизмами управления потоком для обеспечения максимизации полезности сети. (см. также «Обратное давление с оптимизацией утилит и минимизацией штрафов »).

Как это работает

Маршрутизация противодавления предназначена для принятия решений, которые (примерно) минимизируют сумму квадратов невыполненных очередей в сети от одного временного интервала к другому. Точное математическое развитие этого метода описано вболее поздние разделы. В этом разделе описывается общая модель сети и работа маршрутизации противодавления с учетомк этой модели.

Модель сети массового обслуживания с несколькими переходами

Рис. 1: 6-узловая многоскачковая сеть. Стрелки между узлами показывают текущих соседей.

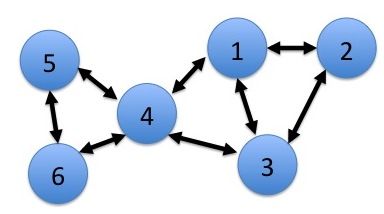
Рассмотрим многоскачковую сеть с N узлами (пример с N = 6 см. на рис. 1).Сеть работает вотведенное время $t\in \{0,1,2,\ldots \}$. В каждый слот могут поступать новые данныесети, а также принимаются решения о маршрутизации и планировании передачи.стремясь доставить все данные по назначению. Пусть данные, которым предназначенодля узла $c\in \{1,\dots ,N\}$ быть помечены как товар c данные . Данные в каждом узле хранятся в соответствии с его товаром. Для $n\in \{1,\ldots ,N\}$ и $c\in \{1,\ldots ,N\}$, позволять $Q_{n}^{(c)}(t)$ быть текущим объемом данных о товаре c в узле n , также называемом очередью . Крупный план невыполненных очередей внутри узла показан на рис. 2.Единицы $Q_{n}^{(c)}(t)$ зависят от контекста проблемы.Например, backlog может принимать целочисленные единицы пакетов , что полезно в случаях, когда данные сегментируются на пакеты фиксированной длины. Альтернативно, он может принимать действительные единицы битов . Предполагается, что $Q_{c}^{(c)}(t)=0$ для всех $c\in \{1,\ldots ,N\}$ и все временные интервалы t , поскольку ни один узел не хранит данные, предназначенные для него самого. В каждом временном интервале узлы могут передавать данные другим. Данные, которые передаются от одного узла к другому узлу, удаляются из очереди первого узла и добавляются в очередь второго. Данные, которые передаются по назначению, удаляются из сети. Данные также могут поступать в сеть экзогенно. $A_{n}^{(c)}(t)$ определяется как количество новых данных, поступающих в узел n в слоте t, которые в конечном итоге должныбыть доставлен в узел c .

Позволять $\mu _{ab}(t)$ быть скоростью передачи, используемой сетью по каналу ( a , b ) в слоте t , представляющей объем данных, которые она может передать от узла a к узлу b в текущем слоте. Позволять $(\mu _{ab}(t))$ быть матрицей скорости передачи. Эти скорости передачи должны выбираться из набора возможных вариантов, изменяющихся во времени. Конкретно,сеть может иметь изменяющиеся во времени каналы и узлымобильность, и это может повлиять на возможности передачи данных в каждом слоте.Чтобы смоделировать это, пусть S ( t ) представляет состояние топологии сети, которая фиксируетсвойства сети в слоте t , влияющие на передачу. Позволять $\Gamma _{S(t)}$ представлять наборвариантов матрицы скорости передачи, доступных в состоянии топологии S ( t ).В каждом слоте t сетевой контроллер наблюдает S ( t ) и выбирает передачуставки $(\mu _{ab}(t))$ в наборе $\Gamma _{S(t)}$.Выбор чего $(\mu _{ab}(t))$ матрицаВыбор в каждом слоте t описан в следующем подразделе.

Эта изменяющаяся во времени сетевая модель была впервые разработана для случая, когда скорость передачи в каждом слоте t определялась общими функциями матрицы состояния канала и матрицы распределения мощности. Модель также можно использовать, когда скорости определяются другими решениями управления, такими как распределение сервера, выбор поддиапазона, тип кодирования и т. д. Предполагается, что поддерживаемые скорости передачи известны и ошибок передачи нет. Расширенные формулировки маршрутизации с противодавлением могут использоваться для сетей с вероятностными ошибками канала, включая сети, которые используют преимущества беспроводного вещания за счет разнесения нескольких приемников .

Решения по управлению противодавлением

В каждом слоте t контроллер противодавления наблюдает за S ( t ) и выполняет следующие 3 шага:

• Сначала для каждого звена ( a , b ) он выбирает оптимальный товар. $c_{ab}^{opt}(t)$ использовать.
• Далее он определяет, что $(\mu _{ab}(t))$ матрица в $\Gamma _{S(t)}$ использовать.
• Наконец, он определяет количество товара $c_{ab}^{opt}(t)$ он будет передавать по ссылке ( a , b ) (не более $\mu _{ab}(t)$, но в некоторых случаях, возможно, меньше).

Выбор оптимального товара

Каждый узел a наблюдает за своими собственными невыполненными задачами в очереди и невыполненными задачами в своей текущейсоседи. Текущим соседом узла a является узел b такой, что можно выбратьненулевая скорость передачи $\mu _{ab}(t)$ в текущем слоте.Таким образом, соседи определяются множеством $\Gamma _{S(t)}$. В крайнем случае,узел может иметь в качестве соседей все N - 1 других узлов. Однако обычно используются наборы $\Gamma _{S(t)}$ которые исключают передачу между узлами, которые разделены более чем определенным географическим расстоянием,или уровень распространяемого сигнала будет ниже определенного порога.Таким образом, для числа соседей характернодолжно быть намного меньше, чем N - 1. Пример на рис. 1 иллюстрирует соседей по канальным соединениям, так что узел 5 имеет соседей 4 и 6. Пример предполагает симметричные отношения между соседями (так что, если 5 является соседом 4, тогда 4 является соседом 5), но в общем случае это не обязательно.

Набор соседей данного узла определяет набор исходящих каналов, которые он может использовать для передачи в текущем слоте. Для каждого исходящего звена ( a , b ) оптимальный товар $c_{ab}^{opt}(t)$ определяется как товар $c\in \{1,\ldots ,N\}$ что максимизирует следующий дифференциальный объем невыполненной работы:

$Q_{a}^{(c)}(t)-Q_{b}^{(c)}(t)$

Любые связи в выборе оптимального товара разрываются произвольно.

Рис. 2: Крупный план узлов 1 и 2. Оптимальный товар для отправки по ссылке (1,2) — зеленый товар. Оптимальный товар для отправки в обратном направлении (по ссылке (2,1)) — это синий товар.

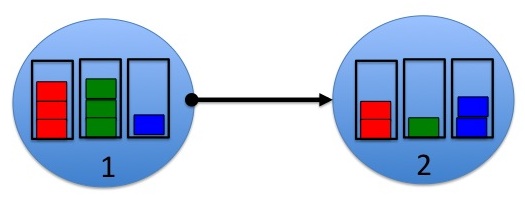
Пример показан на рис. 2. В примере предполагается, что каждая очередь в настоящее время содержит только 3 товара: красный , зеленый и blue , и они измеряются в целочисленных единицах пакетов. Ориентируясь на направленное звено (1,2), дифференциальные отставания составляют:

$Q_{1}^{({\text{red}})}(t)-Q_{2}^{({\text{red}})}(t)=1$

$Q_{1}^{({\text{green}})}(t)-Q_{2}^{({\text{green}})}(t)=2$

$Q_{1}^{({\text{blue}})}(t)-Q_{2}^{({\text{blue}})}(t)=-1$

Следовательно, оптимальным товаром для отправки по ссылке (1,2) в слоте t является зеленый товар. С другой стороны, оптимальным товаром для отправки по обратной ссылке (2,1) в слоте t является синий товар.

Выбор матрицы µ _ab ( t )

После того как оптимальные товары определены для каждого канала ( a , b ), сетевой контроллер вычисляет следующие веса: $W_{ab}(t)$:

$W_{ab}(t)=\max \left[Q_{a}^{(c_{ab}^{\mathrm {opt} }(t))}(t)-Q_{b}^{(c_{ab}^{opt}(t))}(t),0\right]$

Вес $W_{ab}(t)$ - это значение дифференциального отставания, связанного с оптимальным товаромдля канала ( a , b ), максимальное значение равно 0. Затем контроллер выбирает скорость передачи в качестве решенияследующая задача о максимальном весе (произвольно разрывая связи):

${\text{(Eq. 1)}}\qquad {\text{Maximize: }}\sum _{a=1}^{N}\sum _{b=1}^{N}\mu _{ab}(t)W_{ab}(t)$

${\text{(Eq. 2)}}\qquad {\text{Subject to: }}(\mu _{ab}(t))\in \Gamma _{S(t)}$

В качестве примера решения о максимальном весе предположим, что в текущем слоте t дифференциальные задержки на каждом канале сети из 6 узлов приводят к весам каналов. $W_{ab}(t)$ предоставлено:

$(W_{ab}(t))=\left[{\begin{array}{cccccc}0&2&1&1&6&0\\1&0&1&2&5&6\\0&7&0&0&0&0\\1&0&1&0&0&0\\1&0&7&5&0&0\\0&0&0&0&5&0\end{array}}\right]$

В то время как набор $\Gamma _{S(t)}$ может содержать несчетное бесконечное числовозможных матриц скорости передачи, для простоты предположим, что текущее состояние топологии допускает только 4 возможныхвыбор:

$\Gamma _{S(t)}=\{{\boldsymbol {\mu }}_{a},{\boldsymbol {\mu }}_{b},{\boldsymbol {\mu }}_{c},{\boldsymbol {\mu }}_{d}\}$

иллюстрация 4 возможных вариантов выбора скорости передачи в текущем состоянии топологии S ( t ). Опция (а) активируетсяодиночный канал (1,5) со скоростью передачи $\mu _{15}=2$. Все остальные варианты используют два канала со скоростью передачи 1 на каждом из активированных каналов.

Эти четыре возможности представлены в матричной форме следующим образом:

${\boldsymbol {\mu }}_{a}=\left[{\begin{array}{cccccc}0&0&0&0&2&0\\0&0&0&0&0&0\\0&0&0&0&0&0\\0&0&0&0&0&0\\0&0&0&0&0&0\\0&0&0&0&0&0\end{array}}\right],\quad {\boldsymbol {\mu }}_{b}=\left[{\begin{array}{cccccc}0&0&0&0&0&0\\0&0&1&0&0&0\\0&0&0&0&0&0\\0&0&0&0&1&0\\0&0&0&0&0&0\\0&0&0&0&0&0\end{array}}\right]$

${\boldsymbol {\mu }}_{c}=\left[{\begin{array}{cccccc}0&0&0&0&0&0\\1&0&0&0&0&0\\0&0&0&0&0&0\\0&0&0&0&1&0\\0&0&0&0&0&0\\0&0&0&0&0&0\end{array}}\right],\quad {\boldsymbol {\mu }}_{d}=\left[{\begin{array}{cccccc}0&0&0&0&0&0\\0&0&0&0&0&0\\0&1&0&0&0&0\\0&0&0&0&0&0\\0&0&0&1&0&0\\0&0&0&0&0&0\end{array}}\right]$

Обратите внимание, что узел 6 не может ни отправлять, ни получать ни при одной из этих возможностей.Это может произойти из-за того, что узел 6 в настоящее время находится вне зоны действия связи.Взвешенная сумма ставок для каждой из 4 возможностей составляет:

• Вариант (а): $\sum _{ab}W_{ab}(t)\mu _{ab}(t)=12$.
• Вариант (б): $\sum _{ab}W_{ab}(t)\mu _{ab}(t)=1$.
• Выбор (с): $\sum _{ab}W_{ab}(t)\mu _{ab}(t)=1$.
• Выбор (г): $\sum _{ab}W_{ab}(t)\mu _{ab}(t)=12$.

Поскольку существует ничья для максимального веса 12, сетевой контроллер может произвольно разорвать эту связь,выбирая любой вариант ${\boldsymbol {\mu }}_{a}$ или вариант ${\boldsymbol {\mu }}_{d}$.

Завершение переменных маршрутизации

Предположим теперь, что оптимальные товары $c_{ab}^{opt}(t)$были определены для каждого звена, а передачаставки $(\mu _{ab}(t))$ также были определены.Если дифференциальное отставание для оптимального товара по данному звену ( a , b ) отрицательное, то данные не передаются.по этой ссылке в текущем слоте. В противном случае сеть предлагает отправить $\mu _{ab}(t)$ единицы товара $c_{ab}^{\mathrm {opt} }(t)$данные по этой ссылке. Это делается путем определения переменных маршрутизации $\mu _{ab}^{(c)}(t)$ для каждой ссылки ( a , b ) икаждый товар c , где:

$\mu _{ab}^{(c)}(t)={\begin{cases}\mu _{ab}(t)&{\text{ if }}c=c_{ab}^{opt}(t){\text{ and }}Q_{a}^{(c_{ab}^{opt}(t))}(t)-Q_{b}^{(c_{ab}^{opt}(t))}(t)\geq 0\\0&{\text{ otherwise}}\end{cases}}$

Стоимость $\mu _{ab}^{(c)}(t)$ представляет скорость передачи данных товара c по каналу связи( a , b ) в слоте t .Однако узлам может не хватать определенного товара для поддержки передачи.по предлагаемым тарифам на все исходящие ссылки. Это возникает в слоте t для узла n и товара c, если:

$Q_{n}^{(c)}(t)<\sum _{b=1}^{N}\mu _{nb}^{(c)}(t)$

В этом случае все $Q_{n}^{(c)}(t)$ данные отправляются, а нулевые данные используются для заполнения неиспользованных частей предлагаемых тарифов,произвольное распределение фактических данных и нулевых данных по соответствующим исходящим каналам (согласно предлагаемым тарифам).Это называется ситуацией переполнения очереди . Такие потери не влияют на пропускную способность.или свойства стабильности сети. Интуитивно это происходит потому, чтовозникают только тогда, когда передающий узел имеет небольшое количество отставания, что означает, чтоузлу не грозит нестабильность.

Улучшение задержки

Алгоритм противодавления не использует заранее заданные пути. Пути изученыдинамически и может быть разным для разных пакетов. Задержка может быть очень большой, особенно когда система слегказагружен так, что не хватает давления для передачи данных к месту назначения. В качестве примера предположим, что один пакетвходит в сеть, и больше ничего не входит. Этот пакет может совершить закольцованное путешествие по сети и так и не прийти.в пункте назначения, поскольку не возникает градиентов давления. Это не противоречит оптимальности и стабильности пропускной способности.свойства противодавления, поскольку сеть имеет не более одного пакета в любой момент времени и, следовательно, является тривиально стабильной (достижение скорости доставки 0, равной скорости поступления).

Также возможно реализовать противодавление по набору заранее заданных путей. Это может ограничить область емкости, но может улучшитьдоставка и задержка. Другой способ улучшить задержку, не затрагивая область пропускной способности, — использовать расширенный версия, которая смещает вес ссылок в желательном направлении. Моделирование такого смещения показало значительные улучшения задержки. Обратите внимание, что противодавление не требует обслуживания в порядке ( FIFO очереди ). Было замеченочто служба Last-in-First-Out ( LIFO ) может значительно улучшить задержку для подавляющего большинства пакетов,без влияния на пропускную способность.

Распределенное противодавление

Обратите внимание, что как только скорость передачи $(\mu _{ab}(t))$ были выбраны, переменные решения маршрутизации $\mu _{ab}^{(c)}(t)$могут быть вычислены простым распределенным способом, где каждый узел требует только знанияразница в очереди в очереди между собой и своими соседями. Однако выбор скоростей передачи требует решенияпроблема максимального веса в уравнениях. (1)-(2). В частном случае, когда каналы ортогональны, алгоритм имеет естественную распределенную реализацию и сводится к раздельным решениям в каждом узле. Однако проблема максимального веса является проблемой централизованного управления для сетей с межканальными помехами. Это также может быть очень сложно решить даже централизованно.

Распределенный подход для сетей с помехами, скорость соединения которых определяется отношением сигнал/шум плюс помехи (SINR), может быть реализована с использованием рандомизации. Каждый узел случайным образом решает передать каждый слот t (передавая «нулевой» пакет, если в данный момент он этого не делает).есть пакет для отправки). Фактическая скорость передачи и соответствующие фактические пакеты для отправки.определяются двухэтапным рукопожатием:На первом этапе случайно выбранные узлы передатчика отправляют пилот-сигнал с уровнем сигнала, пропорциональнымк фактической передаче. На втором шаге,все потенциальные узлы-приемники измеряют возникающие помехи и отправляют эту информацию обратно впередатчики. Уровни SINR для всех исходящих каналов ( n , b ) затем известны всем узлам n ,и каждый узел n может решитьего $\mu _{nb}(t)$ и $(\mu _{nb}^{(c)}(t))$ переменные на основе этой информации.Полученная пропускная способность не обязательно является оптимальной. Однако процесс случайной передачи можно рассматривать как часть процесса состояния канала (при условии, что нулевые пакеты отправляются в случаях недостаточного заполнения, так что процесс состояния канала не зависит от прошлых решений). Следовательно, результирующая пропускная способность этой распределенной реализации оптимальна для класса всех алгоритмов маршрутизации и планирования, которые используют такие рандомизированные передачи.

Альтернативные распределенные реализации можно грубо сгруппировать в два класса:Первый класс алгоритмов рассматривает приближения постоянного мультипликативного фактора к проблеме максимального веса:и дают результаты производительности с постоянным коэффициентом. Второй класс алгоритмов рассматривает аддитивные аппроксимации максимального весапроблема, основанная на обновлении решений проблемы максимального веса с течением времени. Алгоритмы этого второго класса, похоже, требуют статического канала.условия и более длительное (часто неполиномиальное) время сходимости, хотя они доказуемо могут обеспечить максимальную пропускную способность.при соответствующих предположениях. Аддитивные приближения часто бывают полезны.для доказательства оптимальности противодавления при реализации с устаревшей информацией об очереди (см. упражнение 4.10 из текста Нили).

Математическое построение с помощью дрейфа Ляпунова

В этом разделе показано, как алгоритм противодавления возникает как естественное следствиежадно минимизируя границу изменения суммы квадратов невыполненных очередей от одного слота к другому.

Ограничения на решение по управлению и уравнение обновления очереди

Рассмотрим сеть с несколькими переходами и N узлами, как описано в разделе выше.В каждом слоте t сетевой контроллер наблюдает за состоянием топологии S ( t ) и выбираетскорость передачи $(\mu _{ab}(t))$ и переменные маршрутизации $(\mu _{ab}^{(c)}(t))$ предметк следующим ограничениям:

${\text{(Eq. 3)}}\qquad (\mu _{ab}(t))\in \Gamma _{S(t)}$

${\text{(Eq. 4)}}\qquad 0\leq \mu _{ab}^{(c)}(t)\qquad \forall a,b,c,\forall t$

${\text{(Eq. 5)}}\qquad \sum _{c=1}^{N}\mu _{ab}^{(c)}(t)\leq \mu _{ab}(t)\qquad \forall (a,b),\forall t$

Как только эти переменные маршрутизации определены, выполняются передачи (при необходимости с использованием простоя заполнения), и результирующая очередьневыполненные работы удовлетворяют следующему:

${\text{(Eq. 6)}}\qquad Q_{n}^{(c)}(t+1)\leq \max \left[Q_{n}^{(c)}(t)-\sum _{b=1}^{N}\mu _{nb}^{(c)}(t),0\right]+\sum _{a=1}^{N}\mu _{an}^{(c)}(t)+A_{n}^{(c)}(t)$

где $A_{n}^{(c)}(t)$ случайное количество нового товара c данные, которые экзогенно поступают в узел n в слоте t , и $\mu _{nb}^{(c)}(t)$ выделенная скорость передачик трафику товара c по ссылке ( n , b ) в слоте t . Обратите внимание, что $\mu _{nb}^{(c)}(t)$ может быть больше суммы данные товара c, которые фактически передаются по ссылке ( a , b ) в слоте t . Это потому, что может не хватить отставанияв узле n . По этой же причине уравнение. (6) является неравенством, а не равенством, поскольку $\sum _{a=1}^{N}\mu _{an}^{(c)}(t)$ может быть больше, чем фактическое эндогенное поступление товара c в узел n в слоте t .Важная особенность уравнения. (6) заключается в том, что оно справедливо, даже если $\mu _{ab}^{(c)}(t)$ переменные решения выбираются независимо от невыполненной очереди.

Предполагается, что $Q_{c}^{(c)}(t)=0$ для всех слотов т и все $c\in \{1,\ldots ,N\}$, поскольку ни одна очередь не хранит данные, предназначенные для самой себя.

Ляпуновский занос

Определять ${\boldsymbol {Q}}(t)=(Q_{n}^{(c)}(t))$ как матрица текущих невыполненных очередей.Определим следующую неотрицательную функцию, называемую функцией Ляпунова :

$L(t)={\frac {1}{2}}\sum _{n=1}^{N}\sum _{c=1}^{N}Q_{n}^{(c)}(t)^{2}$

Это сумма квадратов невыполненных очередей (умноженная на 1/2 только для удобства при дальнейшем анализе). Приведенная выше сумма аналогична суммированию по всем n , c таким, что $n\neq c$ потому что $Q_{c}^{(c)}(t)=0$ для всех $c\in \{1,\ldots ,N\}$ и все слоты т .

Условный дрейф Ляпунова $\Delta (t)$ определяется:

$\Delta (t)=E\left[L(t+1)-L(t)\mid {\boldsymbol {Q}}(t)\right]$

Заметим, что следующее неравенство справедливо для всех $q\geq 0$, $a\geq 0$, $b\geq 0$:

$(\max[q-b,0]+a)^{2}\leq q^{2}+b^{2}+a^{2}+2q(a-b)$

Возведя в квадрат уравнение обновления очереди (уравнение (6)) и используя приведенное выше неравенство, нетруднопоказать, что для всех слотов t и при любом алгоритме выбора переменных передачи и маршрутизации $(\mu _{ab}(t))$и $(\mu _{ab}^{(c)}(t))$:

${\text{(Eq. 7)}}\qquad \Delta (t)\leq B+\sum _{n=1}^{N}\sum _{c=1}^{N}Q_{n}^{(c)}(t)E\left[\lambda _{n}^{(c)}(t)+\sum _{a=1}^{N}\mu _{an}^{(c)}(t)-\sum _{b=1}^{N}\mu _{nb}^{(c)}(t)|{\boldsymbol {Q}}(t)\right]$

где B — конечная константа, зависящая от вторых моментов поступления и максимально возможных вторых моментов скорости передачи.

Минимизация дрейфа путем переключения сумм

Алгоритм противодавления предназначен для наблюдения ${\boldsymbol {Q}}(t)$ и S ( t ) в каждом слоте t и выберите $(\mu _{ab}(t))$ и $(\mu _{ab}^{(c)}(t))$ чтобы минимизировать правую часть границы дрейфа (уравнение). (7). Поскольку B является константой и $\lambda _{n}^{(c)}$ являются константами, это означает максимизацию:

$E\left[\sum _{n=1}^{N}\sum _{c=1}^{N}Q_{n}^{(c)}(t)\left[\sum _{b=1}^{N}\mu _{nb}^{(c)}(t)-\sum _{a=1}^{N}\mu _{an}^{(c)}(t)\right]|{\boldsymbol {Q}}(t)\right]$

где конечные суммы были пропущены через ожидания, чтобы пролить свет на максимизирующее решение.Согласно принципу оппортунистической максимизации ожидания , вышеуказанное ожидание максимизируется путеммаксимизируя функцию внутри него (с учетом наблюдаемого ${\boldsymbol {Q}}(t)$, $S(t)$).Таким образом, человек выбирает $(\mu _{ab}(t))$ и $(\mu _{ab}^{(c)}(t))$с учетом ограничений (уравнений). (3)-(5) для максимизации:

$\sum _{n=1}^{N}\sum _{c=1}^{N}Q_{n}^{(c)}(t)\left[\sum _{b=1}^{N}\mu _{nb}^{(c)}(t)-\sum _{a=1}^{N}\mu _{an}^{(c)}(t)\right]$

Не сразу очевидно, какие решения максимизируют вышеизложенное. Это можно прояснить, переключая суммы.Действительно, приведенное выше выражение такое же, как и ниже:

$\sum _{a=1}^{N}\sum _{b=1}^{N}\sum _{c=1}^{N}\mu _{ab}^{(c)}(t)[Q_{a}^{(c)}(t)-Q_{b}^{(c)}(t)]$

Вес $Q_{a}^{(c)}(t)-Q_{b}^{(c)}(t)$ называется текущим дифференциальным отставанием товара c междуузлы а и б . Идея состоит в том, чтобы выбрать переменные решения $(\mu _{ab}^{(c)}(t))$ чтобы максимизировать вышеизложенноевзвешенная сумма, где веса представляют собой дифференциальные резервы. Интуитивно это означает выделение более высоких ставок по направлениямбольшего дифференциального отставания.

Очевидно, что следует выбрать $\mu _{ab}^{(c)}(t)=0$в любое время $Q_{a}^{(c)}(t)-Q_{b}^{(c)}(t)<0$. Далее, учитывая $\mu _{ab}(t)$ по конкретной ссылке $(a,b)$,нетрудно показать, что оптимальное $\mu _{ab}^{(c)}(t)$ выборы,с учетом уравнений (3)-(5),определяются следующим образом: сначала находят товар $c_{ab}^{opt}(t)\in \{1,\ldots ,N\}$это максимизирует дифференциальное отставание для ссылки ( a , b ).Если максимизирующее дифференциальное отставание отрицательно для ссылки ( a , b ),назначать $\mu _{ab}^{(c)}(t)=0$ для всех товаров $c\in \{1,\ldots ,N\}$по ссылке ( а , б ). В противном случае выделите полную скорость ссылки. $\mu _{ab}(t)$ к товару $c_{ab}^{opt}(t)$и нулевую ставку для всех остальных товаров по этой ссылке. Из этого выбора следует, что:

$\sum _{c=1}^{N}\mu _{ab}^{(c)}(t)[Q_{a}^{(c)}(t)-Q_{b}^{(c)}(t)]=\mu _{ab}(t)W_{ab}(t)$

где $W_{ab}(t)$ — дифференциальное отставание оптимального товара для ссылки ( a , b ) в слоте t (максимум 0):

$W_{ab}(t)=\max[Q_{a}^{(c_{ab}^{opt}(t))}(t)-Q_{b}^{(c_{ab}^{opt}(t))}(t),0]$

Осталось только выбрать $(\mu _{ab}(t))\in \Gamma _{S(t)}$. Это достигается путем решения следующих задач:

$\mathrm {Maximize:} \sum _{a=1}^{N}\sum _{b=1}^{N}\mu _{ab}(t)W_{ab}(t)$

$\mathrm {Subjectto:} (\mu _{ab}(t))\in \Gamma _{S(t)}$

Вышеупомянутая проблема идентична проблеме максимального веса в уравнениях. (1)-(2).Алгоритм противодавления использует решения о максимальном весе для $(\mu _{ab}(t))$, а затем выбирает переменные маршрутизации $(\mu _{ab}^{(c)}(t))$ через максимальное дифференциальное отставание, как описано выше.

Замечательным свойством алгоритма противодавления является то, что он действует жадно в каждом слоте t, основываясь только на наблюдаемом состоянии топологии S ( t ) и невыполненных очередях. ${\boldsymbol {Q}}(t)$ для этого слота. Таким образом, не требуется знание скоростей поступления $(\lambda _{n}^{(c)})$ или вероятности состояния топологии $\pi _{S}=Pr[S(t)=S]$.

Анализ производительности

В этом разделе доказывается оптимальность пропускной способности алгоритма противодавления. Для простоты сценарий, в котором события независимы и одинаковырассматривается распределение (iid) по слотам, хотя можно показать, что тот же алгоритм работает и в сценариях, отличных от iid (см.ниже в разделе «Работа без iid и универсальное планирование» ).

Динамичные поступления

Позволять $(A_{n}^{(c)}(t))$ быть матрицей экзогенных поступлений в слот t . Предположим, что эта матрица независима и тождественнараспределено (iid) по слотам с конечными вторыми моментами и со средствами:

$\lambda _{n}^{(c)}=E\left[A_{n}^{(c)}(t)\right]$

Предполагается, что $\lambda _{c}^{(c)}=0$ для всех $c\in \{1,\ldots ,N\}$, поскольку никакие данные, предназначенные для себя, не поступают. Таким образом,матрица скоростей прибытия $(\lambda _{n}^{(c)})$ это $N\times N$ матрица неотрицательных действительных чисел с нулями на диагонали.

Регион пропускной способности сети

Предположим, что состояние топологии S ( t ) является iid над слотами с вероятностями $\pi _{S}=Pr[S(t)=S]$(если S ( t ) принимает значения в несчетном бесконечном наборе векторов с вещественными элементами,затем $\pi _{S}$ представляет собой распределение вероятностей, а не функцию вероятностной массы).Общий алгоритм сети наблюдает S ( t ) в каждом слоте t и выбирает скорость передачи. $(\mu _{ab}(t))$ и переменные маршрутизации $(\mu _{ab}^{(c)}(t))$ в соответствии с ограничениями в уравнениях. (3)-(5). Область пропускной способности сети $\Lambda$ - это замыкание набора всех матриц скорости поступления $(\lambda _{n}^{(c)})$ для которого существует алгоритм, стабилизирующий сеть. Стабильность всех очередей подразумевает, что общая скорость ввода трафика в сеть такая же, как и общая скорость доставки данных по назначению. Можно показать, что для любой матрицы скорости поступления $(\lambda _{n}^{(c)})$ в области мощности $\Lambda$, существует стационарный и рандомизированный алгоритм , который выбирает переменные решения $(\mu _{ab}^{*}(t))$ и $(\mu _{ab}^{*(c)}(t))$каждый слот t на основе только S ( t ) (и, следовательно, независимо от невыполненных очередей)что дает следующее для всех $n\neq c$:

${\text{(Eq. 8)}}\qquad E\left[\lambda _{n}^{(c)}+\sum _{a=1}^{N}\mu _{an}^{*(c)}(t)-\sum _{b=1}^{N}\mu _{nb}^{*(c)}(t)\right]\leq 0$

Такой стационарный и рандомизированный алгоритм, который основывает решения только на S ( t ), называется только S-алгоритмом . Часто бывает полезно предположить, что $(\lambda _{n}^{(c)})$ является внутренним для $\Lambda$, так что существует $\epsilon >0$ такой, что $(\lambda _{n}^{(c)}+\epsilon 1_{n}^{(c)})\in \Lambda$, где $1_{n}^{(c)}$ равно 1, если $n\neq c$и ноль еще. В этом случае существует только S -алгоритм, который дает следующее для всех $n\neq c$:

${\text{(Eq. 9)}}\qquad E\left[\lambda _{n}^{(c)}+\sum _{a=1}^{N}\mu _{an}^{*(c)}(t)-\sum _{b=1}^{N}\mu _{nb}^{*(c)}(t)\right]\leq -\epsilon$

В качестве технического требования предполагается, что вторые моменты скоростей передачи $\mu _{ab}(t)$ конечны при любом алгоритме выбора этих скоростей. Это тривиально справедливо, если существует конечная максимальная скорость $\mu _{max}$.

Сравнение с алгоритмами только S

Поскольку алгоритм противодавления наблюдает ${\boldsymbol {Q}}(t)$ и S ( t ) каждый слот t и выбирает решения $(\mu _{ab}(t))$ и $(\mu _{ab}^{(c)}(t))$ чтобы минимизировать правую часть границы дрейфа (уравнение). (7), имеем:

${\text{(Eq. 10)}}\qquad \Delta (t)\leq B+\sum _{n=1}^{N}\sum _{c=1}^{N}Q_{n}^{(c)}(t)E\left[\lambda _{n}^{(c)}(t)+\sum _{a=1}^{N}\mu _{an}^{*(c)}(t)-\sum _{b=1}^{N}\mu _{nb}^{*(c)}(t)|{\boldsymbol {Q}}(t)\right]$

где $(\mu _{ab}^{*}(t))$ и $(\mu _{ab}^{*(c)}(t))$любые альтернативные решения, удовлетворяющие уравнениям. (3)-(5), включая рандомизированные решения.

Теперь предположим $(\lambda _{n}^{(c)})\in \Lambda$. Тогда существует S -только алгоритм, который удовлетворяет условиюуравнение (8). Подставив это в правую часть уравнения. (10) и отмечая, что условное математическое ожидание при условии ${\boldsymbol {Q}}(t)$ при этом алгоритме только S то же самое, что и безусловное ожидание (поскольку S ( t ) является iid для слотов, а алгоритм только S не зависит от текущих невыполненных очередей) дает:

$\Delta (t)\leq B\,$

Таким образом, дрейф квадратичной функции Ляпунова меньше или равен константе B для всех слотов t . Этот факт вместе с предположением о том, что поступления в очередь имеют ограниченные вторые моменты, подразумевают следующее для всех сетевых очередей:

$\lim _{t\rightarrow \infty }{\frac {Q_{n}^{(c)}(t)}{t}}=0{\text{ with probability 1}}$

Для более глубокого понимания среднего размера очереди можно предположить, что скорость поступления $(\lambda _{n}^{(c)})$ являются внутренними для $\Lambda$, так что есть $\epsilon >0$ такой, что уравнение (9) справедливо для некоторой альтернативы S -только алгоритм. Уравнение подключения (9) в правую часть уравнения. (10) дает:

$\Delta (t)\leq B-\epsilon \sum _{n=1}^{N}\sum _{c=1}^{N}Q_{n}^{(c)}(t)$

откуда сразу получается (см. ):

$\limsup _{t\rightarrow \infty }{\frac {1}{t}}\sum _{\tau =0}^{t-1}\sum _{n=1}^{N}\sum _{c=1}^{N}E\left[Q_{n}^{(c)}(\tau )\right]\leq {\frac {B}{\epsilon }}$

Эта граница среднего размера очереди увеличивается по мере увеличения расстояния. $\epsilon$ до границы г.регион мощности $\Lambda$ уходит в ноль. Это такая же качественная производительность, как и у одиночной очереди M/M/1 со скоростью поступления $\lambda$ и стоимость услуги $\mu$, гдесредний размер очереди пропорционален $1/\epsilon$, где $\epsilon =\mu -\lambda$.

Расширения приведенной выше формулировки

Не-iid операция и универсальное планирование

Приведенный выше анализ для простоты предполагает свойства iid. Однако можно показать, что тот же алгоритм противодавления надежно работает и в ситуациях, отличных от IID. Когда процессы прибытия и состояния топологии эргодичны, но не обязательно являются нейтральными, противодавление по-прежнему стабилизирует систему всякий раз, когда $(\lambda _{n}^{(c)})\in \Lambda$. В более общем плане было показано, что использование универсального подхода к планированию обеспечивает свойства стабильности и оптимальности для произвольных (возможно, неэргодических) путей выборки.

Противодавление с оптимизацией коммунальных услуг и минимизацией штрафов

Было показано, что противодавление работает в сочетании с контролем потока с помощью метода «дрейф плюс штраф» . Этот метод жадно максимизирует сумму дрейфа и выражение взвешенного штрафа. Наказание взвешивается параметром V , который определяет компромисс в производительности.Этот метод гарантирует, что полезность пропускной способности находится в пределах O (1/ V ) от оптимальности, а средняя задержка составляет O ( V ). Таким образом, полезность можно сколь угодно близко приблизить к оптимальности с соответствующим компромиссом в средней задержке. Аналогичные свойства могут быть продемонстрированы для минимизации средней мощности. и для оптимизации более общих сетевых атрибутов.

Разработаны альтернативные алгоритмы стабилизации очередей при максимальном использовании сетевой полезности.использование анализа модели жидкости, анализ суставной жидкости и анализ множителей Лагранжа, выпуклая оптимизация, и стохастические градиенты. Эти подходы не дают O (1/ V ), O ( V результатов задержки полезности ).

См. также

• АОДВ
• Разнесенная маршрутизация противодавления (DIVBAR)
• Дрифт плюс штраф
• ЭксОР
• Географическая маршрутизация
• Список протоколов специальной маршрутизации
• оптимизация Ляпунова

Первоисточники

• Л. Тассиулас и А. Эфремидес, «Свойства стабильности систем массового обслуживания с ограничениями и политики планирования для максимальной пропускной способности в многоскачковых радиосетях», Транзакции IEEE по автоматическому управлению , том. 37, нет. 12, стр. 1936–1948, декабрь 1992 г.
• Л. Георгиадис, М. Дж. Нили и Л. Тассиулас, «Распределение ресурсов и межуровневое управление в беспроводных сетях», « Основы и тенденции в области сетевых технологий » , том. 1, нет. 1, стр. 1–149, 2006.
• М. Дж. Нили. Стохастическая оптимизация сети с применением к системам связи и массового обслуживания , Morgan & Claypool, 2010.