Колорирование

Раскраска в 3 цвета (левый верхний рисунок): правильная 3-раскраска этого графа невозможна. Синий подграф образует клику графа (нижний правый рисунок), а красный и зеленый подграфы образуют клики в дополнении .

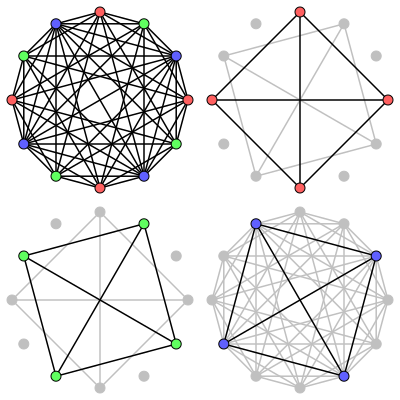
В теории графов раскраска — это графа G присвоение цветов вершинам так, что каждый цветовой класс образует множество в G или в дополнении к G. независимое Кохроматическое число z( G ) графа G — это наименьшее количество цветов, необходимых для любых G. раскрасок Графы с кохроматическим числом 2 — это в точности двудольные графы , дополнения к двудольным графам и расщепленные графы .

Поскольку требование того, чтобы каждый цветовой класс был кликой или независимым, слабее, чем требование для раскраски (в которой каждый цветовой класс должен быть независимым набором) и сильнее, чем для подраскраски (в которой каждый цветовой класс должен быть непересекающимся объединением клик) что кохроматическое число G меньше или равно хроматическому числу G и что оно больше или равно субхроматическому числу G. , отсюда следует ,

Колоринг был назван и впервые изучен Лесняком и Стрейтом (1977) . Йоргенсен (1995) характеризует критические 3-кохроматические графы, а Фомин, Крач и Новелли (2002) описывают алгоритмы аппроксимации кохроматического числа графа. Зверович (2000) определяет класс совершенных кохроматических графов , аналогичный определению совершенных графов посредством раскраски графов, и дает характеристику этих графов запрещенными подграфами.

Ссылки

• Фомин Федор Владимирович; Крач, Дитер; Новелли, Жан-Кристоф (2002), «Приближение минимальных раскрасок», Inf. Процесс. Летт. , 84 (5): 285–290, doi : 10.1016/S0020-0190(02)00288-0 , S2CID   17733740 .
• Гимбел, Джон; Стрейт, Х. Джозеф (1987), «Некоторые темы кохроматической теории», Graphs and Combinatorics , 3 (1): 255–265, doi : 10.1007/BF01788548 , S2CID   8218390 .
• Йоргенсен, Лейф К. (1995), «Критические 3-кохроматические графы», Graphs and Combinatorics , 11 (3): 263–266, doi : 10.1007/BF01793013 , S2CID   38851896 .
• Лесняк, Л.; Страйт, HJ (1977), «Кохроматическое число графа», Ars Combinatoria , 3 : 39–46 .
• Стрейт, Х.Дж. (1979), «Кохроматическое число и род графа», Журнал теории графов , 3 (1): 43–51, doi : 10.1002/jgt.3190030106 .
• Зверович, Игорь В. (2000), Совершенные кохроматические графы , Отчет об исследовании RRR 16-2000, Центр исследования операций Университета Рутгерса, заархивировано из оригинала 03 марта 2016 г. , получено 16 октября 2006 г.