Левая рекурсия

В теории языка информатики , формальной левая рекурсия — это частный случай рекурсии когда строка распознается как часть языка на основании того факта, что она разлагается на строку того же языка (слева) и суффикс (слева). право). Например, $1+2+3$ можно признать суммой, поскольку ее можно разбить на $1+2$ , также сумма, и ${}+3$ , подходящий суффикс.

С точки зрения контекстно-свободной грамматики , нетерминал является леворекурсивным, если крайний левый символ в одном из его произведений является самим собой (в случае прямой левой рекурсии) или может быть создан некоторой последовательностью подстановок (в случае косвенной грамматики). левая рекурсия).

Определение

Грамматика является леворекурсивной тогда и только тогда, когда существует нетерминальный символ. $A$ который может привести к форме предложения , где он будет самым левым символом. ^[1] Символически,

A\Rightarrow ^{+}A\alpha

,

где $\Rightarrow ^{+}$ указывает операцию выполнения одной или нескольких замен, и $\alpha$ — любая последовательность терминальных и нетерминальных символов.

Прямая левая рекурсия

Прямая левая рекурсия возникает, когда определение может быть удовлетворено только одной заменой. Требуется правило вида

A\to A\alpha

где $\alpha$ представляет собой последовательность нетерминалов и терминалов. Например, правило

{\mathit {Expression}}\to {\mathit {Expression}}+{\mathit {Term}}

является непосредственно леворекурсивным. слева направо Анализатор рекурсивного спуска для этого правила может выглядеть так:

void Expression() {
  Expression();
  match('+');
  Term();
}

и такой код при выполнении впадет в бесконечную рекурсию.

Косвенная левая рекурсия

Косвенная левая рекурсия возникает, когда определение левой рекурсии удовлетворяется посредством нескольких замен. Это влечет за собой набор правил, следующих шаблону

A_{0}\to \beta _{0}A_{1}\alpha _{0}

A_{1}\to \beta _{1}A_{2}\alpha _{1}

\cdots

A_{n}\to \beta _{n}A_{0}\alpha _{n}

где $\beta _{0},\beta _{1},\ldots ,\beta _{n}$ представляют собой последовательности, каждая из которых может дать пустую строку , а $\alpha _{0},\alpha _{1},\ldots ,\alpha _{n}$ могут быть любые последовательности терминальных и нетерминальных символов. Обратите внимание, что эти последовательности могут быть пустыми. Вывод

A_{0}\Rightarrow \beta _{0}A_{1}\alpha _{0}\Rightarrow ^{+}A_{1}\alpha _{0}\Rightarrow \beta _{1}A_{2}\alpha _{1}\alpha _{0}\Rightarrow ^{+}\cdots \Rightarrow ^{+}A_{0}\alpha _{n}\dots \alpha _{1}\alpha _{0}

затем дает $A_{0}$ как крайний левый в его окончательной форме предложения.

Использование

Левая рекурсия обычно используется как идиома для создания левоассоциативных операций : выражение a+b-c-d+e оценивается как (((a+b)-c)-d)+e. В этом случае этот порядок вычислений может быть достигнут с помощью синтаксиса с помощью трех грамматических правил.

{\mathit {Expression}}\to {\mathit {Term}}

{\mathit {Expression}}\to {\mathit {Expression}}+{\mathit {Term}}

{\mathit {Expression}}\to {\mathit {Expression}}-{\mathit {Term}}

Они позволяют только анализировать ${\mathit {Expression}}$ a+b-c-d+e как состоящий из ${\mathit {Expression}}$ a+b-c-d и ${\mathit {Term}}$ e, где a+b-c-d в свою очередь состоит из ${\mathit {Expression}}$ a+b-c и ${\mathit {Term}}$ d, пока a+b-c состоит из ${\mathit {Expression}}$ a+b и ${\mathit {Term}}$ c, и т. д.

Удаление левой рекурсии

Левая рекурсия часто создает проблемы для парсеров, либо потому, что она приводит их к бесконечной рекурсии (как в случае большинства нисходящих парсеров ), либо потому, что они ожидают правил в нормальной форме, которые запрещают это (как в случае многих восходящих парсеров). парсеры ^{[ нужны разъяснения ]}). Поэтому грамматика часто подвергается предварительной обработке для устранения левой рекурсии.

Удаление прямой левой рекурсии

Общий алгоритм удаления прямой левой рекурсии следующий. В этот метод было внесено несколько усовершенствований. ^[2] Для леворекурсивного нетерминала $A$ , отбросьте все правила вида $A\rightarrow A$ и рассмотрим те, что остались:

A\rightarrow A\alpha _{1}\mid \ldots \mid A\alpha _{n}\mid \beta _{1}\mid \ldots \mid \beta _{m}

где:

каждый $\alpha$ представляет собой непустую последовательность нетерминалов и терминалов, и
каждый $\beta$ представляет собой последовательность нетерминалов и терминалов, которая не начинается с $A$ .

Замените их двумя наборами произведений, один набор для $A$ :

A\rightarrow \beta _{1}A^{\prime }\mid \ldots \mid \beta _{m}A^{\prime }

и еще набор для свежего нетерминала $A'$ (часто называемый «хвостом» или «остатком»):

A^{\prime }\rightarrow \alpha _{1}A^{\prime }\mid \ldots \mid \alpha _{n}A^{\prime }\mid \epsilon

Повторяйте этот процесс до тех пор, пока не останется прямой левой рекурсии.

В качестве примера рассмотрим набор правил

{\mathit {Expression}}\rightarrow {\mathit {Expression}}+{\mathit {Expression}}\mid {\mathit {Integer}}\mid {\mathit {String}}

Это можно переписать, чтобы избежать левой рекурсии, как

{\mathit {Expression}}\rightarrow {\mathit {Integer}}\,{\mathit {Expression}}'\mid {\mathit {String}}\,{\mathit {Expression}}'

{\mathit {Expression}}'\rightarrow {}+{\mathit {Expression}}\,{\mathit {Expression}}'\mid \epsilon

Удаление всей левой рекурсии

Вышеописанный процесс можно расширить, чтобы исключить всю левую рекурсию, сначала преобразуя косвенную левую рекурсию в прямую левую рекурсию на нетерминале с наибольшим номером в цикле.

Входные данные Грамматика: набор нетерминалов $A_{1},\ldots ,A_{n}$ и их продукция

Выходные данные Модифицированная грамматика, генерирующая тот же язык, но без левой рекурсии.

Для каждого нетерминала $A_{i}$ :
1. Повторяйте до тех пор, пока итерация не оставит грамматику неизменной:
  1. Для каждого правила $A_{i}\rightarrow \alpha _{i}$ , $\alpha _{i}$ представляет собой последовательность терминалов и нетерминалов:
    1. Если $\alpha _{i}$ начинается с нетерминала $A_{j}$ и $j<i$ :
      1. Позволять $\beta _{i}$ быть $\alpha _{i}$ без его ведущего $A_{j}$ .
      2. Удалить правило $A_{i}\rightarrow \alpha _{i}$ .
      3. Для каждого правила $A_{j}\rightarrow \alpha _{j}$ :
        Добавить правило $A_{i}\rightarrow \alpha _{j}\beta _{i}$ .
2. Удалить прямую левую рекурсию для $A_{i}$ как описано выше.

Шаг 1.1.1 представляет собой расширение исходного нетерминального $A_{j}$ в правой части некоторого правила $A_{i}\to A_{j}\beta$ , но только если $j<i$ . Если $A_{i}\to A_{j}\beta$ был одним шагом в цикле продукций, приводящим к левой рекурсии, то это сократило этот цикл на один шаг, но часто за счет увеличения количества правил.

Алгоритм можно рассматривать как установление топологического порядка на нетерминалах: после этого может быть только правило $A_{i}\to A_{j}\beta$ если $j>i$ . Обратите внимание, что этот алгоритм очень чувствителен к нетерминальному упорядочению; оптимизации часто фокусируются на правильном выборе этого порядка.

Подводные камни

Хотя приведенные выше преобразования сохраняют язык, созданный грамматикой, они могут изменить деревья синтаксического анализа , которые свидетельствуют о распознавании строк. При соответствующем учете переписывание деревьев может восстановить оригиналы, но если этот шаг пропустить, различия могут изменить семантику анализа.

Ассоциативность особенно уязвима; В новой грамматике левоассоциативные операторы обычно появляются в форме правоассоциативной структуры. Например, начиная с этой грамматики:

{\mathit {Expression}}\rightarrow {\mathit {Expression}}\,-\,{\mathit {Term}}\mid {\mathit {Term}}

{\mathit {Term}}\rightarrow {\mathit {Term}}\,*\,{\mathit {Factor}}\mid {\mathit {Factor}}

{\mathit {Factor}}\rightarrow ({\mathit {Expression}})\mid {\mathit {Integer}}

стандартные преобразования для удаления левой рекурсии дают следующее:

{\mathit {Expression}}\rightarrow {\mathit {Term}}\ {\mathit {Expression}}'

{\mathit {Expression}}'\rightarrow {}-{\mathit {Term}}\ {\mathit {Expression}}'\mid \epsilon

{\mathit {Term}}\rightarrow {\mathit {Factor}}\ {\mathit {Term}}'

{\mathit {Term}}'\rightarrow {}*{\mathit {Factor}}\ {\mathit {Term}}'\mid \epsilon

{\mathit {Factor}}\rightarrow ({\mathit {Expression}})\mid {\mathit {Integer}}

Разбор строки «1 — 2 — 3» с помощью первой грамматики в анализаторе LALR (который может обрабатывать леворекурсивные грамматики) привел бы к получению дерева разбора:

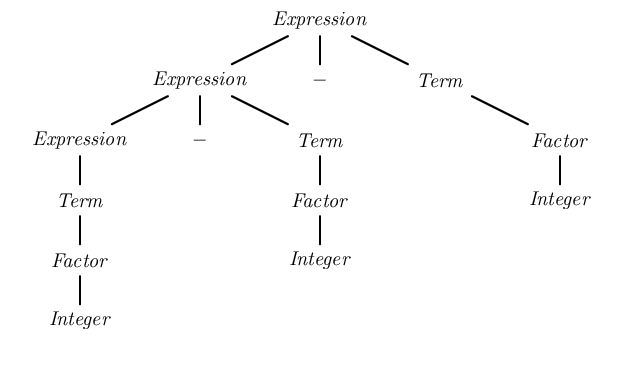
Леворекурсивный анализ двойного вычитания — Left-recursive parsing of a double subtraction

Это дерево разбора группирует термины слева, давая правильную семантику (1 - 2) - 3 .

Разбор со второй грамматикой дает

Праворекурсивный разбор двойного вычитания — Right-recursive parsing of a double subtraction

что при правильной интерпретации означает 1 + (-2 + (-3)) , что также правильно, но менее точно соответствует входным данным и гораздо сложнее реализовать для некоторых операторов. Обратите внимание, как члены справа появляются глубже в дереве, подобно тому, как праворекурсивная грамматика расположила бы их для 1 - (2 - 3) .

Учет левой рекурсии при синтаксическом анализе сверху вниз

, Формальная грамматика содержащая левую рекурсию, не может быть проанализирована LL (k)-анализатором или другим анализатором наивного рекурсивного спуска , если она не преобразована в слабо эквивалентную праворекурсивную форму. Напротив, левая рекурсия предпочтительнее для анализаторов LALR , поскольку она приводит к меньшему использованию стека, чем правая рекурсия . Однако более сложные нисходящие синтаксические анализаторы могут реализовать общие контекстно-свободные грамматики за счет сокращения. В 2006 году Фрост и Хафиз описали алгоритм, который учитывает неоднозначные грамматики с помощью прямых леворекурсивных правил производства . ^[3] Этот алгоритм был расширен до полного алгоритма синтаксического анализа , чтобы обеспечить как косвенную, так и прямую левую рекурсию за полиномиальное время, а также генерировать компактные представления полиномиального размера потенциально экспоненциального числа деревьев синтаксического анализа для весьма неоднозначных грамматик Фростом, Хафизом и Каллаганом в 2007 году. . ^[4] Затем авторы реализовали алгоритм в виде набора комбинаторов парсеров, написанных на языке программирования Haskell . ^[5]

См. также

Хвостовая рекурсия

Ссылки

^ Заметки по теории формального языка и синтаксическому анализу в Wayback Machine (архивировано 27 ноября 2007 г.). Джеймс Пауэр, факультет компьютерных наук Национального университета Ирландии, Мейнут Мейнут, графство Килдэр, Ирландия. JPR02
^ Мур, Роберт К. (май 2000 г.). «Удаление левой рекурсии из контекстно-свободных грамматик» (PDF) . 6-я конференция по прикладной обработке естественного языка : 249–255.
^ Фрост, Р.; Р. Хафиз (2006). «Новый алгоритм синтаксического анализа сверху вниз для устранения неоднозначности и левой рекурсии за полиномиальное время» . Уведомления ACM SIGPLAN . 41 (5): 46–54. дои : 10.1145/1149982.1149988 . S2CID 8006549 . , доступно у автора по адресу http://hafiz.myweb.cs.uwindsor.ca/pub/p46-frost.pdf. Архивировано 8 января 2015 г. на Wayback Machine.
^ Фрост, Р.; Р. Хафиз; П. Каллаган (июнь 2007 г.). «Модульный и эффективный нисходящий анализ неоднозначных леворекурсивных грамматик» (PDF) . 10-й международный семинар по технологиям синтаксического анализа (IWPT), ACL-SIGPARSE : 109–120. Архивировано из оригинала (PDF) 27 мая 2011 г.
^ Фрост, Р.; Р. Хафиз; П. Каллаган (январь 2008 г.). «Парсер-комбинаторы неоднозначных леворекурсивных грамматик». Практические аспекты декларативных языков (PDF) . Конспекты лекций по информатике. Том. 4902. стр. 167–181. дои : 10.1007/978-3-540-77442-6_12 . ISBN 978-3-540-77441-9 .

Внешние ссылки

Практические соображения по грамматике LALR(1)

[1] Заметки по теории формального языка и синтаксическому анализу в Wayback Machine (архивировано 27 ноября 2007 г.). Джеймс Пауэр, факультет компьютерных наук Национального университета Ирландии, Мейнут Мейнут, графство Килдэр, Ирландия. JPR02

[Moore2000-2] Мур, Роберт К. (май 2000 г.). «Удаление левой рекурсии из контекстно-свободных грамматик» (PDF) . 6-я конференция по прикладной обработке естественного языка : 249–255.

[FrostHafiz2006-3] Фрост, Р.; Р. Хафиз (2006). «Новый алгоритм синтаксического анализа сверху вниз для устранения неоднозначности и левой рекурсии за полиномиальное время» . Уведомления ACM SIGPLAN . 41 (5): 46–54. дои : 10.1145/1149982.1149988 . S2CID 8006549 . , доступно у автора по адресу http://hafiz.myweb.cs.uwindsor.ca/pub/p46-frost.pdf. Архивировано 8 января 2015 г. на Wayback Machine.

[FrostHafizCallaghan2007-4] Фрост, Р.; Р. Хафиз; П. Каллаган (июнь 2007 г.). «Модульный и эффективный нисходящий анализ неоднозначных леворекурсивных грамматик» (PDF) . 10-й международный семинар по технологиям синтаксического анализа (IWPT), ACL-SIGPARSE : 109–120. Архивировано из оригинала (PDF) 27 мая 2011 г.

[FrostHafizCallaghan2008-5] Фрост, Р.; Р. Хафиз; П. Каллаган (январь 2008 г.). «Парсер-комбинаторы неоднозначных леворекурсивных грамматик». Практические аспекты декларативных языков (PDF) . Конспекты лекций по информатике. Том. 4902. стр. 167–181. дои : 10.1007/978-3-540-77442-6_12 . ISBN 978-3-540-77441-9 .

[1]

[2]

[3]

[4]

[5]