Алгоритм Укконена

В информатике построения алгоритм Укконена с линейным временем — это онлайн-алгоритм суффиксных деревьев , предложенный Эско Укконеном в 1995 году. ^{[ 1 ]} Алгоритм начинается с неявного суффиксного дерева, содержащего первый символ строки. Затем он проходит по строке, добавляя последовательные символы, пока дерево не будет завершено. Такой порядок сложения символов придает алгоритму Укконена свойство «онлайн». Оригинальный алгоритм, представленный Питером Вайнером, действовал в обратном порядке от последнего символа к первому, от самого короткого к самому длинному суффиксу. ^{[ 2 ]} Более простой алгоритм был найден Эдвардом М. МакКрайтом , идущим от самого длинного суффикса к самому короткому. ^{[ 3 ]}

Неявное суффиксное дерево

При создании суффиксного дерева с использованием алгоритма Укконена мы увидим неявное суффиксное дерево на промежуточных шагах в зависимости от символов в строке S. В неявных суффиксных деревьях не будет ребра с меткой $ (или любого другого символа завершения) и внутреннего узла с только один край выходит из него.

Высокоуровневое описание алгоритма Укконена

Алгоритм Укконена строит неявное суффиксное дерево T _i для каждого префикса S[1...i] из S (S — строка длины n). Сначала он строит T _1, используя 1 ^ул. символ, затем T _2, используя 2 ^nd символ, затем T _3, используя 3 ^р-д символ, ..., T _n с использованием n ^й характер. В суффиксном дереве, использующем алгоритм Укконена, можно найти следующие характеристики:

Неявное суффиксное дерево Ti ₊₁ строится на основе неявного суффиксного дерева _Ti .
В любой момент времени алгоритм Укконена строит суффиксное дерево для уже увиденных символов, поэтому оно обладает свойством онлайн , что позволяет алгоритму иметь время выполнения O (n).
Алгоритм Укконена разделен на n этапов (по одному этапу на каждый символ строки длиной n).
Каждая фаза i+1 далее делится на i+1 расширений, по одному на каждый из i+1 суффиксов S[1...i+1].

Расширение суффикса заключается в добавлении следующего символа в построенное на данный момент дерево суффиксов. В расширении j фазы i+1 алгоритм находит конец S[j...i] (который уже находится в дереве из-за предыдущей фазы i), а затем расширяет S[j...i], чтобы быть уверенным. суффикс S[j...i+1] находится в дереве. Существует три правила расширения:

Если путь от корня с меткой S[j...i] заканчивается на краю листа (т. е. S[i] является последним символом на краю листа), то символ S[i+1] просто добавляется в конец этикетка на краю листа.
если путь от корня с меткой S[j...i] заканчивается на нелистовом ребре (т. е. после S[i] в пути есть еще символы) и следующий символ не S[i+1], то создается новое ребро листа с меткой S[i+1] и номером j, начиная с символа S[i+1]. Новый внутренний узел также будет создан, если S[1...i] заканчивается внутри (между) нелистового ребра.
Если путь от корня с меткой S[j..i] заканчивается на нелистовом ребре (т. е. после S[i] в пути есть еще символы) и следующим символом является S[i+1] (уже в дереве ), ничего не делать.

Следует отметить один важный момент: от данного узла (корневого или внутреннего) будет одно и только одно ребро, начинающееся с одного символа. Из любого узла, начинающегося с одного и того же символа, не будет выходить более одного ребра.

Время выполнения

Простая реализация для создания суффиксного дерева в дальнейшем требует $O (n 2)$ или даже $O (n 3)$ временная сложность в big O нотации , где $n$ — длина строки. Используя ряд алгоритмических методов, Укконен сократил это время до $O (n)$ (линейного) для алфавитов постоянного размера и до $O (n log n)$ в целом, что соответствует производительности во время выполнения двух предыдущих алгоритмов.

Пример алгоритма Укконена

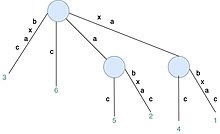
Чтобы лучше проиллюстрировать, как строится суффиксное дерево с использованием алгоритма Укконена, мы можем рассмотреть строку S = xabxac.

Начните с пустого корневого узла.
Построить $T_{1}$ для S[1] добавив первый символ строки. Применяется правило 2, которое создает новый листовой узел.
Построить $T_{2}$ для S[1..2] путем добавления суффиксов xa ( xa и a). Применяется правило 1, которое расширяет метку пути на существующем краю листа. Применяется правило 2, которое создает новый листовой узел.
Построить $T_{3}$ для S[1..3] путем добавления суффиксов xab ( xab, ab и b). Применяется правило 1, которое расширяет метку пути на существующем краю листа. Применяется правило 2, которое создает новый листовой узел.
Построить $T_{4}$ для S[1..4] путем добавления суффиксов xabx ( xabx, abx, bx и x). Применяется правило 1, которое расширяет метку пути на существующем краю листа. Применяется правило 3: ничего не делайте.
Конструкции $T_{5}$ для S[1..5] путем добавления суффиксов xabxa ( xabxa, abxa, bxa, xa и a). Применяется правило 1, которое расширяет метку пути на существующем краю листа. Применяется правило 3: ничего не делайте.
Конструкции $T_{6}$ для S[1..6] путем добавления суффиксов xabxac ( xabxac, abxac, bxac, xac, ac и c). Применяется правило 1, которое расширяет метку пути на существующем краю листа. Применяется правило 2, которое создает новый листовой узел (в этом случае создаются три новых ребра листа и два новых внутренних узла).

Ссылки

^ Укконен, Э. (1995). «Онлайн-построение суффиксных деревьев» (PDF) . Алгоритмика . 14 (3): 249–260. CiteSeerX 10.1.1.10.751 . дои : 10.1007/BF01206331 . S2CID 6027556 .
^ Вайнер, Питер (1973). «Алгоритмы сопоставления линейных образцов» (PDF) . 14-й ежегодный симпозиум по теории коммутации и автоматов (SWAT 1973) . стр. 1–11. CiteSeerX 10.1.1.474.9582 . дои : 10.1109/SWAT.1973.13 .
^ МакКрайт, Эдвард Мейерс (1976). «Алгоритм построения суффиксного дерева с экономикой пространства». Журнал АКМ . 23 (2): 262–272. CiteSeerX 10.1.1.130.8022 . дои : 10.1145/321941.321946 . S2CID 9250303 .

Внешние ссылки

Подробное объяснение на простом английском языке
Быстрый поиск строк с помощью суффиксных деревьев . Учебное пособие Марка Нельсона. Имеет пример реализации, написанный на C++.
Реализация на C с подробным объяснением
Слайды лекций Гая Блеллоха
Домашняя страница Укконена
Проект индексирования текста (построение суффиксных деревьев Укконеном за линейное время)
Реализация на C Часть 1 Часть 2 Часть 3 Часть 4 Часть 5 Часть 6

Эта алгоритмам или структурам данных, статья, посвященная является незавершенной . Вы можете помочь Википедии, расширив ее .

[1] Укконен, Э. (1995). «Онлайн-построение суффиксных деревьев» (PDF) . Алгоритмика . 14 (3): 249–260. CiteSeerX 10.1.1.10.751 . дои : 10.1007/BF01206331 . S2CID 6027556 .

[2] Вайнер, Питер (1973). «Алгоритмы сопоставления линейных образцов» (PDF) . 14-й ежегодный симпозиум по теории коммутации и автоматов (SWAT 1973) . стр. 1–11. CiteSeerX 10.1.1.474.9582 . дои : 10.1109/SWAT.1973.13 .

[3] МакКрайт, Эдвард Мейерс (1976). «Алгоритм построения суффиксного дерева с экономикой пространства». Журнал АКМ . 23 (2): 262–272. CiteSeerX 10.1.1.130.8022 . дои : 10.1145/321941.321946 . S2CID 9250303 .

[ 1 ]

[ 2 ]

[ 3 ]