прыжки на спине

В обратного отслеживания алгоритмах обратный прыжок — это метод, который уменьшает пространство поиска , тем самым повышая эффективность. Хотя возврат всегда поднимается на один уровень вверх в дереве поиска , когда все значения переменной проверены, обратный переход может подниматься на несколько уровней выше. В этой статье фиксированный порядок оценки переменных $x_{1},\ldots ,x_{n}$ используется, но те же соображения применимы и к динамическому порядку оценки.

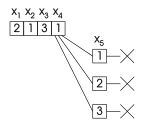
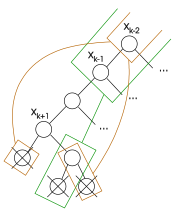
Дерево поиска, посещаемое при обычном возврате
Обратный прыжок: серый узел не посещается

Определение

Всякий раз, когда при возврате перепробованы все значения переменной и не найдено никакого решения, он пересматривает последнюю из ранее присвоенных переменных, изменяя ее значение или совершая дальнейший возврат, если другие значения не должны быть проверены. Если $x_{1}=a_{1},\ldots ,x_{k}=a_{k}$ — текущее частичное присвоение и все значения для $x_{k+1}$ были опробованы, но не нашли решения, возврат к выводу, что ни одно решение не расширяет $x_{1}=a_{1},\ldots ,x_{k}=a_{k}$ существует. Затем алгоритм «поднимается» к $x_{k}$ , изменение $x_{k}$ значение, если возможно, в противном случае снова возвращаемся.

Частичное присвоение не всегда необходимо в полном объеме, чтобы доказать отсутствие значения $x_{k+1}$ приводит к решению. В частности, таким же свойством может обладать префикс частичного присваивания, то есть существовать индекс $j<k$ такой, что $x_{1},\ldots ,x_{j}=a_{1},\ldots ,a_{j}$ не может быть расширено для формирования решения с каким бы то ни было значением $x_{k+1}$ . Если алгоритм сможет доказать этот факт, он сможет напрямую рассмотреть другое значение для $x_{j}$ вместо того, чтобы пересмотреть $x_{k}$ как это обычно бывает.


Пример, в котором текущее присвоение $x_{1}x_{2}x_{3}x_{4}$ был безуспешно опробован со всеми возможными значениями $x_{5}$ . Возврат возвращается к $x_{4}$ , пытаясь присвоить ему новое значение.	Вместо возврата алгоритм делает дальнейшую разработку, доказывая, что оценки $x_{1}x_{2}x_{5}=211$ , $x_{1}x_{2}x_{5}=212$ , и $x_{1}x_{2}x_{5}=213$ не являются частью какого-либо решения.	В результате текущая оценка $x_{1}x_{2}$ не является частью какого-либо решения, и алгоритм может напрямую вернуться к $x_{2}$ , пробуя для него новое значение.

Эффективность алгоритма обратного прыжка зависит от того, насколько высоко он способен совершить обратный прыжок. В идеале алгоритм мог бы перейти от $x_{k+1}$ к любой переменной $x_{j}$ такова, что текущее присвоение $x_{1},\ldots ,x_{j}$ не может быть продолжено для получения решения с любым значением $x_{k+1}$ . Если это так, $j$ называется безопасным прыжком .

Установить, безопасен ли переход, не всегда возможно, поскольку безопасные переходы определяются с точки зрения набора решений, который и пытается найти алгоритм. На практике алгоритмы обратного прыжка используют наименьший индекс, который они могут эффективно доказать как безопасный прыжок. Разные алгоритмы используют разные методы определения безопасности прыжка. Эти методы имеют разную стоимость, но более высокая стоимость поиска более высокого безопасного прыжка может быть компенсирована сокращением объема поиска из-за пропуска частей дерева поиска.

Обратный прыжок на листовых узлах

Простейшее условие, при котором возможен обратный прыжок, — это когда все значения переменной оказались несовместимыми без дальнейшего ветвления. При удовлетворении ограничений частичная оценка непротиворечива тогда и только тогда, когда она удовлетворяет всем ограничениям, включающим назначенные переменные, и несовместима в противном случае. Может случиться так, что непротиворечивое частичное решение не может быть расширено до непротиворечивого полного решения, поскольку некоторые из неназначенных переменных не могут быть присвоены без нарушения других ограничений.

Состояние, при котором все значения данной переменной $x_{k+1}$ несовместимы с текущим частичным решением $x_{1},\ldots ,x_{k}=a_{1},\ldots ,a_{k}$ называется листовым тупиком . Это происходит именно тогда, когда переменная $x_{k+1}$ является листом дерева поиска (который соответствует узлам, имеющим только дочерние листья на рисунках этой статьи).

Алгоритм обратного прыжка Джона Гашнига выполняет обратный прыжок только в тупиках листьев. Другими словами, он работает иначе, чем возврат назад, только когда каждое возможное значение $x_{k+1}$ было протестировано и оказалось противоречивым без необходимости ветвления по другой переменной.

Безопасный прыжок можно найти, просто вычислив для каждого значения $a_{k+1}$ , самый короткий префикс $x_{1},\ldots ,x_{k}=a_{1},\ldots ,a_{k}$ несовместимый с $x_{k+1}=a_{k+1}$ . Другими словами, если $a_{k+1}$ это возможное значение для $x_{k+1}$ , алгоритм проверяет согласованность следующих оценок:

$x_{1}=a_{1}$	...	$x_{k-1}=a_{k-1}$	$x_{k}=a_{k}$	$x_{k+1}=a_{k+1}$
$x_{1}=a_{1}$	...	$x_{k-1}=a_{k-1}$		$x_{k+1}=a_{k+1}$
...
$x_{1}=a_{1}$				$x_{k+1}=a_{k+1}$

Наименьший индекс (самый нижний в списке), для которого оценки противоречивы, будет безопасным скачком, если $x_{k+1}=a_{k+1}$ были единственной возможной ценностью для $x_{k+1}$ . Поскольку каждая переменная обычно может принимать более одного значения, максимальный индекс, который получается в результате проверки для каждого значения, представляет собой безопасный переход и является точкой перехода алгоритма Джона Гашнига.

На практике алгоритм может проверять приведенные выше оценки одновременно с проверкой согласованности $x_{k+1}=a_{k+1}$ .

Прыжки назад во внутренних узлах

Предыдущий алгоритм выполняет обратный переход только тогда, когда значения переменной могут оказаться несовместимыми с текущим частичным решением без дальнейшего ветвления. Другими словами, он допускает обратный переход только на конечных узлах дерева поиска.

Внутренний узел дерева поиска представляет собой присвоение переменной, согласованной с предыдущими. Если ни одно решение не расширяет это назначение, предыдущий алгоритм всегда возвращается назад: в этом случае обратный прыжок не выполняется.

Обратный переход на внутренних узлах не может быть выполнен, как на листовых узлах. Действительно, если некоторые оценки $x_{k+1}$ требуется ветвление, потому что они соответствуют текущему назначению. В результате поиск префикса, не соответствующего этим значениям последней переменной, не увенчается успехом.

В таких случаях, что доказала оценка $x_{k+1}=a_{k+1}$ не быть частью решения с текущей частичной оценкой $x_{1},\ldots ,x_{k}$ это рекурсивный поиск. В частности, алгоритм «знает», что с этого момента решения не существует, поскольку он возвращается к этому узлу вместо того, чтобы остановиться после нахождения решения.

Этот возврат обусловлен рядом тупиков , точек, в которых алгоритм доказал несовместимость частичного решения. Для дальнейшего обратного прыжка алгоритм должен учитывать, что невозможность нахождения решения связана с этими тупиками. В частности, безопасные переходы — это индексы префиксов, которые по-прежнему делают эти тупики несовместимыми частичными решениями.


В этом примере алгоритм возвращается к $x_{k+1}$ , после перебора всех возможных значений из-за трех пересеченных точек несоответствия.	Второй пункт остается противоречивым, даже если значения $x_{k+1}$ и $x_{k}$ удаляются из частичной оценки (обратите внимание, что значения переменной находятся в ее дочерних элементах)	Остальные противоречивые оценки остаются таковыми даже без $x_{k-2}$ , $x_{k-1}$ , и $x_{k}$	Алгоритм может вернуться к $x_{k-2}$ поскольку это самые низкие переменные, которые сохраняют все несоответствия. Новое значение для $x_{k-2}$ будет судим.

Другими словами, когда все значения $x_{k+1}$ были опробованы, алгоритм может вернуться к предыдущей переменной $x_{i}$ при условии, что текущая оценка истинности $x_{1},\ldots ,x_{i}$ несовместимо со всеми истинными оценками $x_{k+1},x_{k+2},...$ в листовых узлах, которые являются потомками узла $x_{k+1}$ .

Упрощения

В поисках возможного прыжка назад для $x_{k+1}$ или одного из его предков, все узлы в заштрихованной области можно игнорировать.

Из-за потенциально большого количества узлов, находящихся в поддереве $x_{k+1}$ , информация, необходимая для безопасного прыжка назад с $x_{k+1}$ собирается во время посещения его поддерева. Поиск безопасного прыжка можно упростить с помощью двух соображений. Во-первых, алгоритму нужен безопасный прыжок, но он по-прежнему работает с прыжком, который не является максимально безопасным.

Второе упрощение заключается в том, что узлы поддерева $x_{l}$ которые были пропущены прыжком назад, можно игнорировать при поиске прыжка назад для $x_{l}$ . Точнее, все узлы, пропущенные обратным переходом от узла $x_{m}$ до узла $x_{l}$ не имеют отношения к поддереву с корнем в $x_{m}$ , а также не имеют значения другие их поддеревья.

Действительно, если алгоритм вышел из узла $x_{l}$ к $x_{m}$ по тропе, но совершает обратный прыжок на обратном пути, тогда он мог бы пойти прямо от $x_{l}$ к $x_{m}$ вместо. Действительно, обратный прыжок указывает на то, что узлы между $x_{l}$ и $x_{m}$ не имеют отношения к поддереву с корнем в $x_{m}$ . Другими словами, обратный переход указывает на то, что посещение области дерева поиска было ошибкой. Поэтому эту часть дерева поиска можно игнорировать при рассмотрении возможного обратного прыжка с $x_{l}$ или от одного из его предков.

Переменные, значений которых достаточно, чтобы доказать невыполнимость в поддереве с корнем в узле, собираются в узле и отправляются (после удаления переменной узла) в узел выше при отводе.

Этот факт можно использовать, собирая в каждом узле набор ранее назначенных переменных, оценки которых достаточно, чтобы доказать, что в поддереве с корнем в узле не существует решения. Этот набор создается в ходе выполнения алгоритма. При отводе от узла этот набор удаляется из переменной узла и собирается в набор пункта назначения обратного отслеживания или обратного перехода. Поскольку узлы, пропущенные при обратном прыжке, никогда не извлекаются, их наборы автоматически игнорируются.

Прыжки назад на основе графа

Смысл обратного прыжка на основе графа заключается в том, что безопасный прыжок можно найти, проверив, какая из переменных $x_{1},\ldots ,x_{k}$ находятся в ограничении с переменными $x_{k+1},x_{k+2},...$ которые создаются в конечных узлах. Для каждого листового узла и каждой переменной $x_{i}$ индекса $i>k$ который создается там, индексы меньше или равны $k$ чья переменная находится в ограничении с $x_{i}$ можно использовать для поиска безопасных прыжков. В частности, когда все значения для $x_{k+1}$ были опробованы, этот набор содержит индексы переменных, оценки которых позволяют доказать, что решение не может быть найдено путем посещения поддерева с корнем в $x_{k+1}$ . В результате алгоритм может вернуться к самому высокому индексу в этом наборе.

Тот факт, что узлы, пропущенные при обратном переходе, можно игнорировать при рассмотрении дальнейшего обратного перехода, можно использовать с помощью следующего алгоритма. При выходе из листового узла создается набор переменных, которые ограничены им, и «отправляется обратно» своему родителю или предку в случае обратного перехода. На каждом внутреннем узле поддерживается набор переменных. Каждый раз, когда набор переменных получен от одного из его дочерних элементов или потомков, их переменные добавляются к поддерживаемому набору. При дальнейшем возврате или обратном переходе из узла переменная узла удаляется из этого набора, и набор отправляется в узел, который является местом назначения обратного отслеживания или обратного перехода. Этот алгоритм работает, потому что набор, поддерживаемый в узле, собирает все переменные, необходимые для доказательства невыполнимости листьев, являющихся потомками этого узла. Поскольку наборы переменных передаются только при обратной трассировке от узлов, наборы, собранные в узлах, пропущенных при обратном переходе, автоматически игнорируются.

Прыжки на спине, основанные на конфликте (также известные как прыжки на спине, направленные на конфликт (cbj))

Еще более усовершенствованный алгоритм обратного перехода, иногда способный достигать больших обратных переходов, основан не только на проверке общего присутствия двух переменных в одном и том же ограничении, но также на проверке того, действительно ли ограничение вызвало несогласованность. В частности, этот алгоритм собирает одно из нарушенных ограничений на каждом листе. В каждом узле безопасным переходом является наивысший индекс переменной, находящейся в одном из ограничений, собранных на листьях.

Хотя выбранное в каждом листе нарушенное ограничение не влияет на безопасность результирующего прыжка, выбор ограничений с максимально возможными индексами увеличивает высоту прыжка. По этой причине ограничения на порядок обратного перехода на основе конфликтов, таким образом, ограничения на переменные с более низкими индексами являются более предпочтительными, чем ограничения на переменные с более высокими индексами.

Формально ограничение $C$ предпочтительнее другого $D$ если наивысший индекс переменной в $C$ но не в $D$ ниже, чем наивысший индекс переменной в $D$ но не в $C$ . Другими словами, за исключением общих переменных, предпочтение отдается ограничению, имеющему все нижние индексы.

В листовом узле алгоритм выбирает наименьший индекс $i$ такой, что $x_{1},\ldots ,x_{i}$ несовместимо с последней переменной, вычисленной в листе. Среди ограничений, нарушаемых при этой оценке, он выбирает наиболее предпочтительное и собирает все его показатели менее $k+1$ . Таким образом, когда алгоритм возвращается к переменной $x_{k+1}$ , наименьший полученный индекс идентифицирует безопасный прыжок.

На практике этот алгоритм упрощается за счет сбора всех индексов в один набор вместо создания набора для каждого значения $k$ . В частности, алгоритм собирает в каждом узле все наборы, поступающие от его потомков, которые не были пропущены при обратном прыжке. При отводе из этого узла этот набор удаляется из переменной узла и собирается в пункт назначения обратного отслеживания или обратного перехода.

Прыжки назад, направленные на конфликт, были предложены для решения задач удовлетворения ограничений Патриком Проссером в его основополагающей статье 1993 года.

См. также

Ссылки

Дектер, Рина (2003). Обработка ограничений . Морган Кауфманн. ISBN 1-55860-890-7 .
Проссер, Патрик (1993). «Гибридные алгоритмы для задачи удовлетворения ограничений» (PDF) . Вычислительный интеллект 9(3).