Основная теорема (анализ алгоритмов)

При анализе алгоритмов основная теорема для повторений по принципу «разделяй и властвуй» обеспечивает асимптотический анализ многих рекуррентных соотношений , которые встречаются при анализе алгоритмов «разделяй и властвуй» . Этот подход был впервые представлен Джоном Бентли , Доротеей Блостейн (урожденной Хакен) и Джеймсом Б. Саксом в 1980 году, где он был описан как «объединяющий метод» для решения таких повторений. ^[1] Название «основная теорема» было популяризировано широко используемым учебником по алгоритмам « в алгоритмы» Кормена Введение , Лейзерсона , Ривеста и Штейна .

Не все рекуррентные соотношения могут быть решены с помощью этой теоремы; к его обобщениям относится метод Акры–Бацци .

Введение [ править ]

Рассмотрим задачу, которую можно решить с помощью рекурсивного алгоритма, например следующего:

процедура  p(вход  x  размера  n  ): 
      если   n  < некоторая константа  k  : 
          Решите  x  напрямую без рекурсии 
      еще  : 
          Создайте  подзадачи  x  n  , каждая из которых имеет размер  /  b  . 
          Вызов процедуры  p  рекурсивно для каждой подзадачи 
          Объедините результаты подзадач

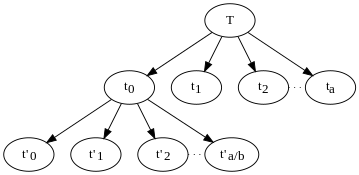
Приведенный выше алгоритм рекурсивно делит проблему на несколько подзадач, каждая из которых имеет размер $n / b$ . В его дереве решений есть узел для каждого рекурсивного вызова, а дочерними элементами этого узла являются другие вызовы, сделанные из этого вызова. Листья дерева — это базовые случаи рекурсии, подзадачи (размером меньше k ), которые не повторяются. будут $дочерние$ В приведенном выше примере в каждом неконечном узле узлы. Каждый узел выполняет объем работы, соответствующий размеру подзадачи $n,$ переданной этому экземпляру рекурсивного вызова и заданной выражением $f(n)$ . Общий объем работы, выполняемой всем алгоритмом, представляет собой сумму работы, выполненной всеми узлами дерева.

Время выполнения алгоритма, такого как $p$ выше, на входе размера $n$ , обычно обозначается $T(n)$ , может быть выражено рекуррентным соотношением

T(n)=a\;T\left({\frac {n}{b}}\right)+f(n),

где $f(n)$ настало время создать подзадачи и объединить их результаты в описанной выше процедуре. Это уравнение можно последовательно подставлять само в себя и расширять, чтобы получить выражение для общего объема проделанной работы. ^[2] Основная теорема позволяет преобразовать многие рекуррентные отношения этой формы в Θ-нотацию напрямую, без расширения рекурсивного отношения.

Общая форма [ править ]

Основная теорема всегда дает асимптотически точные границы повторений с помощью алгоритмов «разделяй и властвуй» , которые разбивают входные данные на более мелкие подзадачи одинакового размера, решают подзадачи рекурсивно, а затем объединяют решения подзадач, чтобы дать решение исходной проблемы. Время для такого алгоритма можно выразить путем сложения работы, которую они выполняют на верхнем уровне своей рекурсии (чтобы разделить проблемы на подзадачи и затем объединить решения подзадач), вместе со временем, затраченным на рекурсивные вызовы алгоритма. Если $T(n)$ обозначает общее время работы алгоритма на входе размером $n$ , и $f(n)$ обозначает количество времени, затраченное на верхнем уровне повторения, тогда время может быть выражено рекуррентным соотношением , которое принимает форму:

T(n)=a\;T\!\left({\frac {n}{b}}\right)+f(n)

Здесь $n$ размер входной проблемы, $a$ количество подзадач в рекурсии, а $b$ — коэффициент, на который уменьшается размер подзадачи при каждом рекурсивном вызове (b>1). Крайне важно, $a$ и $b$ не должно зависеть от $n$ . В приведенной ниже теореме также предполагается, что в качестве базового случая повторения $T(n)=\Theta (1)$ когда $n$ меньше некоторой границы $\kappa >0$ , наименьший входной размер, который приведет к рекурсивному вызову.

Повторения этой формы часто удовлетворяют одному из трех следующих режимов, в зависимости от того, как происходит разделение/восстановление проблемы. $f(n)$ относится к критическому показателю $c_{\operatorname {crit} }=\log _{b}a$ . (В таблице ниже используется стандартное обозначение «большая О» ).

c_{\operatorname {crit} }=\log _{b}a=\log(\#{\text{subproblems}})/\log({\text{relative subproblem size}})

Случай	Описание	Состояние включено $f(n)$ в связи с $c_{\operatorname {crit} }$ , то есть $\log _{b}a$	Основная теорема связана	Примеры обозначений
1	Работа по разделению/восстановлению проблемы затмевается подзадачами. т.е. дерево рекурсии многолистное	Когда $f(n)=O(n^{c})$ где $c<c_{\operatorname {crit} }$ (ограничен сверху полиномом меньшей степени)	... затем $T(n)=\Theta \left(n^{c_{\operatorname {crit} }}\right)$ (Термин расщепления не появляется; доминирует рекурсивная древовидная структура.)	Если $b=a^{2}$ и $f(n)=O(n^{1/2-\epsilon })$ , затем $T(n)=\Theta (n^{1/2})$ .
2	Работу по разделению/восстановлению проблемы можно сравнить с подзадачами.	Когда $f(n)=\Theta (n^{c_{\operatorname {crit} }}\log ^{k}n)$ для $k\geq 0$ (диапазон ограничен полиномом критической экспоненты, умноженным на ноль или более необязательно $\log$ с)	... затем $T(n)=\Theta \left(n^{c_{\operatorname {crit} }}\log ^{k+1}n\right)$ (Граница — это член разделения, при котором журнал увеличивается на одну степень.)	Если $b=a^{2}$ и $f(n)=\Theta (n^{1/2})$ , затем $T(n)=\Theta (n^{1/2}\log n)$ . Если $b=a^{2}$ и $f(n)=\Theta (n^{1/2}\log n)$ , затем $T(n)=\Theta (n^{1/2}\log ^{2}n)$ .
3	Работа по разделению/восстановлению проблемы доминирует над подзадачами. т.е. дерево рекурсии имеет много корней.	Когда $f(n)=\Omega (n^{c})$ где $c>c_{\operatorname {crit} }$ (ограничено снизу полиномом большей степени)	... это не обязательно что-нибудь даст. Кроме того, если $af\left({\frac {n}{b}}\right)\leq kf(n)$ для некоторой константы $k<1$ и все достаточно большие $n$ (часто называемое условием регулярности ) тогда в сумме преобладает член расщепления $f(n)$ : $T\left(n\right)=\Theta \left(f(n)\right)$	Если $b=a^{2}$ и $f(n)=\Omega (n^{1/2+\epsilon })$ и условие регулярности выполнено, то $T(n)=\Theta (f(n))$ .

Полезное расширение варианта 2 обрабатывает все значения $k$ : ^[3]

Случай	Состояние включено $f(n)$ в связи с $c_{\operatorname {crit} }$ , то есть $\log _{b}a$	Основная теорема связана	Примеры обозначений
2а	Когда $f(n)=\Theta (n^{c_{\operatorname {crit} }}\log ^{k}n)$ для любого $k>-1$	... затем $T(n)=\Theta \left(n^{c_{\operatorname {crit} }}\log ^{k+1}n\right)$ (Граница — это член разделения, при котором журнал увеличивается на одну степень.)	Если $b=a^{2}$ и $f(n)=\Theta (n^{1/2}/\log ^{1/2}n)$ , затем $T(n)=\Theta (n^{1/2}\log ^{1/2}n)$ .
2б	Когда $f(n)=\Theta (n^{c_{\operatorname {crit} }}\log ^{k}n)$ для $k=-1$	... затем $T(n)=\Theta \left(n^{c_{\operatorname {crit} }}\log \log n\right)$ (Граница — это член разделения, где обратный логарифм заменяется итерированным логарифмом.)	Если $b=a^{2}$ и $f(n)=\Theta (n^{1/2}/\log n)$ , затем $T(n)=\Theta (n^{1/2}\log \log n)$ .
2с	Когда $f(n)=\Theta (n^{c_{\operatorname {crit} }}\log ^{k}n)$ для любого $k<-1$	... затем $T(n)=\Theta \left(n^{c_{\operatorname {crit} }}\right)$ (Граница — это член разделения, при котором журнал исчезает.)	Если $b=a^{2}$ и $f(n)=\Theta (n^{1/2}/\log ^{2}n)$ , затем $T(n)=\Theta (n^{1/2})$ .

Примеры [ править ]

Пример случая 1 [ править ]

T(n)=8T\left({\frac {n}{2}}\right)+1000n^{2}

Как видно из формулы выше:

a=8,\,b=2,\,f(n)=1000n^{2}

, так

f(n)=O\left(n^{c}\right)

, где

c=2

Далее мы проверим, удовлетворяем ли мы условию случая 1:

\log _{b}a=\log _{2}8=3>c

.

Из первого случая основной теоремы следует, что

T(n)=\Theta \left(n^{\log _{b}a}\right)=\Theta \left(n^{3}\right)

(Этот результат подтверждается точным решением рекуррентного соотношения, которое имеет вид $T(n)=1001n^{3}-1000n^{2}$ , предполагая $T(1)=1$ ).

Пример случая 2 [ править ]

$T(n)=2T\left({\frac {n}{2}}\right)+10n$

Как мы видим в формуле выше, переменные принимают следующие значения:

a=2,\,b=2,\,c=1,\,f(n)=10n

f(n)=\Theta \left(n^{c}\log ^{k}n\right)

где

c=1,k=0

Далее мы проверим, удовлетворяем ли мы условию случая 2:

\log _{b}a=\log _{2}2=1

, и, следовательно, c и

\log _{b}a

равны

Итак, из второго случая основной теоремы следует:

T(n)=\Theta \left(n^{\log _{b}a}\log ^{k+1}n\right)=\Theta \left(n^{1}\log ^{1}n\right)=\Theta \left(n\log n\right)

Таким образом, данное рекуррентное соотношение $T(n)$ был в $\Theta (n\log n)$ .

(Этот результат подтверждается точным решением рекуррентного соотношения, которое имеет вид $T(n)=n+10n\log _{2}n$ , предполагая $T(1)=1$ ).

Пример случая 3 [ править ]

T(n)=2T\left({\frac {n}{2}}\right)+n^{2}

Как мы видим в формуле выше, переменные принимают следующие значения:

a=2,\,b=2,\,f(n)=n^{2}

f(n)=\Omega \left(n^{c}\right)

, где

c=2

Далее мы проверим, удовлетворяем ли мы условию случая 3:

\log _{b}a=\log _{2}2=1

, и, следовательно, да,

c>\log _{b}a

Также выполнено условие регулярности:

2\left({\frac {n^{2}}{4}}\right)\leq kn^{2}

, выбирая

k=1/2

Так следует из третьего случая основной теоремы:

T\left(n\right)=\Theta \left(f(n)\right)=\Theta \left(n^{2}\right).

Таким образом, данное рекуррентное соотношение $T(n)$ был в $\Theta (n^{2})$ , что соответствует $f(n)$ исходной формулы.

(Этот результат подтверждается точным решением рекуррентного соотношения, которое имеет вид $T(n)=2n^{2}-n$ , предполагая $T(1)=1$ .)

Недопустимые уравнения [ править ]

Следующие уравнения не могут быть решены с помощью основной теоремы: ^[4]

$T(n)=2^{n}T\left({\frac {n}{2}}\right)+n^{n}$
а не является константой; количество подзадач должно быть исправлено
$T(n)=2T\left({\frac {n}{2}}\right)+{\frac {n}{\log n}}$
неполиномиальная разница между $f(n)$ и $n^{\log _{b}a}$ (см. ниже; применяется расширенная версия)
$T(n)=0.5T\left({\frac {n}{2}}\right)+n$
$a<1$ не может быть менее одной подпроблемы
$T(n)=64T\left({\frac {n}{8}}\right)-n^{2}\log n$
$f(n)$ , которое является временем комбинации, не является положительным
$T(n)=T\left({\frac {n}{2}}\right)+n(2-\cos n)$
случай 3, но нарушение регулярности.

Во втором недопустимом примере выше разница между $f(n)$ и $n^{\log _{b}a}$ можно выразить соотношением ${\frac {f(n)}{n^{\log _{b}a}}}={\frac {n/\log n}{n^{\log _{2}2}}}={\frac {n}{n\log n}}={\frac {1}{\log n}}$ . Ясно, что ${\frac {1}{\log n}}<n^{\epsilon }$ для любой константы $\epsilon >0$ . Следовательно, разница не является полиномиальной, и основная форма Главной теоремы не применима. Расширенная форма (случай 2b) применима и дает решение $T(n)=\Theta (n\log \log n)$ .

Приложение к общим алгоритмам [ править ]

Алгоритм	Рекуррентные отношения	Время выполнения	Комментарий
Бинарный поиск	$T(n)=T\left({\frac {n}{2}}\right)+O(1)$	$O(\log n)$	Применить случай основной теоремы $c=\log _{b}a$ , где $a=1,b=2,c=0,k=0$ ^[5]
Обход двоичного дерева	$T(n)=2T\left({\frac {n}{2}}\right)+O(1)$	$O(n)$	Применить случай основной теоремы $c<\log _{b}a$ где $a=2,b=2,c=0$ ^[5]
Поиск оптимальной сортированной матрицы	$T(n)=2T\left({\frac {n}{2}}\right)+O(\log n)$	$O(n)$	Примените теорему Акры–Бацци для $p=1$ и $g(u)=\log(u)$ получить $\Theta (2n-\log n)$
Сортировка слиянием	$T(n)=2T\left({\frac {n}{2}}\right)+O(n)$	$O(n\log n)$	Применить случай основной теоремы $c=\log _{b}a$ , где $a=2,b=2,c=1,k=0$

См. также [ править ]

Примечания [ править ]

^ Бентли, Джон Луис ; Хакен, Доротея ; Сакс, Джеймс Б. (сентябрь 1980 г.), «Общий метод решения повторяющихся задач по принципу «разделяй и властвуй»» , ACM SIGACT News , 12 (3): 36–44, doi : 10.1145/1008861.1008865 , S2CID 40642274 , заархивировано из оригинала 22 сентября 2017 г.
^ Университет Дьюка, «Большое спасибо за рекурсивные функции: рекуррентные отношения», http://www.cs.duke.edu/~ola/ap/recurrence.html
^ Чи Яп, Настоящий элементарный подход к основной повторяемости и обобщениям, Труды 8-й ежегодной конференции по теории и приложениям моделей вычислений (TAMC'11), страницы 14–26, 2011. Копия в Интернете.
^ Массачусетский технологический институт (MIT), «Главная теорема: практические проблемы и решения», https://people.csail.mit.edu/thies/6.046-web/master.pdf
^ Перейти обратно: ^а ^б Дартмутский колледж, http://www.math.dartmouth.edu/archive/m19w03/public_html/Section5-2.pdf

Ссылки [ править ]

Томас Х. Кормен , Чарльз Э. Лейзерсон , Рональд Л. Ривест и Клиффорд Стейн . Введение в алгоритмы , второе издание. MIT Press и МакГроу-Хилл, 2001. ISBN 0-262-03293-7 . Разделы 4.3 (Основной метод) и 4.4 (Доказательство основной теоремы), стр. 73–90.
Майкл Т. Гудрич и Роберто Тамассиа . Разработка алгоритмов: основы, анализ и примеры из Интернета . Уайли, 2002. ISBN 0-471-38365-1 . Основная теорема (включая включенную сюда версию случая 2, которая более сильная, чем версия из CLRS) находится на стр. 268–270.

[1] Бентли, Джон Луис ; Хакен, Доротея ; Сакс, Джеймс Б. (сентябрь 1980 г.), «Общий метод решения повторяющихся задач по принципу «разделяй и властвуй»» , ACM SIGACT News , 12 (3): 36–44, doi : 10.1145/1008861.1008865 , S2CID 40642274 , заархивировано из оригинала 22 сентября 2017 г.

[2] Университет Дьюка, «Большое спасибо за рекурсивные функции: рекуррентные отношения», http://www.cs.duke.edu/~ola/ap/recurrence.html

[Yap-3] Чи Яп, Настоящий элементарный подход к основной повторяемости и обобщениям, Труды 8-й ежегодной конференции по теории и приложениям моделей вычислений (TAMC'11), страницы 14–26, 2011. Копия в Интернете.

[4] Массачусетский технологический институт (MIT), «Главная теорема: практические проблемы и решения», https://people.csail.mit.edu/thies/6.046-web/master.pdf

[dartmouth-5] Перейти обратно: ^а ^б Дартмутский колледж, http://www.math.dartmouth.edu/archive/m19w03/public_html/Section5-2.pdf

[1]

[2]

[3]

[4]

[5]