Интеграл Пирси

График абсолютного значения интеграла Пирси как функции двух его параметров.

Фотография каустики выступа, полученная путем освещения плоской поверхности лазерным лучом через каплю воды.

В математике интеграл Пирси определяется как

$\operatorname {Pe} (x,y)=\int _{-\infty }^{\infty }\exp(i(t^{4}+xt^{2}+yt))\,dt.$

Интеграл Пирси — это класс канонических интегралов дифракции , часто используемых в распространения волн и оптической дифракции . задачах Первую численную оценку этого интеграла выполнил Тревор Пирси с использованием квадратурной формулы.

Светоотражающая каустика, созданная из круга и параллельных лучей. С одной стороны каждая точка содержится в трех световых лучах; с другой стороны, каждая точка содержится в одном световом луче.

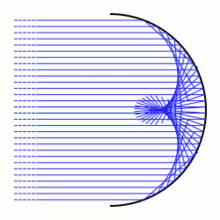
В оптике интеграл Пирси можно использовать для моделирования эффектов дифракции на каустике возврата , который соответствует границе между двумя областями геометрической оптики: с одной стороны каждая точка содержится в трех световых лучах; с другой стороны, каждая точка содержится в одном световом луче.