Теорема о максимальном потоке и минимальном сокращении

В информатике и теории оптимизации теорема о максимальном потоке и минимальном разрезе утверждает, что в проточной сети максимальный объем потока, проходящего от источника к стоку, равен общему весу ребер в минимальном разрезе , т. е. наименьший общий вес ребер, удаление которых приведет к отключению источника от стока.

Это частный случай теоремы двойственности для линейных программ , который можно использовать для вывода теоремы Менгера и теоремы Кенига-Эгервари . ^[1]

Определения и утверждения [ править ]

Теорема приравнивает две величины: максимальный поток через сеть и минимальную пропускную способность сечения сети. Чтобы сформулировать теорему, каждое из этих понятий необходимо сначала определить.

Сеть [ править ]

Сеть из состоит

конечный ориентированный граф $N = (V, E)$ , где V обозначает конечное множество вершин, а $E \subseteq V \times V$ — множество ориентированных ребер;
источник $s \in V$ и сток $t \in V$ ;
функция емкости , которая представляет собой отображение $c:E\to \mathbb {R} ^{+}$ обозначается $c uv$ или $c (u, v)$ для $(u, v) \in E$ . Он представляет собой максимальный объем потока, который может пройти через ребро.

Потоки [ править ]

Поток отображение через сеть представляет собой $f:E\to \mathbb {R} ^{+}$ обозначается $f_{uv}$ или $f(u,v)$ , при условии соблюдения следующих двух ограничений:

Ограничение емкости : для каждого края $(u,v)\in E$ , $f_{uv}\leq c_{uv}.$
Сохранение потоков : для каждой вершины $v$ Кроме $s$ и $t$ (т.е. источник и сток соответственно), имеет место следующее равенство:
$\sum \nolimits _{\{u:(u,v)\in E\}}f_{uv}=\sum \nolimits _{\{w:(v,w)\in E\}}f_{vw}.$

Поток можно представить как физический поток жидкости через сеть, следуя направлению каждого края. Тогда ограничение пропускной способности гласит, что объем, проходящий через каждое ребро в единицу времени, меньше или равен максимальной пропускной способности ребра, а ограничение сохранения гласит, что объем, поступающий в каждую вершину, равен объему, вытекающему из каждой вершины. кроме исходных и стоковых вершин.

Величина формулой потока определяется

|f|=\sum \nolimits _{\{v:(s,v)\in E\}}f_{sv}=\sum \nolimits _{\{v:(v,t)\in E\}}f_{vt},

где как указано выше $s$ является источником и $t$ является приемником сети. В аналогии с жидкостью он представляет собой количество жидкости, поступающей в сеть у источника. Из-за аксиомы сохранения потоков это то же самое, что и количество потока, покидающего сеть в стоке.

Задача о максимальном потоке требует максимального потока в данной сети.

Проблема максимального потока. Максимизировать $|f|$ , то есть направить как можно больший поток от $s$ к $t$ .

Сокращения [ править ]

Другая половина теоремы о максимальном потоке и минимальном разрезе относится к другому аспекту сети: набору разрезов. St разрез $C = (S, T)$ — это разбиение $V$ такое, $s \in S$ и $t \in T.$ что То есть разрез s — t — это разделение вершин сети на две части, с источником в одной части и стоком в другой. Набор вырезок $X_{C}$ разреза $C$ — множество ребер, соединяющих источную часть разреза со стоковой частью:

X_{C}:=\{(u,v)\in E\ :\ u\in S,v\in T\}=(S\times T)\cap E.

Таким образом, если все ребра в разрезе $C$ удалены, положительный поток невозможен, поскольку в результирующем графе нет пути от источника к стоку.

поперечного Пропускная способность разреза равна сумме пропускных способностей ребер в его наборе разрезов.

c(S,T)=\sum \nolimits _{(u,v)\in X_{C}}c_{uv}=\sum \nolimits _{(i,j)\in E}c_{ij}d_{ij},

где $d_{ij}=1$ если $i\in S$ и $j\in T$ , $0$ в противном случае.

Обычно в графе много разрезов, но найти разрезы с меньшими весами зачастую труднее.

Проблема с минимальным вырезом. Минимизируйте

c (S, T)

, то есть определите

S

и

T

так, чтобы пропускная способность st разреза была минимальной.

Основная теорема [ править ]

В приведенной выше ситуации можно доказать, что значение любого потока через сеть меньше или равно пропускной способности любого st разреза и что, кроме того, существуют поток с максимальным значением и разрез с минимальной пропускной способностью. Основная теорема связывает максимальное значение потока с минимальной пропускной способностью сети.

Теорема о максимальном потоке и минимальном сокращении. Максимальное значение расхода st равно минимальной производительности по всем разрезам st.

Пример [ править ]

На рисунке справа показан поток в сети. Числовая аннотация на каждой стрелке в форме f / c указывает расход ( f ) и пропускную способность ( c ) стрелки. Всего потоков, исходящих из источника, пять (2+3=5), как и потоков в сток (2+3=5), что означает, что значение потока равно 5.

Один разрез s - t со значением 5 задается S = { s , p } и T = { o , q , r , t }. Пропускные способности ребер, пересекающих этот разрез, равны 3 и 2, что дает пропускную способность разреза 3+2=5. (Стрелка от o до p не рассматривается, так как она указывает от T обратно к S. )

Величина потока равна пропускной способности разреза, что указывает на то, что поток является максимальным потоком, а разрез - минимальным.

Обратите внимание, что поток через каждую из двух стрелок, соединяющих S и T, работает на полную мощность; так всегда бывает: минимальное сокращение представляет собой «узкое место» системы.

линейной Формулировка программы

Задачу максимального потока и задачу минимального сокращения можно сформулировать как две первично-двойственные линейные программы . ^[2]

	Максимальный поток (Первоначальный)	Минимальный вырез (двойной)
переменные	$f_{uv}$ $\forall (u,v)\in E$ [две переменные на каждое ребро, по одной в каждом направлении]	$d_{uv}$ $\forall (u,v)\in E$ [переменная на ребро] $z_{v}$ $\forall v\in V\setminus \{s,t\}$ [переменная для каждого нетерминального узла]
цель	максимизировать $\sum \nolimits _{v:(s,v)\in E}f_{sv}$ [максимальный общий поток из источника]	минимизировать $\sum \nolimits _{(u,v)\in E}c_{uv}d_{uv}$ [минимальная общая мощность кромок в разрезе]
ограничения	при условии ${\begin{aligned}f_{uv}&\leq c_{uv}&&\forall (u,v)\in E\\\sum _{u}f_{uv}-\sum _{w}f_{vw}&=0&&v\in V\setminus \{s,t\}\end{aligned}}$ [ограничение на ребро и ограничение на нетерминальный узел]	при условии ${\begin{aligned}d_{uv}-z_{u}+z_{v}&\geq 0&&\forall (u,v)\in E,u\neq s,v\neq t\\d_{sv}+z_{v}&\geq 1&&\forall (s,v)\in E,v\neq t\\d_{ut}-z_{u}&\geq 0&&\forall (u,t)\in E,u\neq s\\d_{st}&\geq 1&&{\text{if }}(s,t)\in E\end{aligned}}$ [ограничение на ребро]
знак ограничения	${\begin{aligned}f_{uv}&\geq 0&&\forall (u,v)\in E\\\end{aligned}}$	${\begin{aligned}d_{uv}&\geq 0&&\forall (u,v)\in E\\z_{v}&\in \mathbb {R} &&\forall v\in V\setminus \{s,t\}\end{aligned}}$

Максимальный поток LP прост. Двойственный ЛП получается с использованием алгоритма, описанного в двойной линейной программе : переменные и знаковые ограничения двойственного элемента соответствуют ограничениям основного элемента, а ограничения двойственного элемента соответствуют переменным и знаковым ограничениям основного элемента. Полученный ЛП требует некоторых пояснений. Интерпретация переменных в минимальном сокращении LP:

d_{uv}={\begin{cases}1,&{\text{if }}u\in S{\text{ and }}v\in T{\text{ (the edge }}uv{\text{ is in the cut) }}\\0,&{\text{otherwise}}\end{cases}}

z_{v}={\begin{cases}1,&{\text{if }}v\in S\\0,&{\text{otherwise}}\end{cases}}

Цель минимизации суммирует пропускную способность по всем ребрам, содержащимся в разрезе.

Ограничения гарантируют, что переменные действительно представляют собой допустимый разрез: ^[3]

Ограничения $d_{uv}-z_{u}+z_{v}\geq 0$ (эквивалентно $d_{uv}\geq z_{u}-z_{v}$ ) гарантируют, что для нетерминальных узлов u,v , если u находится в S , а v находится в T , то ребро ( u , v ) учитывается в разрезе ( $d_{uv}\geq 1$ ).
Ограничения $d_{sv}+z_{v}\geq 1$ (эквивалентно $d_{sv}\geq 1-z_{v}$ ) гарантируют, что если v находится в T , то ребро (s,v) учитывается в разрезе (поскольку s по определению находится в S ).
Ограничения $d_{ut}-z_{u}\geq 0$ (эквивалентно $d_{ut}\geq z_{u}$ ) гарантируют, что если u находится в S , то ребро (u,t) учитывается в разрезе (поскольку t по определению находится в T ).

Обратите внимание: поскольку это задача минимизации, нам не нужно гарантировать, что ребро не находится в разрезе — нам нужно только гарантировать, что каждое ребро, которое должно быть в разрезе, суммируется в целевой функции.

Равенство в теореме о максимальном потоке и минимальном сокращении следует из сильной теоремы двойственности в линейном программировании , которая утверждает, что если основная программа имеет оптимальное решение x *, то двойственная программа также имеет оптимальное решение y *, такое что оптимальные значения, образованные двумя решениями, равны.

Приложение [ править ]

Седербаума о потоке максимальном Теорема

Задачу максимального потока можно сформулировать как максимизацию электрического тока через сеть, состоящую из нелинейных резистивных элементов. ^[4] В этой формулировке предел тока $I между$ входными клеммами электрической сети при входном напряжении $V приближается$ к $\infty$ , равен весу набора отсечений минимального веса.

\lim _{V_{\text{in}}\to \infty }(I_{in})=\min _{X_{C}}\sum _{(u,v)\in X_{C}}c_{uv}

о максимальном потоке и минимальном сокращении Обобщенная теорема

Помимо пропускной способности ребра, учтите, что в каждой вершине имеется пропускная способность, то есть отображение $c:V\to \mathbb {R} ^{+}$ обозначается $c (v)$ , так что поток $f$ должен удовлетворять не только ограничению пропускной способности и сохранению потоков, но также ограничению пропускной способности вершин

\forall v\in V\setminus \{s,t\}:\qquad \sum \nolimits _{\{u\in V\mid (u,v)\in E\}}f_{uv}\leq c(v).

Другими словами, количество потока , проходящего через вершину, не может превышать ее пропускную способность. Определите разрез st как набор вершин и ребер, такой, что для любого пути от s до t путь содержит член разреза. В этом случае емкость разреза равна сумме емкостей каждого ребра и вершины в нем.

В этом новом определении обобщенная теорема о максимальном потоке и минимальном разрезе утверждает, что максимальное значение st-потока равно минимальной пропускной способности st-разреза в новом смысле.

Теорема Менгера [ править ]

В задаче о ненаправленных путях, не пересекающихся по ребрам, нам дан неориентированный граф $G = (V, E)$ и две вершины $s$ и $t$ , и нам нужно найти максимальное количество путей st, не пересекающихся по ребрам, в $G$ .

Теорема Менгера утверждает, что максимальное количество непересекающихся по ребрам st путей в неориентированном графе равно минимальному количеству ребер в st разрезном множестве.

Проблема выбора проекта [ править ]

В задаче выбора проекта имеется $n$ проектов и $m$ машин. Каждый проект $p i$ приносит доход $r (p i)$ каждой машины $q j$ обходится в $c (q j)$ , а покупка . Для каждого проекта требуется несколько машин, и каждая машина может использоваться несколькими проектами. Проблема состоит в том, чтобы определить, какие проекты и машины следует выбрать и закупить соответственно, чтобы прибыль была максимальной.

Пусть $P$ — набор не выбранных проектов, а $Q$ — набор закупленных машин, тогда проблему можно сформулировать следующим образом:

\max\{g\}=\sum _{i}r(p_{i})-\sum _{p_{i}\in P}r(p_{i})-\sum _{q_{j}\in Q}c(q_{j}).

Поскольку первое слагаемое не зависит от выбора $P$ и $Q$ , эту задачу максимизации можно вместо этого сформулировать как задачу минимизации, т. е.

\min\{g'\}=\sum _{p_{i}\in P}r(p_{i})+\sum _{q_{j}\in Q}c(q_{j}).

Вышеупомянутую задачу минимизации затем можно сформулировать как задачу минимального сечения путем построения сети, в которой источник подключен к проектам с мощностью $r (pi c)$ , а приемник подключен к машинам с мощностью $(q j) .$ . Ребро $(pi проекта, qj производительностью)$ с бесконечной добавляется, если $требуется pi$ машина $qj .$ для Первый набор разрезов представляет проекты и машины в $P$ и $Q$ соответственно. По теореме о максимальном потоке и минимальном сокращении эту проблему можно решить как задачу о максимальном потоке .

На рисунке справа представлена сетевая формулировка следующей задачи выбора проекта:

	Проект $р (п я)$	Машина $c (q j)$
1	100	200	Для проекта 1 требуются машины 1 и 2.
2	200	100	Для проекта 2 требуется машина 2.
3	150	50	Для проекта 3 требуется машина 3.

Минимальная мощность одного разреза — 250, а сумма доходов каждого проекта — 450; следовательно, максимальная прибыль g равна 450 - 250 = 200 при выборе проектов $p 2$ и $p 3$ .

Идея здесь состоит в том, чтобы «пропустить» прибыль каждого проекта через «трубы» его машин. Если мы не можем заполнить трубу с помощью машины, прибыль машины будет меньше, чем ее стоимость, и алгоритм минимального сокращения сочтет, что дешевле сократить прибыль проекта, а не стоимость машины.

Проблема с сегментацией изображения [ править ]

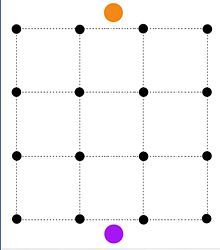
В задаче сегментации изображения имеется $n$ пикселей. Каждому пикселю $i$ может быть присвоено значение переднего плана $f i$ или значение фона $b i$ . Существует штраф $pij,$ если пиксели $i, j$ соседние и имеют разные назначения. Проблема состоит в том, чтобы назначить пиксели переднему или заднему плану так, чтобы сумма их значений за вычетом штрафов была максимальной.

Пусть $P$ — набор пикселей, назначенных переднему плану, а $Q$ — набор точек, назначенных фону, тогда проблему можно сформулировать следующим образом:

\max\{g\}=\sum _{i\in P}f_{i}+\sum _{i\in Q}b_{i}-\sum _{i\in P,j\in Q\lor j\in P,i\in Q}p_{ij}.

Вместо этого эту задачу максимизации можно сформулировать как задачу минимизации, т. е.

\min\{g'\}=\sum _{i\in P,j\in Q\lor j\in P,i\in Q}p_{ij}.

Вышеупомянутую задачу минимизации можно сформулировать как задачу минимального сечения путем построения сети, в которой источник (оранжевый узел) соединен со всеми пикселями с емкостью $f i$ , а сток (фиолетовый узел) соединен со всеми пикселями с емкостью $б я$ . Два ребра ( $i, j$ ) и ( $j, i$ ) с $пропускной способностью p ij$ добавляются между двумя соседними пикселями. Затем первый набор вырезов представляет пиксели, назначенные переднему плану в $P,$ пиксели, назначенные фону в $Q.$ и

История [ править ]

Отчет об открытии теоремы был сделан Фордом и Фулкерсоном в 1962 году: ^[5]

«Определение максимального установившегося потока из одной точки в другую в сети с учетом ограничений пропускной способности дуг... было поставлено перед авторами весной 1955 года Т.Э. Харрисом, который совместно с генералом Ф.С. Россом (в отставке) сформулировал упрощенную модель железнодорожных транспортных потоков и определил эту конкретную проблему как центральную, предложенную моделью. Вскоре после этого был получен основной результат, теорема 5.1, которую мы называем теоремой о максимальном потоке и минимальном сокращении. было предположено и установлено. ^[6] С тех пор появился ряд доказательств». ^[7]^[8]^[9]

Доказательство [ править ]

Пусть $G = (V, E)$ — сеть (ориентированный граф), где $s$ и $t$ являются источником и стоком $G$ соответственно.

Рассмотрим поток $f,$ вычисленный для $G$ по алгоритму Форда–Фалкерсона . остаточном графе $(Gf В),$ полученном для $G$ (после окончательного назначения потока алгоритмом Форда–Фалкерсона ), определите два подмножества вершин следующим образом:

$A$ : набор вершин, достижимых из $s$ в $G f$
$А с$ : набор оставшихся вершин, т.е. $V - A$

Требовать. $значение(f) = c (A, A с)$ , где пропускная способность первого разреза определяется выражением

c(S,T)=\sum \nolimits _{(u,v)\in S\times T}c_{uv}

.

Теперь мы знаем, $value(f)=f_{out}(A)-f_{in}(A)$ для любого подмножества вершин $A$ . Следовательно, для $value(f) = c (A, A с)$ нам нужно:

Все края, выходящие из разреза, должны быть полностью пропитаны .
Все входящие в разрез кромки должны иметь нулевой поток .

Для доказательства вышеизложенного утверждения рассмотрим два случая:

В $G$ существует выходящее ребро $(x,y),x\in A,y\in A^{c}$ такой, что он не насыщен, т. е. $f (x, y) < c xy$ . означает, что существует прямое ребро от $x$ до $y$ в $Gf Это$ существует путь от $s$ до $y$ в $Gf, следовательно ,$ , что является противоречием. Следовательно, любое исходящее ребро $(x, y)$ полностью насыщено.

В $G$ существует входящее ребро $(y,x),x\in A,y\in A^{c}$ такой, что он несет некоторый ненулевой поток, т. е. $f (y, x) > 0$ . Это означает, что существует обратное ребро от $x$ до $y$ в $G f$ , следовательно, существует путь от $s$ до $y$ в $G f$ , что снова является противоречием. Следовательно, любое входящее ребро $(y, x)$ должно иметь нулевой поток.

Оба приведенных утверждения доказывают, что пропускная способность полученного вышеописанным способом разреза равна потоку, полученному в сети. Кроме того, поток был получен с помощью алгоритма Форда-Фалкерсона , поэтому он также является максимальным потоком сети.

Кроме того, поскольку любой поток в сети всегда меньше или равен пропускной способности каждого возможного разреза в сети, описанный выше разрез также является минимальным разрезом , который обеспечивает максимальный поток .

Следствием этого доказательства является то, что максимальный поток через любой набор ребер разреза графа равен минимальной пропускной способности всех предыдущих разрезов.

См. также [ править ]

Ссылки [ править ]

^ Данциг, Великобритания; Фулкерсон, Д.Р. (9 сентября 1964 г.). «О теореме сетей о максимальном потоке и минимальном разрезе» (PDF) . RAND Corporation : 13. Архивировано из оригинала (PDF) 5 мая 2018 года.
^ Тревизан, Лука. «Лекция 15 из CS261: Оптимизация» (PDF) .
^ Келлер, Оргад. «Презентация LP min-cut max-flow» .
^ Седербаум, И. (август 1962 г.). «Об оптимальной эксплуатации сетей связи». Журнал Института Франклина . 274 : 130–141.
^ Л.Р. Форд-младший и Д.Р. Фулкерсон (1962) Потоки в сетях , стр. 1, Princeton University Press, MR 0159700
^ Л.Р. Форд-младший и Д.Р. Фулкерсон (1956) «Максимальный поток через сеть», Canadian Journal of Mathematics 8: 399-404
^ П. Элиас, А. Файнштейн и К. Э. Шеннон (1956) «Заметка о максимальном потоке через сеть», IRE. Труды по теории информации, 2 (4): 117–119.
^ Джордж Данциг и Д. Р. Фулкерсон (1956) «О теореме сетей о максимальном потоке и минимальном сокращении», в « Линейные неравенства» , Ann. Математика. Исследования, нет. 38, Принстон, Нью-Джерси
^ Л. Р. Форд и Д. Р. Фулкерсон (1957) «Простой алгоритм поиска максимальных сетевых потоков и приложение к проблеме Хичкока», Canadian Journal of Mathematics 9: 210–18.

Юджин Лоулер (2001). «4.5. Комбинаторные следствия теоремы о минимальном разрезе о максимальном потоке, 4.6. Интерпретация линейного программирования теоремы о минимальном разрезе о максимальном потоке». Комбинаторная оптимизация: сети и матроиды . Дувр. стр. 117–120. ISBN 0-486-41453-1 .
Христос Х. Пападимитриу , Кеннет Стейглиц (1998). «6.1 Теорема о максимальном потоке и минимальном сокращении». Комбинаторная оптимизация: алгоритмы и сложность . Дувр. стр. 120–128. ISBN 0-486-40258-4 .
Виджай В. Вазирани (2004). «12. Введение в ЛП-Дуальность». Алгоритмы аппроксимации . Спрингер. стр. 93–100. ISBN 3-540-65367-8 .

[1] Данциг, Великобритания; Фулкерсон, Д.Р. (9 сентября 1964 г.). «О теореме сетей о максимальном потоке и минимальном разрезе» (PDF) . RAND Corporation : 13. Архивировано из оригинала (PDF) 5 мая 2018 года.

[2] Тревизан, Лука. «Лекция 15 из CS261: Оптимизация» (PDF) .

[3] Келлер, Оргад. «Презентация LP min-cut max-flow» .

[4] Седербаум, И. (август 1962 г.). «Об оптимальной эксплуатации сетей связи». Журнал Института Франклина . 274 : 130–141.

[5] Л.Р. Форд-младший и Д.Р. Фулкерсон (1962) Потоки в сетях , стр. 1, Princeton University Press, MR 0159700

[6] Л.Р. Форд-младший и Д.Р. Фулкерсон (1956) «Максимальный поток через сеть», Canadian Journal of Mathematics 8: 399-404

[7] П. Элиас, А. Файнштейн и К. Э. Шеннон (1956) «Заметка о максимальном потоке через сеть», IRE. Труды по теории информации, 2 (4): 117–119.

[8] Джордж Данциг и Д. Р. Фулкерсон (1956) «О теореме сетей о максимальном потоке и минимальном сокращении», в « Линейные неравенства» , Ann. Математика. Исследования, нет. 38, Принстон, Нью-Джерси

[9] Л. Р. Форд и Д. Р. Фулкерсон (1957) «Простой алгоритм поиска максимальных сетевых потоков и приложение к проблеме Хичкока», Canadian Journal of Mathematics 9: 210–18.

[1]

[2]

[3]

[4]

[5]

[6]

[7]

[8]

[9]