Коэффициент получения информации

В обучении дерева решений коэффициент прироста информации — это отношение прироста информации к внутренней информации. Его предложил Росс Куинлан . ^[1] уменьшить перекос в сторону многозначных атрибутов, принимая во внимание количество и размер ветвей при выбореатрибут. ^[2]

Получение информации также известно как взаимная информация . ^[3]

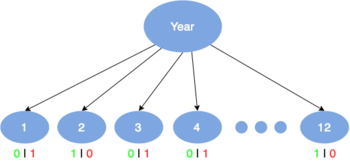
На изображении показан прирост информации от переменной под названием «год» и результат выбора года от 1 до 12. Прирост информации будет в пользу этой переменной, поскольку результаты будут либо определенно положительными, либо отрицательными, но при этом будут создаваться несколько конечных узлов. Проблема в том, что ни один из этих лет не повторится. Следующим вводом будет 13-й год, но перехода к 13-му году нет, и эту проблему можно решить с помощью коэффициента прироста информации. Коэффициент прироста информации нормализует данные, используя значение энтропии этой переменной, чтобы устранить смещение данных с несколькими переменными и переменных с несколькими узлами по сравнению с переменными с меньшим набором узлов. Это устранит вероятность создания дерева на изображении.

Расчет получения информации

Прирост информации — это уменьшение энтропии, возникающее в результате разделения набора по атрибутам. $a$ и находим оптимального кандидата, который дает наибольшее значение:

{\text{IG}}(T,a)=\mathrm {H} {(T)}-\mathrm {H} {(T|a)},

где $T$ является случайной величиной и $\mathrm {H} {(T|a)}$ это энтропия $T$ учитывая значение атрибута $a$ .

Прирост информации равен общей энтропии атрибута, если для каждого значения атрибута можно провести уникальную классификацию результирующего атрибута. В этом случае относительная энтропия, вычтенная из общей энтропии, равна 0.

Расчет разделенной информации

Значение разделенной информации для теста определяется следующим образом:

${\text{SplitInformation}}(X)=-\sum _{i=1}^{n}{{\frac {\mathrm {N} (x_{i})}{\mathrm {N} (x)}}*\log {_{2}}{\frac {\mathrm {N} (x_{i})}{\mathrm {N} (x)}}}$

где $X$ — дискретная случайная величина с возможными значениями ${x_{1},x_{2},...,x_{i}}$ и $N(x_{i})$ количество раз, которое $x_{i}$ происходит, разделенное на общее количество событий $N(x)$ где $x$ это совокупность событий.

Значение информации о разделении — это положительное число, которое описывает потенциальную ценность отделения ветви от узла. Это, в свою очередь, является внутренней ценностью, которой обладает случайная величина и которая будет использоваться для устранения систематической ошибки при расчете коэффициента прироста информации.

Расчет коэффициента прироста информации

Коэффициент прироста информации — это соотношение между приростом информации и значением разделенной информации: ${\text{IGR}}(T,a)={\text{IG}}(T,a)/{\text{SplitInformation}}(T)$

${\text{IGR}}(T,a)={\frac {-\sum _{i=1}^{n}{\mathrm {P} (T)\log \mathrm {P} (T)}-(-\sum _{i=1}^{n}{\mathrm {P} (T|a)\log \mathrm {P} (T|a)})}{-\sum _{i=1}^{n}{{\frac {\mathrm {N} (t_{i})}{\mathrm {N} (t)}}*\log {_{2}}{\frac {\mathrm {N} (t_{i})}{\mathrm {N} (t)}}}}}$

Пример

Используя данные о погоде, опубликованные Университетом Фордхэма, ^[4] таблица была создана ниже:

Данные о погоде WEKA
Перспективы	Температура	Влажность	Ветер	Играть
Солнечно	Горячий	Высокий	ЛОЖЬ	Нет
Солнечно	Горячий	Высокий	Истинный	Нет
Пасмурно	Горячий	Высокий	ЛОЖЬ	Да
Дождливый	Мягкий	Высокий	ЛОЖЬ	Да
Дождливый	Прохладный	Нормальный	ЛОЖЬ	Да
Дождливый	Прохладный	Нормальный	Истинный	Нет
Пасмурно	Прохладный	Нормальный	Истинный	Да
Солнечно	Мягкий	Высокий	ЛОЖЬ	Нет
Солнечно	Прохладный	Нормальный	ЛОЖЬ	Да
Дождливый	Мягкий	Нормальный	ЛОЖЬ	Да
Солнечно	Мягкий	Нормальный	ЛОЖЬ	Да
Пасмурно	Мягкий	Высокий	Истинный	Да
Пасмурно	Горячий	Нормальный	ЛОЖЬ	Да
Дождливый	Мягкий	Высокий	Истинный	Нет

Используя приведенную выше таблицу, можно найти энтропию, прирост информации, разделение информации и коэффициент прироста информации для каждой переменной (прогноз, температура, влажность и ветер). Эти расчеты показаны в таблицах ниже:

Таблица Outlook
Перспективы	Да	Нет	Количество каждой группы	Энтропия
солнечный	2	3	5	0.971
пасмурно	4	0	4	0.000
дождливый	3	2	5	0.971
Результаты	Ценности
Информация	0.694
Общая энтропия	0.940
Получение информации	0.247
Разделить информацию	1.577
Коэффициент усиления	0.156

Таблица температур
Температура	Да	Нет	Количество каждой группы	Энтропия
горячий	2	2	4	1.000
мягкий	4	2	6	0.918
прохладный	3	1	4	0.811
Результаты	Ценности
Информация	0.911
Общая энтропия	0.940
Получение информации	0.029
Разделить информацию	1.557
Коэффициент усиления	0.019

Ветровой стол
Ветер	Да	Нет	Количество каждой группы	Энтропия
ЛОЖЬ	6	2	8	0.811
Истинный	3	3	6	1.000
Результаты	Ценности
Информация	0.892
Общая энтропия	0.940
Получение информации	0.048
Разделить информацию	0.985
Коэффициент усиления	0.049

Таблица влажности
Влажность	Да	Нет	Количество каждой группы	Энтропия
Высокий	3	4	7	0.985
Нормальный	6	1	7	0.592
Результаты	Ценности
Информация	0.788
Общая энтропия	0.940
Получение информации	0.152
Разделить информацию	1.000
Коэффициент усиления	0.152

Используя приведенные выше таблицы, можно сделать вывод, что Outlook имеет самый высокий коэффициент получения информации. Далее необходимо найти статистику для подгрупп переменной Outlook (солнечно, пасмурно и дождливо), для этого примера будет построена только солнечная ветка (как показано в таблице ниже):

Таблица Outlook
Перспективы	Температура	Влажность	Ветер	Играть
Солнечно	Горячий	Высокий	ЛОЖЬ	Нет
Солнечно	Горячий	Высокий	Истинный	Нет
Солнечно	Мягкий	Высокий	ЛОЖЬ	Нет
Солнечно	Прохладный	Нормальный	ЛОЖЬ	Да
Солнечно	Мягкий	Нормальный	Истинный	Да

Можно найти следующую статистику для других переменных (температура, влажность и ветер), чтобы увидеть, какие из них оказывают наибольшее влияние на солнечный элемент переменной прогноза:

Таблица температур
Температура	Да	Нет	Количество каждой группы	Энтропия
Горячий	0	2	2	0.000
Мягкий	1	1	2	1.000
Прохладный	1	0	1	0.000
Результаты	Ценности
Информация	0.400
Общая энтропия	0.971
Прирост	0.571
Разделить информацию	1.522
Коэффициент усиления	0.375

Ветровой стол
Ветер	Да	Нет	Количество каждой группы	Энтропия
ЛОЖЬ	1	2	3	0.918
Истинный	1	1	2	1.000
Результаты	Ценности
Информация	0.951
Общая энтропия	0.971
Прирост	0.020
Разделить информацию	0.971
Коэффициент усиления	0.021

Таблица влажности
Влажность	Да	Нет	Количество каждой группы	Энтропия
Высокий	0	3	3	0.000
Нормальный	2	0	2	0.000
Результаты	Ценности
Информация	0.000
Общая энтропия	0.971
Прирост	0.971
Разделить информацию	0.971
Коэффициент усиления	1.000

Было обнаружено, что влажность имеет самый высокий коэффициент получения информации. Повторим те же шаги, что и раньше, и найдем статистику событий переменной Влажность (высокая и нормальная):

Стол с высокой влажностью
Влажность	Ветер	Играть
Высокий	ЛОЖЬ	Нет
Высокий	Истинный	Нет
Высокий	ЛОЖЬ	Нет

Таблица влажности-норма
Влажность	Ветер	Играть
Нормальный	ЛОЖЬ	Да
Нормальный	Истинный	Да

Поскольку игровые значения либо «Нет», либо «Да», значение коэффициента прироста информации будет равно 1. Кроме того, теперь, когда мы достигли конца цепочки переменных, где Wind является последней оставшейся переменной, они могут построить вся ветвь от корня к конечному узлу дерева решений.

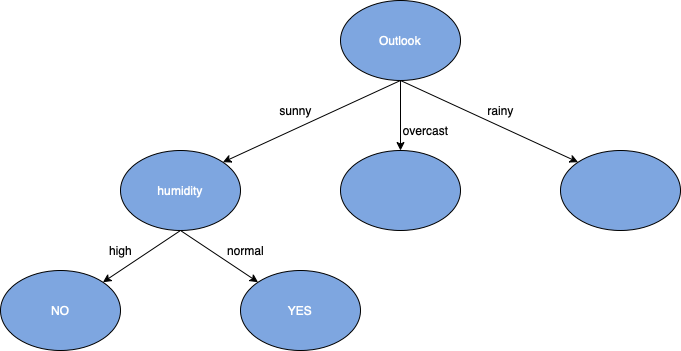
После достижения этого листового узла можно будет выполнить ту же процедуру для остальных элементов, которые еще не были разделены в дереве решений. Этот набор данных был относительно небольшим, однако, если использовался больший набор, преимущества использования коэффициента прироста информации в качестве коэффициента разделения дерева решений можно было увидеть больше.

Преимущества

Коэффициент прироста информации искажает дерево решений , не позволяя учитывать атрибуты с большим количеством различных значений.

Например, предположим, что мы строим дерево решений для некоторых данных, описывающих клиентов компании. Коэффициент прироста информации используется для принятия решения о том, какие из атрибутов являются наиболее релевантными. Они будут проверены возле корня дерева. клиента Одним из входных атрибутов может быть номер телефона . Этот атрибут имеет высокую информационную ценность, поскольку он однозначно идентифицирует каждого клиента. Из-за большого количества различных значений он не будет выбран для проверки вблизи корня.

Недостатки

Хотя коэффициент прироста информации решает ключевую проблему прироста информации, он создает еще одну проблему. Если рассматривать количество атрибутов, имеющих большое количество различных значений, оно никогда не будет больше атрибута с меньшим количеством различных значений.

Отличие от получения информации

Недостаток прироста информации возникает из-за отсутствия численной разницы между атрибутами с высокими отличными значениями и атрибутами с меньшими значениями.
- Пример: предположим, что мы строим дерево решений для некоторых данных, описывающих клиентов компании. Полученная информация часто используется для принятия решения о том, какие из атрибутов являются наиболее релевантными, поэтому их можно проверить вблизи корня дерева. клиента Одним из входных атрибутов может быть номер кредитной карты . Этот атрибут дает высокую информационную выгоду, поскольку он уникально идентифицирует каждого клиента, но мы не хотим включать его в дерево решений: решение о том, как обращаться с клиентом на основе номера его кредитной карты, вряд ли будет распространяться на клиентов, которых у нас нет. видел раньше.
Сильная сторона коэффициента прироста информации заключается в том, что он имеет уклон в сторону атрибутов с меньшим количеством различных значений.
Ниже приведена таблица, описывающая различия в приросте информации и коэффициенте прироста информации в определенных сценариях.

Ситуационные различия между приростом информации и коэффициентом прироста информации
Получение информации	Коэффициент получения информации
Не будет отдавать предпочтение каким-либо атрибутам по количеству различных значений.	Предпочитает атрибут с меньшим количеством различных значений.
При применении к атрибутам, которые могут принимать большое количество различных значений, этот метод может изучить обучающий набор. слишком хорошо	Пользователю будет сложно найти атрибуты, требующие большого количества различных значений.

См. также

Ссылки

^ Куинлан, младший (1986). «Индукция деревьев решений» . Машинное обучение . 1 : 81–106. дои : 10.1007/BF00116251 .
^ http://www.ke.tu-darmstadt.de/lehre/archiv/ws0809/mldm/dt.pdf . Архивировано 28 декабря 2014 г. в Wayback Machine. ^{[ пустой URL PDF ]}
^ «Получение информации, взаимное информирование и связанные с этим меры» .
^ https://storm.cis.fordham.edu/~gweiss/data-mining/weka-data/weather.nominal.arff

[1] Куинлан, младший (1986). «Индукция деревьев решений» . Машинное обучение . 1 : 81–106. дои : 10.1007/BF00116251 .

[2] ttp://www.ke.tu-darmstadt.de/lehre/archiv/ws0809/mldm/dt.pdf . Архивировано 28 декабря 2014 г. в Wayback Machine. ^{[ пустой URL PDF ]}

[3] «Получение информации, взаимное информирование и связанные с этим меры» .

[4] ttps://storm.cis.fordham.edu/~gweiss/data-mining/weka-data/weather.nominal.arff

[1]

[2]

[3]

[4]