Минимальное связующее дерево с узким местом

В математике минимальное связующее дерево с узким местом (MBST) в неориентированном графе — это связующее дерево , в котором самое дорогое ребро является максимально дешевым. Ребро узкого места — это ребро с наибольшим весом в связующем дереве. Охватывающее дерево является минимальным связующим деревом с узким местом, если граф не содержит остовное дерево с меньшим весом ребра узкого места. ^[1] Для ориентированного графа аналогичная проблема известна как «Минимальное узкое место, охватывающее древовидность» (MBSA) .

Определения

Неориентированные графы

Минимальное связующее дерево с узкими местами ⁠ $G(V,E)$ ⁠

В неориентированном графе $G (V, E)$ функции $w : E \to R$ пусть $S$ — множество всех остовных деревьев Ti _и . Пусть B ( Ti _{остовного} ) — ребро максимального веса для любого Ti _дерева . Мы определяем подмножество минимальных узких остовных деревьев S ′ такое, что для каждых $T j \in S'$ и $T k \in S$ мы имеем $B (T j) ⩽ B (T k)$ для всех i и k . ^[2]

Граф справа является примером MBST, красные ребра на графике образуют MBST $G (V, E)$ .

Ориентированные графы

Древовидность графа G — это направленное дерево графа G , содержащее направленный путь от заданного узла L до каждого узла подмножества V ′ из $V \{ L }$ . Узел L называется корнем древовидности. Древовидность является охватывающей древовидностью, если $V ′ = V \{ L }$ . MBST в данном случае представляет собой пролетное ветвление с минимальным краем узкого места. MBST в этом случае называется минимальным узким местом, охватывающим древовидность (MBSA).

Граф справа является примером MBSA, красные ребра на графике образуют MBSA $G (V, E)$ .

Характеристики

MST (или минимальное связующее дерево ) обязательно является MBST, но MBST не обязательно является MST. ^[3]

^[4]

Алгоритм Камерини для неориентированных графов

Предлагаются раздевалки ^[5] алгоритм , используемый для получения минимального связующего дерева с узкими местами (MBST) в заданном неориентированном связном графе с взвешиванием по ребрам в 1978 году. Он делит ребра наполовину на два набора. Веса ребер в одном наборе не больше, чем в другом. Если остовное дерево существует в подграфе, состоящем исключительно из ребер из набора меньших ребер, оно затем вычисляет MBST в подграфе, MBST подграфа в точности является MBST исходного графа. Если связующее дерево не существует, оно объединяет каждый несвязный компонент в новую супервершину, а затем вычисляет MBST в графе, образованном этими супервершинами и ребрами в большем наборе ребер. Лес в каждом несвязном компоненте является частью MBST в исходном графе. Повторяйте этот процесс до тех пор, пока в графе не останется две (супер) вершины и между ними не будет добавлено одно ребро с наименьшим весом. Находится MBST, состоящий из всех ребер, найденных на предыдущих шагах. ^[4]

Псевдокод

Процедура имеет два входных параметра. G — граф, w массив весов всех ребер в графе G. — ^[6]

function MBST(graph G, weights w)
    E ← the set of edges of G 
    if | E | = 1 then return E else
        A ← half edges in E whose weights are no less than the median weight
        B ← E - A
        F ← forest of G_B
        if F is a spanning tree then
            return MBST(G_B,w)
        else
            return MBST((G_A)_η, w)  $\cup$  F

В приведенном выше ( GA _в ) _η супервершин (путем рассмотрения вершин в несвязном компоненте как одно) и ребер A. — это подграф, состоящий из

Время работы

Алгоритм работает за время O ( E ), где E — количество ребер. Эта граница достигается следующим образом:

разделение на два набора с алгоритмами поиска медианы за O ( E )
найти лес в O ( E )
учитывая полуребра в E на каждой итерации O ( E + E /2 + E /4 + ··· + 1) = O ( E )

Пример

В следующем примере зеленые края используются для формирования MBST, а пунктирные красные области обозначают супервершины, сформированные на этапах алгоритма.

	Алгоритм наполовину делит ребра на два множества по весам. Зеленые ребра — это те ребра, вес которых как можно меньше.
	Поскольку в подграфе имеется остовное дерево, состоящее исключительно из ребер из меньшего множества ребер. Повторите поиск MBST в этом подграфе.
	Поскольку в текущем подграфе нет остовного дерева, сформированного из ребер из текущего набора меньших ребер. Объедините вершины несвязного компонента с супервершиной (обозначенной пунктирной красной областью), а затем найдите MBST в подграфе, образованном супервершинами и ребрами в большем наборе ребер. Лес, сформированный внутри каждого несвязного компонента, будет частью MBST в исходном графе.
	Повторите аналогичные шаги, объединив больше вершин в супервершину.
	В конечном итоге алгоритм получает MBST, используя ребра, найденные в ходе алгоритма.

Алгоритмы MBSA для ориентированных графов

Для ориентированного графа доступны два алгоритма: алгоритм Камерини для поиска MBSA и еще один от Габоу и Тарьяна. ^[4]

Алгоритм Камерини для MBSA

Для ориентированного графа алгоритм Камерини фокусируется на поиске набора ребер, максимальная стоимость которого будет равна стоимости узкого места MBSA. Это делается путем разделения набора ребер E на два набора A и B и сохранения набора T , который является набором, в котором известно, что G _T не имеет охватывающей древовидности, увеличивая T на B всякий раз, когда максимальная древовидность G ( B ∪ T ) не является остовным древовидием группы G , иначе мы уменьшим E на A . Общая временная сложность равна O ( E log E ). ^[5]^[4]

Псевдокод

function MBSA(G, w, T) is
    E ← the set of edges of G 
    if | E − T | > 1 then
        A ← UH(E-T)
        B ← (E − T) − A
        F ← BUSH(G_BUT)
        if F is a spanning arborescence of G then
            S ← F
            MBSA((G_BUT), w, T)
        else
            MBSA(G, w, TUB);

T представляет собой подмножество E, для которого известно, что GT _не содержит какой-либо связующей древовидности с корнем в узле «a». Первоначально T пусто
UH берет (E−T) набор ребер в G и возвращает A ⊂ (E−T) такой, что:
1. $|A|=\left\lfloor {\frac {(|E-T|)}{2}}\right\rfloor$
2. W _a ≥ W _b , для a ∈ A и b ∈ B
BUSH(G) возвращает максимальное разветвление G с корнем в узле «a».
Конечный результат будет S.

Пример

	После запуска первой итерации этого алгоритма мы получаем $F$ и $F$ не является остовным деревом $G.$ Поэтому мы запускаем код ⁠ $MBSA(G,w,T\cup B).$ ⁠
	Во второй итерации мы получаем $F'$ и $F'$ также не является связующим ветвлением $G.$ Поэтому мы запускаем код $MBSA(G,w,T'\cup B')$
	На третьей итерации мы получаем $F''$ и $F''$ является охватывающим деревом $G.$ Итак, мы запускаем код $MBSA(G_{T''\cup B''},w,T'')$
	когда мы запускаем $MBSA(G_{T''\cup B''},w,T'')$ , $\|E-T\|$ равно 1, что не больше 1, поэтому алгоритм возвращает результат и конечный результат $S=F''$ .

Алгоритм Габоу и Тарьяна для MBSA

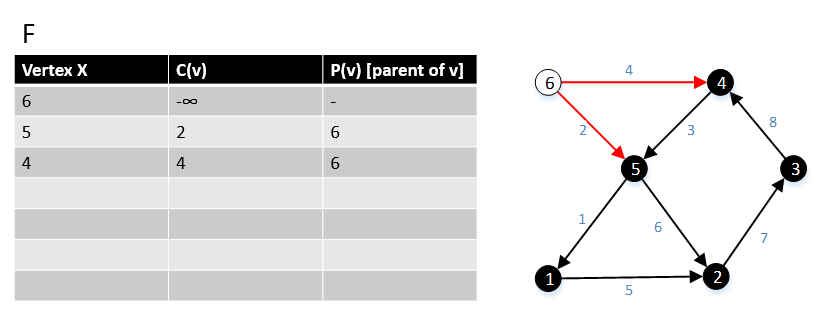
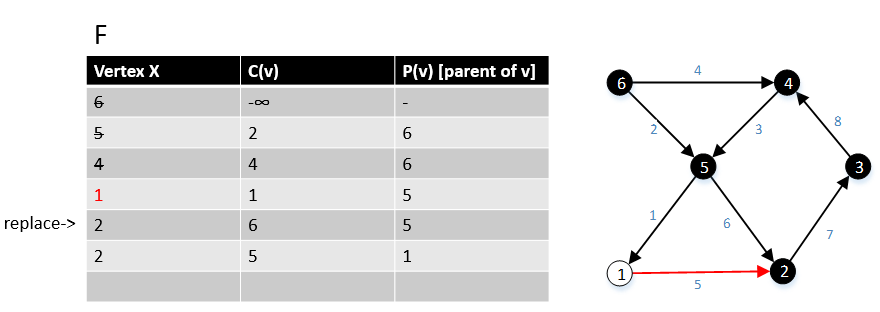
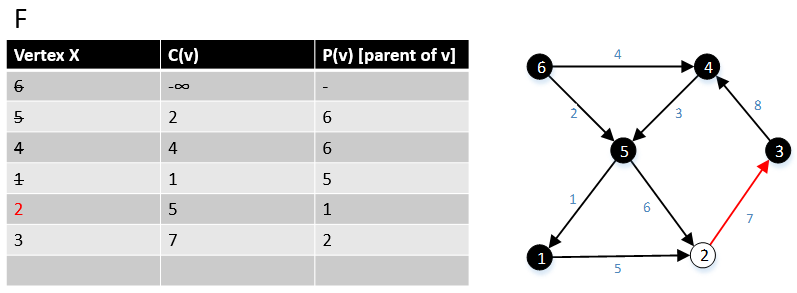
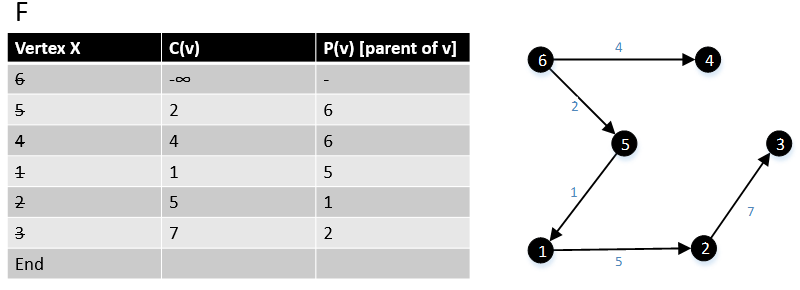
Габоу и Тарьян представили модификацию алгоритма Дейкстры для определения кратчайшего пути с одним источником, который создает MBSA. Их алгоритм работает за время O ( E + V log V ), если используется куча Фибоначчи . ^[7]

Псевдокод

 For a graph G(V,E), F is a collection of vertices in V. 
 Initially, F = {s} where s is the starting point of the graph G and c(s) = -∞

 1  function MBSA-GT(G, w, T)
 2      repeat |V| times
 3          Select v with minimum c(v) from F; 
 4          Delete it from the F;
 5          for ∀ edge(v, w) do
 6              if w ∉ F or ∉ Tree then
 7                  add w to F;          
 8                  c(w) = c(v,w);
 9                  p(w) = v;     
 10             else
 11                 if w ∈ F and c(w) > c(v, w) then
 12                     c(w) = c(v, w);
 13                     p(w) = v;

Пример

Следующий пример показывает, как работает алгоритм.

На первом шаге алгоритма мы выбираем корень s из графа G, на рисунке выше вершина 6 — это корень s. Затем мы нашли все ребра(6,w) € E и их стоимость c(6,w), где w € V.

Далее переходим в вершину 5 графа G, находим все ребра(5,w) € E и их стоимость c(5,w), где w € V.

Далее переходим в вершину 4 графа G, находим все ребра(4,w) ∈ E и их стоимость c(4,w), где w ∈ V. Находим, что ребро(4,5) > ребро(6.5), поэтому мы сохраняем ребро(6,5) и удаляем ребро(4,5).

Далее переходим в вершину 1 графа G, находим все ребра(1,w) ∈ E и их стоимость c(1,w), где w ∈ V. Находим, что ребро(5,2) > край(1,2), поэтому мы удаляем край(5,2) и сохраняем край(1,2).

Далее переходим в вершину 2 графа G, находим все ребра(2,w) € E и их стоимость c(2,w), где w € V.

Далее переходим в вершину 3 графа G, находим все ребра(3,w) ∈ E и их стоимость c(3,w), где w ∈ V. Находим, что ребро(3,4) > ребро(6,4), поэтому мы удалим ребро(3,4) и оставим ребро(6,4).

После того, как мы пройдемся по всем вершинам графа G, алгоритм завершится.

Другой подход, предложенный Тарьяном и Габоу, с границей $O (E log * V)$ для разреженных графов, в котором он очень похож на алгоритм Камерини для MBSA, но вместо разделения набора ребер на два набора на каждую итерацию $был введен K (i)$ , в котором i - количество разбиений, которые потребовали место или, другими словами, номер итерации, а $K (i)$ — возрастающая функция, обозначающая количество разделенных наборов, которые должны быть на итерацию. $К (я) знак равно 2 к (я - 1)$ с $k (1) = 2$ . Алгоритм находит $λ *$ где это значение края узкого места в любом MBSA. После $λ *$ находится любое остовное дерево в $G (λ *)$ — это MBSA, в котором $G (λ *)$ — это граф, стоимость всех ребер которого $\leq λ *$ . ^[4]^[7]

Ссылки

^ Все о связующем дереве узких мест
^ Мурали, Т.М. (2009), Применение минимальных остовных деревьев (PDF)
^ в вопросе 3 у вас есть доказательство этого утверждения (PDF)
^ Jump up to: ^а ^б ^с ^д ^и Трабулси, Ахмад (2014), связующие деревья узких мест (PDF) , заархивировано из оригинала (PDF) 4 марта 2016 г. , получено 28 декабря 2014 г.
^ Jump up to: ^а ^б Камерини, П.М. (1978), «Проблема связующего дерева мин-макс и некоторые расширения», Information Processing Letters , 7 (1): 10, doi : 10.1016/0020-0190(78)90030-3
^ Цуй, Юйсян (2013), Минимальное связующее дерево с узкими местами (PDF) , заархивировано из оригинала (PDF) 4 марта 2016 г. , получено 28 декабря 2014 г.
^ Jump up to: ^а ^б Габоу, Гарольд Н ; Тарьян, Роберт Э (1988). «Алгоритмы решения двух задач оптимизации узких мест» . Журнал алгоритмов . 9 (3): 411–417. дои : 10.1016/0196-6774(88)90031-4 . ISSN 0196-6774 .

[1] Все о связующем дереве узких мест

[2] Мурали, Т.М. (2009), Применение минимальных остовных деревьев (PDF)

[3] в вопросе 3 у вас есть доказательство этого утверждения (PDF)

[Traboulsi2014-4] Jump up to: ^а ^б ^с ^д ^и Трабулси, Ахмад (2014), связующие деревья узких мест (PDF) , заархивировано из оригинала (PDF) 4 марта 2016 г. , получено 28 декабря 2014 г.

[Camerini1978-5] Jump up to: ^а ^б Камерини, П.М. (1978), «Проблема связующего дерева мин-макс и некоторые расширения», Information Processing Letters , 7 (1): 10, doi : 10.1016/0020-0190(78)90030-3

[6] Цуй, Юйсян (2013), Минимальное связующее дерево с узкими местами (PDF) , заархивировано из оригинала (PDF) 4 марта 2016 г. , получено 28 декабря 2014 г.

[GabowTarjan1988-7] Jump up to: ^а ^б Габоу, Гарольд Н ; Тарьян, Роберт Э (1988). «Алгоритмы решения двух задач оптимизации узких мест» . Журнал алгоритмов . 9 (3): 411–417. дои : 10.1016/0196-6774(88)90031-4 . ISSN 0196-6774 .

[1]

[2]

[3]

[4]

[5]

[6]

[7]