Анализ достижимости

Анализ достижимости — это решение проблемы достижимости в конкретном контексте распределенных систем. Он используется для определения того, какие глобальные состояния могут быть достигнуты распределенной системой, состоящей из определенного количества локальных объектов, которые обмениваются сообщениями.

Обзор [ править ]

Анализ достижимости был представлен в статье 1978 года для анализа и проверки протоколов связи . ^[1] Эта статья была вдохновлена статьей Бартлетта и др. 1968 года ^[2] который представил протокол альтернативных битов с использованием конечного моделирования объектов протокола, а также указал, что аналогичный протокол, описанный ранее, имел конструктивный недостаток. Этот протокол принадлежит канальному уровню и при определенных предположениях обеспечивает правильную доставку данных без потерь и дублирования, несмотря на случайное повреждение или потерю сообщения.

Для анализа достижимости локальные объекты моделируются по их состояниям и переходам. Объект меняет состояние, когда он отправляет сообщение, потребляет полученное сообщение или выполняет взаимодействие на своем локальном интерфейсе службы. Глобальное состояние $s=(s_{1},s_{2},...,s_{n},medium)$ системы с n сущностями ^[3] определяется штатами $s_{i}$ (i=1, ... n) сущностей и состояние связи $medium$ . В простейшем случае среда между двумя объектами моделируется двумя очередями FIFO в противоположных направлениях, которые содержат сообщения в пути (которые отправлены, но еще не потреблены). Анализ достижимости рассматривает возможное поведение распределенной системы путем анализа всех возможных последовательностей переходов состояний сущностей и соответствующих достигнутых глобальных состояний. ^[4]

Результатом анализа достижимости является глобальный граф перехода состояний (также называемый графом достижимости), который показывает все глобальные состояния распределенной системы, достижимые из исходного глобального состояния, а также все возможные последовательности взаимодействий отправки, потребления и обслуживания, выполняемые локальным сущности. Однако во многих случаях этот граф переходов неограничен и не может быть исследован полностью. Граф переходов можно использовать для проверки общих недостатков проектирования протокола (см. ниже), а также для проверки того, что последовательности сервисных взаимодействий объектов соответствуют требованиям, заданным глобальной сервисной спецификацией системы. ^[1]

Свойства протокола [ править ]

Ограниченность: глобальный граф переходов состояний ограничен, если ограничено количество сообщений, которые могут находиться в пути, и ограничено количество состояний всех объектов. Вопрос о том, остается ли число сообщений ограниченным в случае конечных государственных объектов, вообще говоря, неразрешим . ^[5] Обычно исследование графа переходов прекращается, когда количество сообщений в пути достигает заданного порога.

К конструктивным недостаткам относятся следующие:

Глобальный тупик: система находится в глобальном тупике, если все объекты ждут приема сообщения и ни одно сообщение не находится в пути. Отсутствие глобальных взаимоблокировок можно проверить, проверив, что ни одно состояние в графе достижимости не является глобальным взаимоблокировкой.
Частичные взаимоблокировки: объект находится в тупиковом состоянии, если он ожидает потребления сообщения, а система находится в глобальном состоянии, где такое сообщение не находится в пути и никогда не будет отправлено в любом глобальном состоянии, которое может быть достигнуто в будущее. Такое нелокальное свойство можно проверить, выполнив проверку модели на графе достижимости.
Неопределенный прием: объект имеет неопределенный прием, если следующее сообщение, которое будет использовано, не ожидается спецификацией поведения объекта в его текущем состоянии. Отсутствие этого условия можно проверить, проверив все состояния графа достижимости.

Пример [ править ]

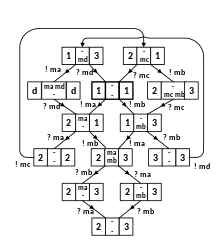
В качестве примера мы рассматриваем систему двух протокольных объектов, которые обмениваются сообщениями ma , mb , mc и md друг с другом, как показано на первой диаграмме. Протокол определяется поведением двух сущностей, которое представлено на второй диаграмме в виде двух конечных автоматов. Здесь символ "!" означает отправку сообщения, а "?" означает потребление полученного сообщения. Начальными состояниями являются состояния «1».

Третья диаграмма показывает результат анализа достижимости этого протокола в виде глобального конечного автомата. Каждое глобальное состояние имеет четыре компонента: состояние объекта протокола A (слева), состояние объекта B (справа) и сообщения, находящиеся в пути в середине (верхняя часть: от A к B; нижняя часть: от B к A). ). Каждый переход этого глобального конечного автомата соответствует одному переходу объекта протокола A или объекта B. Начальное состояние — [1, - -, 1] (нет сообщений в пути).

Видно, что этот пример имеет ограниченное глобальное пространство состояний — максимальное количество сообщений, которые могут находиться в пути одновременно, равно двум. Этот протокол имеет глобальную тупиковую ситуацию, которая представляет собой состояние [2, - -, 3]. Если удалить переход A в состояние 2 для потребления сообщения mb , произойдет неопределенный прием в глобальных состояниях [2, ma mb ,3] и [2, - mb ,3].

Передача сообщения [ править ]

Конструкция протокола должна быть адаптирована к свойствам базовой среды связи, к возможности сбоя партнера по связи и к механизму, используемому объектом для выбора следующего сообщения для потребления. Среда связи для протоколов на канальном уровне обычно ненадежна и допускает ошибочный прием и потерю сообщений (моделируется как переход состояния среды). Протоколы, использующие службу IP Интернета, также должны учитывать возможность доставки вне очереди. Протоколы более высокого уровня обычно используют сеансово-ориентированную транспортную службу, что означает, что среда обеспечивает надежную передачу сообщений FIFO между любой парой объектов. Однако при анализе распределенных алгоритмов часто принимают во внимание возможность полного отказа какого-либо объекта, что обычно обнаруживается (например, потеря сообщения в среде) механизмом таймаута , когда ожидаемое сообщение не приходит.

Были сделаны различные предположения о том, может ли организация выбрать конкретное сообщение для потребления, когда несколько сообщений прибыли и готовы к использованию. Базовые модели следующие:

Единая входная очередь: у каждого объекта есть одна очередь FIFO, в которой входящие сообщения хранятся до тех пор, пока они не будут использованы. Здесь объект не имеет права выбора и должен использовать первое сообщение в очереди.
Несколько очередей: каждый объект имеет несколько очередей FIFO, по одной для каждого взаимодействующего партнера. Здесь сущность имеет возможность решить, в зависимости от своего состояния, из какой очереди (или очередей) должно быть использовано следующее входное сообщение.
Пул приема: у каждого объекта есть один пул, в котором полученные сообщения хранятся до тех пор, пока они не будут использованы. Здесь сущность имеет право решать, в зависимости от своего состояния, какой тип сообщения должен быть использован следующим (и ждать сообщения, если оно еще не получено) или, возможно, использовать одно из набора типов сообщений (чтобы рассматривать альтернативы).

Оригинальная статья, раскрывающая проблему неопределенных приемов, ^[6] и большая часть последующей работы предполагала единственную входную очередь. ^[7] Иногда неуказанные приемы вводятся условием гонки , что означает, что принимаются два сообщения и их порядок не определен (что часто бывает, если они приходят от разных партнеров). Многие из этих недостатков проектирования исчезают при использовании нескольких очередей или пулов приема. ^[8] При систематическом использовании пулов приема анализ достижимости должен проверять наличие частичных взаимоблокировок и сообщений, остающихся навсегда в пуле (без использования объектом). ^[9]

Практические вопросы [ править ]

В большинстве работ по моделированию протоколов используются конечные автоматы (FSM) для моделирования поведения распределенных объектов (см. также «Взаимодействие с конечными автоматами» ). Однако эта модель недостаточно мощна для моделирования параметров сообщения и локальных переменных. Поэтому часто используются так называемые расширенные модели конечных автоматов, например, поддерживаемые такими языками, как SDL или конечные автоматы UML . К сожалению, для таких моделей анализ достижимости становится намного сложнее.

Практической проблемой анализа достижимости является так называемый «взрыв пространства состояний». Если два объекта протокола имеют по 100 состояний каждый, а среда может включать 10 типов сообщений, до двух в каждом направлении, то количество глобальных состояний в графе достижимости ограничивается числом 100 x 100 x (10 х 10) х (10 х 10), что составляет 100 миллионов. Поэтому был разработан ряд инструментов для автоматического выполнения анализа достижимости и проверки модели на графе достижимости. Упомянем лишь два примера: средство проверки моделей SPIN и набор инструментов для построения и анализа распределенных процессов .

Дальнейшее чтение [ править ]

Протоколы связи
Джеральд Хольцманн: Проектирование и проверка компьютерных протоколов , Прентис Холл , 1991.
Г. В. Бохманн, Д. Рейнер и Ч. Уэст: Некоторые заметки по истории разработки протоколов, журнал Computer Networks, 54 (2010), стр. 3197–3209.

Ссылки и примечания [ править ]

^ Jump up to: Перейти обратно: ^а ^б Бохманн, Г.В. «Описание протоколов связи в конечных состояниях, компьютерные сети, том 2 (1978), стр. 361–372». {{cite journal}}: Для цитирования журнала требуется |journal= ( помощь )
^ К. А. Бартлетт, Р. А. Скантлбери и П. Т. Уилкинсон, Заметка о надежной полнодуплексной передаче по полудуплексным каналам, C.ACM 12, 260 (1969).
^ Примечание. В случае анализа протокола обычно существует только два объекта.
^ Примечание. Повреждение или потеря сообщения моделируется как переход состояния $medium$ .
^ М.Г.Гуда, Э.Г.Маннинг, Ю.Т.Ю.: О ходе связи между двумя конечными автоматами, doi
^ П. Зафиропуло, К. Уэст, Х. Рудин, Д. Коуэн, Д. Брэнд: На пути к анализу и синтезу протоколов, Транзакции IEEE в коммуникациях (Том: 28, Выпуск: 4, апрель 1980 г.)
^ Примечание. Конструкция SAVE SDL может использоваться для указания того, что определенные типы сообщений не должны использоваться в текущем состоянии, а должны сохраняться для будущей обработки.
^ М.Ф. Аль-Хаммури и Г.В. Бохманн: Реализуемость спецификаций услуг, Proc. Конференция по системному анализу и моделированию (SAM) 2018, Копенгаген, LNCS, Springer
^ К. Фурне, Т. Хоар, С. К. Раджамани и Дж. Рехоф: Соответствие без заеданий, Proc. 16-й международный Конф. по компьютерной верификации (CAV'04), LNCS, vol. 3114, Спрингер, 2004 г.

[Boch78-1] Jump up to: Перейти обратно: ^а ^б Бохманн, Г.В. «Описание протоколов связи в конечных состояниях, компьютерные сети, том 2 (1978), стр. 361–372». {{cite journal}}: Для цитирования журнала требуется |journal= ( помощь )

[2] К. А. Бартлетт, Р. А. Скантлбери и П. Т. Уилкинсон, Заметка о надежной полнодуплексной передаче по полудуплексным каналам, C.ACM 12, 260 (1969).

[3] Примечание. В случае анализа протокола обычно существует только два объекта.

[4] Примечание. Повреждение или потеря сообщения моделируется как переход состояния $medium$ .

[5] М.Г.Гуда, Э.Г.Маннинг, Ю.Т.Ю.: О ходе связи между двумя конечными автоматами, doi

[6] П. Зафиропуло, К. Уэст, Х. Рудин, Д. Коуэн, Д. Брэнд: На пути к анализу и синтезу протоколов, Транзакции IEEE в коммуникациях (Том: 28, Выпуск: 4, апрель 1980 г.)

[7] Примечание. Конструкция SAVE SDL может использоваться для указания того, что определенные типы сообщений не должны использоваться в текущем состоянии, а должны сохраняться для будущей обработки.

[8] М.Ф. Аль-Хаммури и Г.В. Бохманн: Реализуемость спецификаций услуг, Proc. Конференция по системному анализу и моделированию (SAM) 2018, Копенгаген, LNCS, Springer

[9] К. Фурне, Т. Хоар, С. К. Раджамани и Дж. Рехоф: Соответствие без заеданий, Proc. 16-й международный Конф. по компьютерной верификации (CAV'04), LNCS, vol. 3114, Спрингер, 2004 г.

[1]

[2]

[3]

[4]

[5]

[6]

[7]

[8]

[9]