Удушенный граф
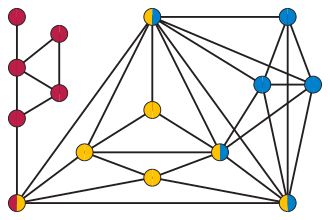
В математике теории графов — удушенный граф это граф , в котором удаление ребер любого индуцированного цикла длиной больше трех приведет к отключению оставшегося графа. То есть это графы, в которых каждый периферийный цикл представляет собой треугольник.
Примеры
[ редактировать ]В максимальном планарном графе или, в более общем смысле, в каждом многогранном графе периферийные циклы являются в точности гранями плоского вложения графа, поэтому многогранный граф является удушенным тогда и только тогда, когда все грани являются треугольниками, или, что то же самое, он максимален. плоский. Каждый хордальный граф удушается, поскольку единственными индуцированными циклами в хордальных графах являются треугольники, поэтому больше нет циклов, которые можно было бы удалить.
Характеристика
[ редактировать ]Клика -сумма двух графов формируется путем идентификации двух клик одинакового размера в каждом графе и последующего удаления некоторых ребер клики. Для версии клик-сумм, соответствующей удушенным графам, шаг удаления ребер опущен. Клика-сумма этого типа между двумя защемленными графами приводит к получению другого защемленного графа, поскольку каждый длинный индуцированный цикл в сумме должен быть ограничен той или иной стороной (иначе у него была бы хорда между вершинами, в которых он пересекал один сторона суммы к другой), а несвязные части этой стороны, образовавшиеся в результате удаления цикла, должны оставаться несвязными в клик-сумме. Таким образом, каждый хордальный граф можно разложить в клик-сумму полных графов , а каждый максимальный планарный граф можно разложить в клик-сумму 4-связных максимальных планарных графов.
Как показывают Сеймур и Уивер (1984) , это единственные возможные строительные блоки ущемленных графов: ущемленные графы — это именно те графы, которые могут быть сформированы как кликовые суммы полных графов и максимальных планарных графов.
См. также
[ редактировать ]- Линейный совершенный граф — граф, в котором каждый нечетный цикл представляет собой треугольник.
Ссылки
[ редактировать ]- Сеймур, Полиция ; Уивер, Р.В. (1984), «Обобщение хордальных графов», Журнал теории графов , 8 (2): 241–251, doi : 10.1002/jgt.3190080206 , MR 0742878 .