Арифметический бильярд

В развлекательной математике арифметический бильярд представляет собой геометрический метод определения наименьшего общего кратного и наибольшего общего делителя двух натуральных чисел с использованием отражений внутри прямоугольника, стороны которого представляют собой два заданных числа. Это простой пример траекторного анализа динамического бильярда .

Хьюго Штейнхаус рассматривал арифметический бильярд как математические головоломки. ^[1] и Мартин Гарднер , ^[2] и известны учителям математики под названием «Paper Pool». ^[3]Они использовались в качестве источника вопросов в математических кругах. ^[4]

Арифметическая бильярдная дорожка

Арифметический бильярд для чисел 10 и 40.

Рассмотрим прямоугольник с целыми сторонами и построим путь внутри этого прямоугольника следующим образом:

начните с угла и двигайтесь по прямой, составляющей угол 45° с сторонами;
каждый раз, когда путь сталкивается с стороной, отражайте его под одним и тем же углом (путь делает поворот на 90° влево или вправо);
в конце концов (т.е. после конечного числа отражений) путь достигает угла и там останавливается.

Если длина одной стороны делит другую, путь представляет собой зигзаг, состоящий из одного или нескольких сегментов.В противном случае путь имеет самопересечения и состоит из отрезков различной длины в двух ортогональных направлениях.В общем случае путь представляет собой пересечение прямоугольника с сеткой квадратов (ориентированной под углом 45° относительно сторон прямоугольника).

Арифметические особенности пути

Арифметический бильярд для чисел 3 и 8. — Арифметический бильярд для чисел 3 и 8: наибольший общий делитель — 1, наименьшее общее кратное — 24.

Вызов $a$ и $b$ длины сторон прямоугольника и разделите их на $a\cdot b$ единичные квадраты. Наименьшее общее кратное $\operatorname {lcm} (a,b)$ - это количество единичных квадратов, пересекаемых арифметической бильярдной дорожкой, или, что то же самое, длина пути, деленная на ${\sqrt {2}}$ . В частности, путь проходит через каждый единичный квадрат тогда и только тогда, когда $a$ и $b$ взаимнопросты .

Предположим, что ни одна из двух сторон не делит другую. Тогда первый отрезок арифметической бильярдной дорожки содержит точку самопересечения, ближайшую к начальной точке. Наибольший общий делитель $\gcd(a,b)$ - это количество единичных квадратов, пересекаемых первым сегментом пути до этой точки самопересечения.

Количество точек отскока арифметической бильярдной дорожки по двум сторонам длины $a$ равно $(a/\operatorname {gcd} (a,b))-1$ и аналогично $(b/\operatorname {gcd} (a,b))-1$ для двух сторон длины $b$ . В частности, если $a$ и $b$ взаимно простые, то общее количество точек контакта между траекторией и периметром прямоугольника (т. е. точки отскока плюс начальный и конечный угол) равно $a+b$ .

Конечный угол пути противоположен начальному углу тогда и только тогда, когда $a$ и $b$ делятся в точности на одну и ту же степень двойки (например, если они оба нечетны), иначе это один из двух соседних углов, в зависимости от того, является ли $a$ или $b$ имеет больше факторов $2$ в его первичной факторизации .

Путь симметричен : если начальный и конечный углы противоположны, то путь точечно-симметричен относительно центра прямоугольника, в противном случае он симметричен относительно биссектрисы стороны, соединяющей начальный и конечный угол.

Точки контакта между арифметической бильярдной дорожкой и периметром прямоугольника распределены равномерно: расстояние по периметру (т.е. возможно заходя за угол) между двумя такими соседними точками равно $2\gcd(a,b)$ .

Установите координаты в прямоугольнике так, чтобы начальная точка была $(0,0)$ и противоположный угол $(a,b)$ . Тогда любая точка арифметического биллиарда, имеющая целочисленные координаты, обладает свойством четности суммы координат (четность не может меняться при движении по диагоналям единичных квадратов). Точки самопересечения пути, точки отскока, а также начальный и конечный угол — это в точности точки прямоугольника, координаты которых кратны $\gcd(a,b)$ и такая, что сумма координат является четным кратным $\gcd(a,b)$ .

Идеи доказательства

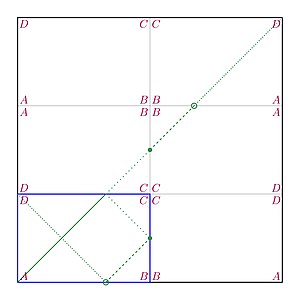
Отражение бильярда. — Отражая бильярд, мы можем представить путь как прямую линию. В этом примере соотношение двух данных чисел равно 2/3.

Отражая бильярд: рассмотрим квадрат со стороной $\operatorname {lcm} (a,b)$ . Отображая несколько копий исходного прямоугольника (с зеркальной симметрией), мы можем визуализировать арифметическую бильярдную дорожку как диагональ этого квадрата. Другими словами, мы можем подумать об отражении прямоугольника, а не сегментов пути.

Приведение к взаимно простому случаю: удобно изменить масштаб прямоугольника, делящего $a$ и $b$ по их наибольшему общему делителю, операция, которая не меняет геометрию пути (например, количество точек отражения).

Изменение времени: движение пути «обратимо во времени», что означает, что если путь в данный момент пересекает один конкретный единичный квадрат(в определенном направлении), то нет абсолютно никаких сомнений, из какой единицы квадрата и с какой стороны он только что пришел. ^[4]

Доказательство можно найти в популяризационной статье. ^[5]

Одно обобщение

ВСЕ. — Периодический путь в обобщенном арифметическом биллиарде со сторонами 35 и 14.

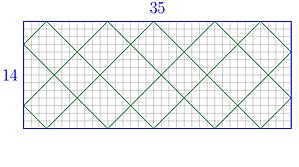
Если мы позволим начальной точке пути быть любой точкой прямоугольника с целочисленными координатами, то существуют также периодические пути, если только стороны прямоугольника не взаимно просты. Длина любого периодического пути равна $2\operatorname {lcm} (a,b)\cdot {\sqrt {2}}$ .

Ссылки

^ Штайнхаус, Хьюго (1999). Математические снимки (изд. Dover Recreational Math Series). Курьерская корпорация. п. 63. ИСБН 0486409147 .
^ Гарднер, Мартин (1984). Шестая книга математических развлечений из «Scientific American» . Издательство Чикагского университета. стр. 211–215. ISBN 0226282503 .
^ «Игра в бумажный пул» . NCTM Просветление . Национальный совет учителей математики . Проверено 10 января 2018 г.
^ Jump up to: ^а ^б Тантон, Джеймс (2012). Математическое изобилие! Первые пять лет существования Математического института Святого Марка . Математическая ассоциация Америки. стр. 145–156. ISBN 978-0883857762 .
^ Перукка, Антонелла (24 апреля 2018 г.). «Арифметический бильярд» . Плюс журнал . Кембриджский университет . Проверено 23 декабря 2018 г.

[Steinhaus-1] Штайнхаус, Хьюго (1999). Математические снимки (изд. Dover Recreational Math Series). Курьерская корпорация. п. 63. ИСБН 0486409147 .

[Gardner-2] Гарднер, Мартин (1984). Шестая книга математических развлечений из «Scientific American» . Издательство Чикагского университета. стр. 211–215. ISBN 0226282503 .

[NCTM-3] «Игра в бумажный пул» . NCTM Просветление . Национальный совет учителей математики . Проверено 10 января 2018 г.

[Tanton-4] Jump up to: ^а ^б Тантон, Джеймс (2012). Математическое изобилие! Первые пять лет существования Математического института Святого Марка . Математическая ассоциация Америки. стр. 145–156. ISBN 978-0883857762 .

[Perucca-5] Перукка, Антонелла (24 апреля 2018 г.). «Арифметический бильярд» . Плюс журнал . Кембриджский университет . Проверено 23 декабря 2018 г.

[1]

[2]

[3]

[4]

[5]