Проблема максимального потока

Сеть потоков для решения проблемы: каждый человек (r i ) готов взять кошку (wi 1 ) и/или собаку (wi 2 ). Однако каждое домашнее животное (pi ) отдает предпочтение только определенной части людей. Найдите любое совпадение домашних животных с людьми, при котором максимальное количество домашних животных будет усыновлено одним из предпочитаемых им людей.

В теории оптимизации задачи максимального потока включают в себя поиск допустимого потока через сеть потоков , который обеспечивает максимально возможную скорость потока.

Задачу максимального потока можно рассматривать как частный случай более сложных задач сетевого потока, таких как задача циркуляции . Максимальное значение st-потока (т. е. потока от источника s к стоку t) равно минимальной пропускной способности st-отреза (т. е. отреза, отделяющего s от t) в сети, как указано в минимальном потоке max-flow. теорема о разрезе .

История

Проблема максимального потока была впервые сформулирована в 1954 году Т.Э. Харрисом и Ф.С. Россом как упрощенная модель советского железнодорожного потока.

В 1955 году Лестер Р. Форд-младший и Делберт Р. Фулкерсон создали первый известный алгоритм — алгоритм Форда-Фалкерсона . В своей статье 1955 г. Форд и Фулкерсон писали, что проблема Харриса и Росса формулируется следующим образом (см. п. 5):

Рассмотрим железнодорожную сеть, соединяющую два города через ряд промежуточных городов, где каждому звену сети присвоен номер, обозначающий его пропускную способность. Допустив установившееся состояние, найдите максимальный поток из одного города в другой.

В своей книге «Потоки в сети » в 1962 году Форд и Фулкерсон писали:

Она была поставлена ​​перед авторами весной 1955 года Т.Э. Харрисом, который совместно с генералом Ф.С. Россом (в отставке) сформулировал упрощенную модель железнодорожного движения и определил эту конкретную проблему как центральную, предложенную модель [11].

где [11] относится к секретному отчету «Основы метода оценки пропускной способности железнодорожных сетей» 1955 года. Харриса и Росса (видеть п. 5).

С годами были обнаружены различные улучшенные решения проблемы максимального потока, в частности, алгоритм кратчайшего увеличивающего пути Эдмондса и Карпа и независимо Диница; алгоритм блокирующего потока Диница; алгоритм push - Голдберга Тарьяна и ; relabel и алгоритм потока двоичной блокировки Голдберга и Рао. Алгоритмы Шермана и Келнер, Ли, Ореккья и Сидфорд, соответственно, найти приблизительно оптимальный максимальный поток, но работать только на неориентированных графах.

В 2013 году Джеймс Б. Орлин опубликовал статью, описывающую $O(|V||E|)$ алгоритм.

В 2022 году Ли Чен, Расмус Кинг, Ян П. Лю, Ричард Пэн, Максимилиан Пробст Гутенберг и Сушант Сачдева опубликовали алгоритм почти линейного времени, работающий в $O(|E|^{1+o(1)})$ для задачи о потоке с минимальной стоимостью , частным случаем которой является задача о максимальном потоке. Для задачи о кратчайшем пути с одним источником (SSSP) с отрицательными весами также был описан еще один частный случай задачи о потоке с минимальной стоимостью, алгоритм которого работает почти за линейное время. Оба алгоритма были признаны лучшими докладами на Симпозиуме по основам компьютерных наук 2022 года .

Определение

Сеть потоков с источником s и стоком t . Цифры рядом с краями — это емкости.

Сначала установим некоторые обозначения:

• Позволять $N=(V,E)$ быть сетью с $s,t\in V$ являясь источником и стоком $N$ соответственно.
• Если $g$ есть функция на ребрах $N$ тогда его значение на $(u,v)\in E$ обозначается $g_{uv}$ или $g(u,v).$

Определение. ребра Пропускная способность — это максимальный объем потока, который может пройти через ребро. Формально это карта $c:E\to \mathbb {R} ^{+}.$

Определение. Поток — это карта $f:E\to \mathbb {R}$ который удовлетворяет следующему:

• Ограничение мощности . Поток ребра не может превышать его пропускную способность, другими словами: $f_{uv}\leq c_{uv}$ для всех $(u,v)\in E.$
• Сохранение потоков. Сумма потоков, входящих в узел, должна равняться сумме потоков, выходящих из этого узла, за исключением источника и приемника. Или:

$\forall v\in V\setminus \{s,t\}:\quad \sum _{u:(u,v)\in E,f_{uv}>0}f_{uv}=\sum _{u:(v,u)\in E,f_{vu}>0}f_{vu}.$

Замечание . Потоки кососимметричны: $f_{uv}=-f_{vu}$ для всех $(u,v)\in E.$

Определение. Величина потока – это количество потока, проходящего от источника к стоку. Формально для потока $f:E\to \mathbb {R} ^{+}$ это дается:

$|f|=\sum _{v:\ (s,v)\in E}f_{sv}=\sum _{u:\ (u,t)\in E}f_{ut}.$

Определение. Задача о максимальном потоке состоит в том, чтобы направить как можно больший поток от источника к стоку, другими словами, найти поток. $f_{\textrm {max}}$ с максимальным значением.

Обратите внимание, что может существовать несколько максимальных потоков, и если допускаются произвольные действительные (или даже произвольные рациональные) значения потока (вместо целых чисел), существует либо ровно один максимальный поток, либо бесконечно много, поскольку существует бесконечно много линейных комбинаций потоков. базовый максимальный поток. Другими словами, если мы отправим $x$ единицы расхода на ребре $u$ в одном максимальном потоке, и $y>x$ единицы расхода на $u$ в другом максимальном потоке, то для каждого $\Delta \in [0,y-x]$ мы можем отправить $x+\Delta$ единицы на $u$ и соответствующим образом направить поток на оставшиеся ребра, чтобы получить еще один максимальный поток. Если значения потока могут быть любыми действительными или рациональными числами, то таких чисел бесконечно много. $\Delta$ значения для каждой пары $x,y$.

Алгоритмы

В следующей таблице перечислены алгоритмы решения задачи максимального расхода. Здесь, $V$ и $E$ обозначают количество вершин и ребер сети. Значение $U$ относится к наибольшей граничной мощности после масштабирования всех мощностей до целочисленных значений. (если сеть содержит иррациональные мощности, $U$ может быть бесконечным).

Метод	Год	Сложность	Описание
Линейное программирование			Ограничения, задаваемые определением юридического потока . См. линейную программу здесь.
Алгоритм Форда – Фулкерсона	1955	$O(EU)$	Пока существует открытый путь через остаточный граф, отправьте минимум остаточных мощностей по этому пути.
Алгоритм Эдмондса – Карпа	1970	$O(VE^{2})$	Специализация Форда-Фалкерсона, поиск дополнительных путей с помощью поиска в ширину .
Алгоритм Динича	1970	$O(V^{2}E)$	На каждом этапе алгоритм строит многоуровневый граф с поиском в ширину по остаточному графу . Максимальный поток в многоуровневом графе можно рассчитать в $O(VE)$ время, а максимальное количество фаз $V-1$. В сетях с единичной пропускной способностью алгоритм Динича завершается $O(\min\{V^{2/3},E^{1/2}\}E)$ время.
Алгоритм MKM (Малхотра, Кумар, Махешвари)	1978	$O(V^{3})$	Модификация алгоритма Динича с другим подходом к построению блокирующих потоков. Обратитесь к оригинальной статье .
Алгоритм Динича с динамическими деревьями	1983	$O(VE\log V)$	Структура данных динамических деревьев ускоряет вычисление максимального потока в многоуровневом графе. $O(VE\log V)$.
Общий алгоритм push-relabel	1986	$O(V^{2}E)$	Алгоритм push relabel поддерживает предпоток, т.е. функцию потока с возможностью превышения вершин. Алгоритм работает, пока в графе есть вершина с положительным эксцессом, т.е. активная вершина. Операция push увеличивает поток на остаточном ребре, а функция высоты вершин контролирует, через какие остаточные ребра можно проталкивать поток. Функция высоты изменяется в результате операции перемаркировки. Правильные определения этих операций гарантируют, что результирующая функция потока будет максимальным потоком.
Алгоритм push-relabel с FIFO правилом выбора вершин	1988	$O(V^{3})$	Вариант алгоритма push-relabel, который всегда выбирает самую последнюю активную вершину и выполняет операции push, пока избыток положителен и существуют допустимые остаточные ребра из этой вершины.
Алгоритм push-relabel с на максимальном расстоянии правилом выбора вершин	1988	$O(V^{2}{\sqrt {E}})$	Вариант алгоритма push-relabel, который всегда выбирает самую удаленную вершину из $s$ или $t$ (т.е. вершина самой высокой метки), но в остальном действует как алгоритм FIFO.
Алгоритм push-relabel с динамическими деревьями	1988	$O\left(VE\log {\frac {V^{2}}{E}}\right)$	Алгоритм строит деревья ограниченного размера на остаточном графе относительно функции высоты. Эти деревья обеспечивают многоуровневые операции перемещения, т. е. перемещение по всему пути насыщения, а не по одному ребру.
Алгоритм KRT (Кинг, Рао, Тарьян)	1994	$O\left(VE\log _{\frac {E}{V\log V}}V\right)$
Алгоритм двоичного потока блокировки	1998	$O\left(E\cdot \min\{V^{2/3},E^{1/2}\}\cdot \log {\frac {V^{2}}{E}}\cdot \log U\right)$
Алгоритм Джеймса Б. Орлина + KRT (Кинг, Рао, Тарьян)	2013	$O(VE)$	Алгоритм Орлина решает максимальный поток в $O(VE)$ время для $E\leq O(V^{{\frac {16}{15}}-\epsilon })$ в то время как KRT решает эту проблему в $O(VE)$ для $E>V^{1+\epsilon }$.
Алгоритм Катурии-Лю-Сидфорда	2020	$E^{4/3+o(1)}U^{1/3}$	Методы внутренних точек и усиление границ с использованием $\ell _{p}$-норм течет. Основан на более раннем алгоритме Madry, который достиг времени выполнения. ${\tilde {O}}(E^{10/7}U^{1/7})$.
Алгоритм BLNPSSSW/BLLSSSW	2020	${\tilde {O}}((E+V^{3/2})\log U)$	Методы внутренних точек и динамическое сопровождение электрических потоков с помощью детандерных разложений.
Алгоритм Гао-Лю-Пэна	2021	${\tilde {O}}(E^{{\frac {3}{2}}-{\frac {1}{328}}}\log U)$	Алгоритм Гао, Лю и Пэна вращается вокруг динамического поддержания увеличивающихся электрических потоков, лежащих в основе алгоритма, основанного на методе внутренней точки, из [Mądry JACM '16]. Это влечет за собой разработку структур данных, которые в ограниченных условиях возвращают ребра с большой электрической энергией на графе, подвергающемся обновлению сопротивления.
Алгоритм Чена, Кинга, Лю, Пэна, Гутенберга и Сачдевы	2022	$O(E^{1+o(1)}\log U)$ Точная сложность в статье четко не указана, но, по-видимому, $E\exp O(\log ^{7/8}E\log \log E)\log U$	Алгоритм Чена, Кинга, Лю, Пэна, Гутенберга и Сачдевы решает поток с максимальным потоком и потоком с минимальной стоимостью почти за линейное время, строя поток через последовательность $E^{1+o(1)}$ приблизительные ненаправленные циклы минимального соотношения, каждый из которых рассчитывается и обрабатывается в амортизированных $E^{o(1)}$ время с использованием динамической структуры данных.

Дополнительные алгоритмы см. в Goldberg & Tarjan (1988) .

Теорема об интегральном потоке

Теорема об интегральном потоке утверждает, что

Если каждое ребро потоковой сети имеет целую пропускную способность, то существует целый максимальный поток.

Утверждение заключается не только в том, что значение потока является целым числом, что следует непосредственно из теоремы о максимальном потоке и минимальном разрезе , но и в том, что поток на каждом ребре является целым. Это имеет решающее значение для многих комбинаторных приложений (см. ниже), где поток через ребро может кодировать, должен ли элемент, соответствующий этому ребру, быть включен в искомое множество или нет.

Приложение

Проблема максимального расхода с несколькими источниками и несколькими стоками

Рис. 4.1.1. Преобразование задачи о максимальном расходе с несколькими источниками и множеством стоков в задачу о максимальном расходе с одним источником и одним стоком

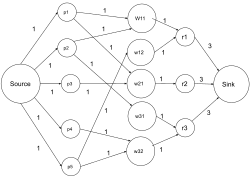
Учитывая сеть $N=(V,E)$ с набором исходников $S=\{s_{1},\ldots ,s_{n}\}$ и набор раковин $T=\{t_{1},\ldots ,t_{m}\}$ вместо одного источника и одного стока мы должны найти максимальный поток через $N$. Мы можем преобразовать задачу с несколькими источниками и множеством приемников в задачу о максимальном потоке, добавив консолидированный источник, соединяющийся с каждой вершиной в $S$ и объединенный сток, соединенный каждой вершиной в $T$ (также известный как суперисточник и суперприемник ) с бесконечной пропускной способностью на каждом ребре (см. рис. 4.1.1.).

Двустороннее сопоставление максимальной мощности

Рис. 4.3.1. Преобразование задачи о максимальном двудольном сопоставлении в задачу о максимальном потоке

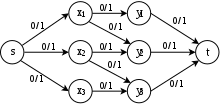
Учитывая двудольный граф $G=(X\cup Y,E)$, нам нужно найти паросочетание максимальной мощности в $G$, то есть паросочетание, содержащее максимально возможное количество ребер. Эту задачу можно преобразовать в задачу о максимальном потоке, построив сеть $N=(X\cup Y\cup \{s,t\},E')$, где

1. $E'$ содержит ребра в $G$ направленный из $X$ к $Y$.
2. $(s,x)\in E'$ для каждого $x\in X$ и $(y,t)\in E'$ для каждого $y\in Y$.
3. $c(e)=1$ для каждого $e\in E'$ (См. рис. 4.3.1).

Тогда значение максимального расхода в $N$ равен размеру максимального паросочетания в $G$, а максимальное соответствие мощности можно найти, взяв те ребра, которые имеют поток $1$ в интегральном макс-потоке.

Минимальное покрытие пути в ориентированном ациклическом графе

Дан ориентированный ациклический граф $G=(V,E)$, нам нужно найти минимальное количество непересекающихся путей, покрывающих каждую вершину в $V$. Мы можем построить двудольный граф $G'=(V_{\textrm {out}}\cup V_{\textrm {in}},E')$ от $G$, где

1. $V_{\textrm {out}}=\{v_{\textrm {out}}\mid v\in V\land v{\text{ has outgoing edge(s)}}\}$
2. $V_{\textrm {in}}=\{v_{\textrm {in}}\mid v\in V\land v{\text{ has incoming edge(s)}}\}$
3. $E'=\{(u_{\textrm {out}},v_{\textrm {in}})\in V_{out}\times V_{in}\mid (u,v)\in E\}$.

Тогда можно показать, что $G'$ имеет соответствие $M$ размера $m$ тогда и только тогда, когда $G$ имеет покрытие пути, не пересекающееся по вершинам $C$ содержащий $m$ края и $n-m$ пути, где $n$ это количество вершин в $G$. Следовательно, задачу можно решить, найдя паросочетание максимальной мощности в $G'$ вместо.

Предположим, мы нашли соответствие $M$ из $G'$, и построил покрытие $C$ от этого. Интуитивно, если две вершины $u_{\mathrm {out} },v_{\mathrm {in} }$ сопоставляются в $M$, то край $(u,v)$ содержится в $C$. Очевидно, что число ребер в $C$ является $m$. Чтобы увидеть это $C$ является вершинно-непересекающимся, учтите следующее:

1. Каждая вершина $v_{\textrm {out}}$ в $G'$ может быть несовпадающим в $M$, и в этом случае не остается ребер, выходящих $v$ в $C$; или его можно совместить , и в этом случае останется ровно одно ребро $v$ в $C$. В любом случае из любой вершины выходит не более одного ребра. $v$ в $C$.
2. Аналогично для каждой вершины $v_{\textrm {in}}$ в $G'$ – если оно совпадает, в $v$ в $C$; в противном случае $v$ не имеет входящих ребер в $C$.

Таким образом, ни одна вершина не имеет двух входящих или двух исходящих ребер. $C$, что означает все пути в $C$ вершинно непересекающиеся.

Чтобы показать, что обложка $C$ имеет размер $n-m$, мы начинаем с пустой оболочки и постепенно строим ее. Чтобы добавить вершину $u$ к обложке, мы можем либо добавить его к существующему пути, либо создать новый путь нулевой длины, начинающийся с этой вершины. Первый случай применим всякий раз, когда либо $(u,v)\in E$ и некоторый путь в обложке начинается с $v$, или $(v,u)\in E$ и некоторый путь заканчивается в $v$. Последний случай всегда применим. В первом случае общее количество ребер в покрытии увеличивается на 1, а количество путей остается прежним; в последнем случае количество путей увеличивается, а количество ребер остается прежним. Теперь ясно, что, охватив все $n$ вершин, сумма числа путей и ребер в покрытии равна $n$. Следовательно, если число ребер в покрытии равно $m$, количество путей $n-m$.

Максимальный поток с вершинными мощностями

Рис. 4.4.1. Преобразование задачи о максимальном потоке с ограничением пропускной способности вершин в исходную задачу о максимальном потоке путем разделения узлов

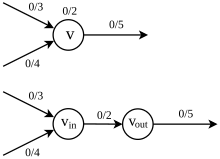
Позволять $N=(V,E)$ быть сетью. Предположим, что в каждом узле есть пропускная способность в дополнение к пропускной способности ребра, то есть отображение $c:V\to \mathbb {R} ^{+},$ такой, что поток $f$ должно удовлетворять не только ограничению пропускной способности и сохранению потоков, но и ограничению пропускной способности вершины.

$\sum _{i\in V}f_{iv}\leq c(v)\qquad \forall v\in V\backslash \{s,t\}.$

Другими словами, количество потока, проходящего через вершину, не может превышать ее пропускную способность. Чтобы найти максимальный поток через $N$, мы можем преобразовать задачу в задачу о максимальном потоке в исходном смысле, разложив $N$. Во-первых, каждый $v\in V$ заменяется на $v_{\text{in}}$ и $v_{\text{out}}$, где $v_{\text{in}}$ соединен ребрами, входящими в $v$ и $v_{\text{out}}$ соединен с ребрами, выходящими из $v$, затем назначьте емкость $c(v)$ до края, соединяющего $v_{\text{in}}$ и $v_{\text{out}}$ (см. рис. 4.4.1). В этой расширенной сети ограничение пропускной способности вершин удалено, и поэтому проблему можно рассматривать как исходную задачу о максимальном потоке.

Максимальное количество путей от s до t

Учитывая ориентированный граф $G=(V,E)$ и две вершины $s$ и $t$, нам нужно найти максимальное количество путей из $s$ к $t$. Эта проблема имеет несколько вариантов:

1. Пути должны быть непересекающимися по ребрам. Эту задачу можно преобразовать в задачу о максимальном потоке, построив сеть $N=(V,E)$ от $G$, с $s$ и $t$ являясь источником и стоком $N$ соответственно, и присваивая каждому ребру пропускную способность $1$. В этой сети максимальный поток равен $k$ если есть $k$ пути, не пересекающиеся по ребрам.

2. Пути должны быть независимыми, т.е. непересекающимися по вершинам (за исключением $s$ и $t$). Мы можем построить сеть $N=(V,E)$ от $G$ с емкостями вершин, где емкости всех вершин и всех ребер равны $1$. Тогда значение максимального потока равно максимальному числу независимых путей из $s$ к $t$.

3. Помимо того, что пути не пересекаются по ребрам и/или вершинам, пути также имеют ограничение на длину: мы учитываем только пути, длина которых точно равна $k$, или самое большее $k$. Большинство вариантов этой задачи NP-полны, за исключением малых значений $k$.

Проблема закрытия

Основная статья: Проблема закрытия

Замыкание из ориентированного графа — это набор вершин C которого ни одно ребро не выходит C. , из Задача замыкания — это задача поиска замыкания максимального или минимального веса в ориентированном графе, взвешенном по вершинам. Ее можно решить за полиномиальное время, используя редукцию к задаче о максимальном расходе.

Реальные приложения

Выбывание в бейсболе

Построение сетевого потока для задачи исключения бейсбола

В в бейсболе задаче на выбывание n в лиге соревнуются команд. На определенном этапе сезона лиги w _i — количество побед, r _i — количество игр, которые осталось сыграть команде i, а r _ij — количество игр, оставшихся против команды j . Команда выбывает, если у нее нет шансов завершить сезон на первом месте. Задача задачи на выбывание в бейсболе состоит в том, чтобы определить, какие команды выбывают в каждый момент сезона. Шварц предложил метод, который сводит эту проблему к максимальному сетевому потоку. В этом методе создается сеть, чтобы определить, ли команда k выбывает .

Пусть G = ( V , E ) — сеть, в которой s , t ∈ V являются источником и стоком соответственно. Добавляется игровой узел _ij , который представляет количество игр между этими двумя командами. Мы также добавляем командный узел для каждой команды и соединяем каждый игровой узел { i , j } с i < j с V и соединяем каждый из них из s ребром с емкостью r _ij – которая представляет количество игр между этими двумя команды. Мы также добавляем по одному командному узлу для каждой команды и соединяем каждый игровой узел { i , j } с двумя командными узлами i и j , чтобы гарантировать победу одного из них. На этих ребрах нет необходимости ограничивать величину потока. , ребра создаются от узла команды i до узла-приемника t и емкость wk _rk + rk _{Наконец} – wi _i устанавливается так, чтобы команда выиграла больше, wk _чем + не _. , Пусть S — множество всех команд, участвующих в лиге, и пусть

$r(S-\{k\})=\sum _{i,j\in \{S-\{k\}\} \atop i<j}r_{ij}$.

В этом методе утверждается, что команда k не исключается тогда и только тогда, когда значение потока размера r ( S − { k }) существует в сети G . В упомянутой статье доказано, что данное значение расхода является максимальным значением расхода от s до t .

Расписание авиакомпаний

В авиационной отрасли основной проблемой является составление расписания летных экипажей. Задачу планирования полетов можно рассматривать как применение расширенного максимального сетевого потока. Входными данными этой задачи является набор рейсов F , который содержит информацию о том, куда и когда каждый рейс отправляется и прибывает. В одной из версий планирования полетов цель состоит в том, чтобы составить реальное расписание с участием не более k экипажей.

Для решения этой проблемы используется вариант задачи циркуляции, называемый ограниченной циркуляцией, который является обобщением задач сетевых потоков с добавленным ограничением нижней границы реберных потоков.

Пусть G = ( V , E ) — сеть с s , t ∈ V в качестве узлов источника и приемника. Для источника и пункта назначения каждого рейса i добавляются два узла к V : узел s _i в качестве источника и узел d _i в качестве узла назначения рейса i . также добавляются следующие ребра К E :

1. Ребро с емкостью [0, 1] между s и каждым s _i .
2. Ребро с емкостью [0, 1] между каждым d _i и t .
3. Ребро с емкостью [1, 1] между каждой парой s _i и d _i .
4. Ребро с пропускной способностью [0, 1] между каждым d _i и s _j , если источник s _j достижим за разумное время и стоимость из пункта назначения полета i .
5. Ребро с пропускной способностью [0, ∞ ] между s и t .

В упомянутом методе утверждается и доказывается, что нахождение значения потока k в G между s и t равно нахождению допустимого расписания для набора полетов F с не более чем k экипажами.

Другой вариант составления расписания авиакомпаний — найти минимально необходимое количество экипажей для выполнения всех рейсов. Чтобы найти ответ на эту проблему, создается двудольный граф G' = ( A ∪ B , E ) где каждый рейс имеет копию в наборе A и наборе B. , Если тот же самолет может выполнить рейс после полета i , i ∈ A соединяется с j ∈ B. j Сопоставление в G' порождает расписание для F , и, очевидно, максимальное двустороннее сопоставление в этом графе дает расписание авиакомпании с минимальным количеством экипажей. Как упоминалось в разделе «Приложения» этой статьи, двустороннее сопоставление максимальной мощности является применением задачи максимального потока.

Проблема обращения и спроса

Есть несколько фабрик, производящих товары, и несколько деревень, куда товары нужно доставлять. Они соединены сетью дорог, каждая из которых имеет пропускную способность c для максимального количества товаров, которые могут пройти по ней. Проблема состоит в том, чтобы выяснить, существует ли тираж, удовлетворяющий спрос. Эту задачу можно преобразовать в задачу о максимальном потоке.

1. Добавьте исходный узел s и добавьте ребра из него к каждому узлу фабрики мощностью _с pi , _где pi — _{производительность} фабрики fi _fi .
2. Добавьте узел-приемник t из всех деревень vi _в t где с пропускной способностью d _i, d i _— уровень спроса в деревне vi _{и добавьте ребра} .

Пусть G = ( V , E ) будет этой новой сетью. Существует обращение, удовлетворяющее спрос тогда и только тогда, когда:

Максимальное значение расхода ( G ) $=\sum _{i\in v}d_{i}$.

Если существует циркуляция, рассмотрение решения о максимальном потоке даст ответ о том, сколько товаров необходимо отправить по конкретной дороге для удовлетворения спроса.

Задачу можно расширить, добавив нижнюю оценку потока на некоторых ребрах.

Сегментация изображений

Исходное изображение размером 8х8.

Сеть построена из растрового изображения. Исток слева, сток справа. Чем темнее край, тем больше его емкость. a _i имеет высокий уровень, когда пиксель зеленый, b _i, когда пиксель не зеленый. Все штрафы _pij одинаковы.

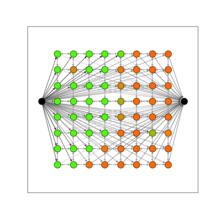
В своей книге Кляйнберг и Тардос представляют алгоритм сегментации изображения. Они представляют алгоритм поиска фона и переднего плана в изображении. Точнее, алгоритм принимает растровое изображение в качестве входных данных, моделируемых следующим образом: a _i ≥ 0 — это вероятность того, что пиксель i принадлежит переднему плану, b _i ≥ 0 — вероятность того, что пиксель i принадлежит фону, а p _ij — это штраф, если два соседних пикселя i и j располагаются один на переднем плане, а другой на заднем. Цель состоит в том, чтобы найти раздел ( A , B ) набора пикселей, который максимизирует следующее количество

$q(A,B)=\sum _{i\in A}a_{i}+\sum _{i\in B}b_{i}-\sum _{\begin{matrix}i,j{\text{ adjacent}}\\|A\cap \{i,j\}|=1\end{matrix}}p_{ij}$,

Действительно, для пикселей в A (считающихся передним планом) мы получаем a _i ; для всех пикселей в B (считающихся фоном) мы получаем b _i . На границе между двумя соседними пикселями i и j мы теряем p _ij . Это эквивалентно минимизации количества

$q'(A,B)=\sum _{i\in A}b_{i}+\sum _{i\in B}a_{i}+\sum _{\begin{matrix}i,j{\text{ adjacent}}\\|A\cap \{i,j\}|=1\end{matrix}}p_{ij}$

потому что

$q(A,B)=\sum _{i\in A\cup B}a_{i}+\sum _{i\in A\cup B}b_{i}-q'(A,B).$

Минимальный разрез, отображаемый в сети (треугольники VS круги).

Теперь мы создадим сеть, узлами которой являются пиксель, а также источник и приемник, см. рисунок справа. Мы соединяем источник с пикселем i ребром веса a _i . Мы соединяем пиксель i со стоком ребром веса b _i . Мы соединяем пиксель i пикселем j с весом pij _с . Теперь осталось вычислить минимальный разрез в этой сети (или, что то же самое, максимальный поток). На последнем рисунке показан минимальный разрез.

Расширения

1. В потоке с минимальной стоимостью каждое ребро ( u ,v) имеет коэффициент стоимости auv _{задаче о} помимо пропускной способности . Если поток через ребро равен f _uv , то общая стоимость равна a _uv f _uv . Требуется найти поток заданной величины d с наименьшей стоимостью. В большинстве вариантов коэффициенты затрат могут быть как положительными, так и отрицательными. Для решения этой задачи существуют различные алгоритмы с полиномиальным временем.

2. Проблема максимального потока может быть дополнена дизъюнктивными ограничениями : отрицательное дизъюнктивное ограничение говорит, что определенная пара ребер не может одновременно иметь ненулевой поток; положительные дизъюнктивные ограничения говорят, что в некоторой паре ребер хотя бы одно должно иметь ненулевой поток. При отрицательных ограничениях проблема становится сильно NP-трудной даже для простых сетей. При положительных ограничениях задача является полиномиальной, если разрешены дробные потоки, но может быть сильно NP-трудной, если потоки должны быть целыми.

Дальнейшее чтение

• Джозеф Чериян и Курт Мельхорн (1999). «Анализ правила выбора самого высокого уровня в алгоритме preflow-push max-flow». Письма об обработке информации . 69 (5): 239–242. CiteSeerX   10.1.1.42.8563 . дои : 10.1016/S0020-0190(99)00019-8 .
• Дэниел Д. Слитор и Роберт Э. Тарджан (1983). «Структура данных для динамических деревьев» (PDF) . Журнал компьютерных и системных наук . 26 (3): 362–391. дои : 10.1016/0022-0000(83)90006-5 . ISSN   0022-0000 .
• Юджин Лоулер (2001). «4. Сетевые потоки». Комбинаторная оптимизация: сети и матроиды . Дувр. стр. 109–177. ISBN  978-0-486-41453-9 .