Гильотинная резка

Безгильотинный разрез: эти прямоугольники *нельзя* разделить, сделав одиночные разрезы пополам поперек плоскости.

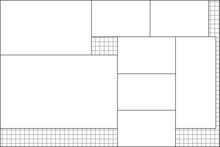
Гильотинная резка — это процесс изготовления небольших прямоугольных изделий фиксированных размеров из заданного большого прямоугольного листа с использованием только гильотинной резки. ( Разрез гильотины также называемый разрезом от края до края ) — это прямая делящая линия, идущая от одного края существующего прямоугольника к противоположному краю, аналогично гильотине для бумаги .

Гильотинная резка особенно распространена в стекольной промышленности. Листы стекла разрезаются по горизонтальным и вертикальным линиям, а затем ломаются по этим линиям, чтобы получить панели меньшего размера. ^[1] Он также полезен для резки стальных пластин, резки деревянных листов для изготовления мебели и резки картона на коробки. ^[2]

Существуют различные проблемы оптимизации, связанные с гильотинной резкой, такие как: максимизация общей площади производимых деталей или их общей стоимости; минимизируйте количество отходов (неиспользованных частей) большого листа или общее количество листов. Они изучались в области комбинаторной геометрии , исследования операций и промышленного проектирования . ^[3]

Связанная, но другая проблема – это гильотинная перегородка . В этой задаче размеры маленьких прямоугольников не фиксированы заранее. Проблема заключается в том, что исходный лист может быть не прямоугольным, а любым прямолинейным многоугольником. В частности, он может содержать отверстия (представляющие дефекты сырья). Целью оптимизации обычно является минимизация количества маленьких прямоугольников или минимизация общей длины разрезов.

Терминология и предположения

В литературе по гильотинной резке часто используются следующие термины и обозначения.

Большой прямоугольник , также называемый листом заготовки , представляет собой необработанный прямоугольный лист, который следует разрезать. Он характеризуется шириной W ₀ и высотой H ₀ , которые являются основными входными данными для задачи.
Маленькие прямоугольники , также называемые элементами , представляют собой необходимые результаты резки. Они характеризуются шириной w _i и высотой h _i, а для i - 1,..., m , где m - количество прямоугольников. Часто допускается наличие нескольких прямоугольников одинаковых размеров; этом случае пару измерений ( wi _в , hi ₎ часто называют типом .
Шаблон для резки , часто называемый просто шаблоном , представляет собой расположение небольших прямоугольников на листе материала. Его можно задать как последовательность точек ( x _i , y _i ), для i in 1,..., m , где ( x _i , y _i ) — нижняя левая координата прямоугольника i . В таком шаблоне прямоугольник i занимает горизонтальный сегмент ( x _i , x _i + w _i ) и вертикальный сегмент ( y _i , y _i + h _i ).
понимается Под сборкой построение нового прямоугольника путем соединения двух прямоугольников меньшего размера. Из-за ограничения гильотины существует только два типа сборок: в горизонтальной сборке объединенный прямоугольник имеет ширину w _i + w _j и высоту max( h _i , h _j ); в вертикальной сборке объединенный прямоугольник имеет ширину max( w _i ,w _j ) и высоту h _i + h _j . Каждый шаблон можно представить как рекурсивную последовательность сборок. Каждая рекурсивная последовательность сборок соответствует множеству различных шаблонов, имеющих эквивалентную комбинаторную структуру; набор всех шаблонов, соответствующих одной и той же рекурсивной сборке, называется классом гильотинной резки . ^[4]

Некоторые задачи принимают дополнительные входные данные, как описано ниже. Цель состоит в том, чтобы вырезать из необработанного прямоугольника несколько прямоугольников меньшего размера с заданными размерами. Часто делаются следующие предположения: ^[2]

Все разрезы имеют нулевую ширину. если каждый разрез имеет фиксированную ширину d > 0, то проблему можно свести к варианту с нулевой шириной, просто добавив d к wi _{Это не теряет большой общности, поскольку} и h _i для i в 0,... , м .
Целевые размеры нельзя вращать, т. е. w -by- h не относится к тому же типу, что h -by- w . Это не теряет большой общности, поскольку вариант, в котором прямоугольники можно вращать, можно свести к варианту без вращения путем явного добавления повернутых шаблонов.

Проверка заданного шаблона

В задаче проверки шаблона существует шаблон резки, заданный как последовательность точек ( , _yi . ) _{, для} в 1,..., m , где ( xi _, i yi _xi ) — нижний левый угол координата прямоугольника i (есть один прямоугольник каждого целевого измерения). Цель состоит в том, чтобы решить, можно ли реализовать этот шаблон, используя только гильотинные разрезы, и если да, то найти последовательность таких разрезов.

Очевидным необходимым условием является то, что никакие два входных прямоугольника не перекрываются в обоих измерениях. Бен Мессауд, Ченгбин и Эспинауз ^[5] представляют более сильное условие, которое является одновременно необходимым и достаточным. Входные прямоугольники упорядочены слева направо, так что x ₁ ≤ ... ≤ x _m . Существует перестановка p индексов такая, что при этой перестановке прямоугольники будут упорядочены снизу вверх, т. е. y _p₍₁₎ ≤ ... ≤ y _p_{( m )} . Учитывая четыре индекса i ₁ ≤ i ₂ и j ₁ ≤ j ₂ , набор E( i ₁ , i ₂ , j ₁ , j ₂ ) содержит индексы всех прямоугольников, левый нижний угол которых находится в прямоугольнике [ x _i₁ , x _i₂ ] X [ y _p_{( j 1)} , y _p_{( j 2)} ]. Схема резки является гильотинной тогда и только тогда, когда для всех четверок индексов i ₁ ≤ i ₂ и j ₁ ≤ j ₂ выполняется хотя бы одно из следующих условий для E( i ₁ , i ₂ , j ₁ , j ₂ ):

E( i ₁ , i ₂ , j ₁ , j ₂ ) содержит не более одного элемента;
Объединение горизонтальных сегментов ( x _i , x _i + w _i ) по всем i в E ( i ₁ , i ₂ , j ₁ , j ₂ ) состоит как минимум из двух непересекающихся интервалов;
Объединение вертикальных сегментов ( y _i , y _i + h _i ) по всем i в E ( i ₁ , i ₂ , j ₁ , j ₂ ) состоит как минимум из двух непересекающихся интервалов.

Условие 2 подразумевает, что прямоугольники в E( i ₁ , i ₂ , j ₁ , j ₂ ) могут быть разделены вертикальным разрезом (проходящим между двумя непересекающимися горизонтальными интервалами); условие 3 подразумевает, что прямоугольники в E( i ₁ , i ₂ , j ₁ , j ₂ ) можно разделить горизонтальным разрезом. Все условия вместе означают, что если какой-либо набор соседних прямоугольников содержит более одного элемента, то их можно разделить каким-либо гильотинным разрезом.

Это условие можно проверить по следующему алгоритму.

На каждой итерации разделите заданный шаблон, содержащий как минимум два прямоугольника, на два непересекающихся подшаблона, используя гильотинный разрез, и выполните рекурсию по каждому подшаблону.
Остановитесь, когда либо все подшаблоны содержат один прямоугольник (в этом случае ответ «да»), либо когда разрезы гильотиной больше невозможны (в этом случае ответ «нет»).

Поиск гильотинного разреза по заданному шаблону производится следующим образом:

Определите m горизонтальных интервалов и расположите их слева направо; определите m вертикальных интервалов и расположите их снизу вверх. Это занимает время O( m log m ).
Объединить перекрывающиеся горизонтальные интервалы и объединить перекрывающиеся вертикальные интервалы. Это занимает время O( m ).
Если после слияния остаются хотя бы два непересекающихся горизонтальных интервала, то возможен вертикальный гильотинный разрез; если имеется хотя бы два непересекающихся вертикальных интервала, то возможен горизонтальный разрез; в противном случае разрез невозможен.

Шаг упорядочивания выполняется один раз, а шаг слияния — m -1 раз. Следовательно, время работы всего алгоритма составляет O( m ²).

Когда алгоритм возвращает «да», он также производит последовательность гильотинных разрезов; когда он возвращает «нет», он также создает определенные подмножества прямоугольников, которые невозможно разделить гильотинными разрезами.

Необходимое и достаточное условие можно использовать для представления задачи резки гильотиной полосы в виде смешанной целочисленной линейной программы . ^[5]^{: сек.5} Их модель имеет 3 n ⁴/4 двоичных переменных и 2 n ⁴ ограничений и считается практически бесполезным.

Поиск оптимальной схемы раскроя

Это варианты задач двумерной резки материала , упаковки в контейнеры и прямоугольной упаковки , где разрезы ограничены гильотинными разрезами. ^[6]

В основной ( невзвешенной ) задаче гильотинной резки требуемый результат представляет собой последовательность гильотинных разрезов, производящих куски заданных размеров, так что общая площадь произведенных кусков максимизируется (эквивалентно, минимизируются отходы от необработанного прямоугольника). .
В взвешенном для каждого целевого измерения i также существует значение vi _. варианте Цель состоит в том, чтобы максимизировать общую стоимость произведенных изделий. если значение каждого целевого измерения будет равно его площади ( vi _{Невзвешенный вариант (минимизация отходов) можно свести к взвешенному варианту ,} = h _i * w _i ).
В варианте с ограничениями для каждого целевого измерения i существует верхняя граница b _i количества изделий этого типа, которые могут быть произведены.
- В варианте с двойными ограничениями для каждого целевого измерения i существует как нижняя граница a _i, так и верхняя граница b _i количества произведенных изделий.
Бинарный вариант — это вариант с ограничениями, в котором каждое целевое измерение должно появляться не более одного раза (т. е. верхняя граница равна 1). Этот случай связан с проблемой принятия решения , цель которой состоит в том, чтобы решить, можно ли изготовить по одному элементу каждого целевого размера с помощью гильотинных разрезов. ^[4]
В задаче о резке полосы гильотиной большой прямоугольник имеет бесконечную высоту (но фиксированную ширину), и цель состоит в том, чтобы разрезать по одному прямоугольнику каждого типа так, чтобы общий используемый материал (эквивалент общей высоты) был минимизирован. Это вариант двумерной задачи упаковки полос .
В задаче минимизации запасов существует бесконечное количество листов одинаковых размеров, и цель состоит в том, чтобы разрезать все необходимые целевые прямоугольники, используя наименьшее возможное количество листов. ^[5] Это вариант двумерной задачи об упаковке контейнеров . ^[7]
k-ступенчатая гильотинная резка — ограниченный вариант гильотинной резки, при котором резка производится не более чем за k этапов: на первом этапе выполняются только горизонтальные разрезы; на втором этапе делаются только вертикальные разрезы; и так далее.
- В двухэтапном варианте дальнейшее различие заключается в том, разрезаются ли все полосы, полученные на первом этапе, в одних и тех же местах (так называемая «1-группа»), в двух разных местах (так называемая «2-группа») или, возможно, в разных местах. локации (так называемые «бесплатные»). ^[8]
1-простая гильотинная резка — это ограниченный вариант гильотинной резки, при котором каждый разрез отделяет один прямоугольник.
- 2 -простая гильотинная резка — это 1-простой узор, так что каждая часть сама по себе является 1-простым узором. p -простые схемы резки могут быть определены рекурсивно. ^[9]

Алгоритмы оптимизации

Особый случай, когда существует только один тип (т. е. все целевые прямоугольники идентичны и имеют одинаковую ориентацию), называется задачей гильотинной загрузки поддонов . Тарновский, Терно и Шайтауэр ^[10] представить полиномиальный алгоритм ее решения.

Однако при наличии двух или более типов все задачи оптимизации, связанные с гильотинной резкой, являются NP-сложными . Ввиду его практической важности различные точные алгоритмы и алгоритмы аппроксимации были разработаны .

Гилмор и Гомори ^[11]^[12] представил динамического программирования рекурсию как для поэтапной, так и для поэтапной гильотинной резки. Однако позже было показано ^[13]^[2] что оба алгоритма содержат ошибки. Бизли ^[2] представил правильный алгоритм динамического программирования.
Сердце ^[13] и Христофидес и Уитлок ^[14] представил процедуры поиска деревьев для бесступенчатой гильотинной резки.
Масден ^[15] и Ван ^[16] представлены эвристические алгоритмы .
Хиффи, М'Халла и Саади ^[6] предложить алгоритм решения задачи гильотины с двойными ограничениями. Это восходящий алгоритм ветвей и границ, использующий поиск по принципу «наилучшее первое» .
Клаутио, Жугле и Мукрим ^[4] предложить точный алгоритм решения задачи. Их алгоритм использует компактное представление классов шаблонов гильотинной резки с использованием ориентированного графа , который они называют гильотинным графом . Каждая дуга на этом графике окрашена в один из двух цветов: «горизонтальный» или «вертикальный». Каждый монохроматический направленный цикл в этом графе соответствует сборке. Многократно сокращая монохроматические циклы, можно восстановить рекурсивную последовательность построения, которая представляет класс шаблона резки. Каждый граф-гильотина содержит от m до 2 m -2 дуг. Особый вид гильотинных графов, называемый нормальными гильотинными графами, обладает интересным свойством содержать уникальную гамильтонову схему . Сортировка вершин в соответствии с этой схемой делает граф хорошо отсортированным нормальным гильотинным графом ; между такими графами и классами разрезов существует взаимно однозначное соответствие. Затем они решают задачу оптимизации, используя программирование в ограничениях на пространстве хорошо отсортированных нормальных гильотинных графов.
Руссо, Бочча, Сфорца и Стерле ^[8] просмотрите более 90 статей, посвященных бесступенчатой ограниченной гильотинной резке (с верхними границами количества), как взвешенной, так и невзвешенной. Существует два основных подхода к точным решениям: динамическое программирование и поиск по дереву (ветви и границы). Подходы к поиску по дереву далее подразделяются на восходящие (начиная с отдельных прямоугольников и используя построения для построения всего листа) или сверху вниз . Во всех подходах важно найти хорошие нижние и верхние границы, чтобы эффективно обрезать пространство поиска. Эти границы часто возникают в результате решений связанных вариантов, например неограниченных, поэтапных и негильотинных вариантов.
Абу Мсабах, Слиман и Ахмед Риад Баба-Али. «Новая эвристика размещения гильотины в сочетании с улучшенным генетическим алгоритмом для решения проблемы ортогональной резки». Международная конференция IEEE 2011 по промышленной инженерии и инженерному менеджменту . ИИЭР, 2011.
Абу-Мсабах, Слиман, Ахмед-Риад Баба-Али и Басма Сагер. «Генетический алгоритм контролируемой стабильности с новой эвристикой размещения гильотины BLF2G для решения проблемы ортогонального режущего материала». Международный журнал когнитивной информатики и естественного интеллекта (IJCINI) 13, вып. 4 (2019): 91-111.

Реализации

Макхейл и Шах ^[17] написал программу на Прологе, реализующую алгоритм в любое время : он генерирует приблизительно оптимальные решения за заданный промежуток времени, а затем улучшает их, если пользователь дает больше времени. Программа использовалась производителем специальной бумаги и позволила сократить время, необходимое для верстки листов, и одновременно сократить количество отходов.

Гильотина разделения

Разделение гильотиной — это родственная задача, в которой входными данными является набор n попарно непересекающихся выпуклых объектов на плоскости, и цель состоит в том, чтобы разделить их с помощью последовательности гильотинных разрезов. Очевидно, что невозможно разделить их все. Хорхе Уррутия Галисия спросила ^[18] можно ли выделить из них постоянную часть, то есть существует ли константа c такая, что в любом таком наборе размера n существует подмножество размера cn, которое можно отделить гильотиной.

Пах и Тардос ^[19] доказал:

Если все объекты имеют одинаковый размер, то можно разделить их постоянную долю. Формально, если все объекты содержат круг радиуса r и содержатся в круге радиуса R , то существует сепарабельное множество размера ${\frac {\pi r^{2}}{128R^{2}}}n\approx {\frac {1}{40.7(R/r)^{2}}}n$ . Доказательство : постройте сетку с размером ячеек 8 R на 8 R. Перемещайте сетку равномерно и случайным образом. Каждый объект пересекается горизонтальной линией с вероятностью 1/4 и вертикальной линией с вероятностью 1/4, поэтому ожидаемое количество пересекающихся объектов равно $n/2$ . Следовательно, существуют линии сетки, пересекающиеся не более чем $n/2$ объекты. Поскольку площадь каждой ячейки сетки равна $(8R)^{2}$ и площадь каждого объекта не менее $\pi r^{2}$ , каждая ячейка содержит не более ${\frac {(8R)^{2}}{\pi r^{2}}}$ объекты. Выберите по одному объекту из каждой ячейки и отделите его от других объектов в той же ячейке. Общее число объектов, разделенных таким образом, не менее ${\frac {n}{2}}/{\frac {(8R)^{2}}{\pi r^{2}}}={\frac {\pi r^{2}}{128R^{2}}}n.$ Аналогичный аргумент для случая единичных квадратов дает ${\frac {1}{27}}n.$
Если объекты представляют собой отрезки прямых, то в некоторых случаях только не более $O(n^{\log _{3}{2}})\approx O(n^{0.63})$ из них можно разделить. В частности, для каждого натурального числа k существует семейство $3^{k}$ непересекающиеся интервалы такие, что не более $2^{k}$ из них можно разделить.
В любом наборе из n выпуклых объектов не менее $\Omega (n^{1/3})$ можно разделить.
В любом наборе из n отрезков прямых не менее $\Omega (n^{1/2})$ можно разделить. Они предполагают, что наихудший случай может быть достигнут с помощью отрезков прямых.
В любом наборе из n прямоугольников, параллельных осям, не менее $n/(2\log {n})$ можно разделить. Они предполагают, что $\Omega (n)$ можно разделить; эта гипотеза все еще остается открытой.
В любой коллекции R - толстых объектов (наименьший содержащий диск не более чем в R раз превышает самый большой содержащийся диск), по крайней мере $n/(c_{R}\log {n})$ $n/(c_{R}\log {n})$ объекты могут быть сохранены, где $c_{R}$ $c_{R}$ — константа, зависящая только R. от
- Аналогичная теорема справедлива и в более высоких измерениях: число разделимых объектов равно $n/c(R,d)(\log {n})^{d}$ .
Все эти отделимые подсемейства могут быть построены во времени. $O(n\log {n})$ . Если объекты представляют собой многоугольники с N сторонами, то разделительные линии можно вычислить за время. $O(N+n\log {n})$ .

Абед, Чалермсук, Корреа, Карренбауэр, Перес-Лантеро, Сото и Визе ^[20] доказал:

В любом наборе из n единичных квадратов, параллельных осям, можно разделить не менее n /2, а есть случаи, когда не более n /2. можно разделить
В любом наборе из n осей-параллельных квадратов не менее n /81. можно выделить
В любом наборе из n осей-параллельных квадратов с весами можно выделить не менее 4/729 от общего веса.
В любом наборе из n параллельных осей d -мерных кубов с весами $1/2^{O(d)}$ от общего веса можно отделить.
Что касается гипотезы о возможности раздельного $\Omega (n)$ прямоугольник, параллельный осям, хотя они и не решают его, они показывают, что, если это правильно, то это подразумевает алгоритм аппроксимации O (1) к задаче о максимальном непересекающемся наборе прямоугольников, параллельных осям во времени. $O(n^{5})$ .

Хан и Питту ^[21] доказал:

С n осями-параллельными прямоугольниками, если только $o(\log \log n)$ этапы разрешены, то разделить их невозможно $\Omega (n)$ прямоугольники.
Когда прямоугольники взвешены, если только $o(\log {n}/\log \log {n})$ этапы разрешены, то разделить их невозможно $\Omega (n)$ веса.
Существует простой двухэтапный алгоритм, который разделяет $n/(1+\log _{2}{n})$ прямоугольники. Алгоритм разбивает прямоугольники на $1+\log _{2}{n}$ подмножества (называемые «уровнями») и выбирает уровень с наибольшим количеством прямоугольников. Каждый уровень можно разделить двумя гильотинными надрезами. ^[21]^{: Thm.14} Улучшенный алгоритм может отделить $n/\log _{3}{(n+2)}$ прямоугольники.
В любой коллекции толстых прямоугольников , $\Omega (n)$ можно разделить.
В любом наборе из n осей-параллельных квадратов не менее n /40. можно выделить
В любом наборе из n осей-параллельных квадратов с весами можно выделить хотя бы долю 1/80 от общего веса.

См. также:

Больше вариантов

Некоторые недавно изученные варианты проблемы включают в себя:

Гильотинная резка в трех измерениях. ^[22]^[23]
Гильотинная резка, когда необработанный прямоугольник может иметь дефекты, но полученные прямоугольники должны быть бездефектными. ^[24]

Ссылки

^ Тлилейн, Лидия; Вио, Квентин (18 мая 2018 г.). «Описание проблемы оптимизации резки Challenge ROADEF / EURO 2018» (PDF) . Вызов ROADEF/EURO . РОАДЭФ . Проверено 13 июня 2019 г.
^ Jump up to: ^а ^б ^с ^д Бизли, Дж. Э. (1 апреля 1985 г.). «Алгоритмы неограниченной двумерной гильотинной резки» . Журнал Общества операционных исследований . 36 (4): 297–306. дои : 10.1057/jors.1985.51 . ISSN 0160-5682 . S2CID 58059319 .
^ Герхард Вешер, Хайке Хауснер, Хольгер Шуман, Улучшенная типология проблем резки и упаковки, European Journal of Operational Research 183 (2007) 1109–1130, [1] Архивировано 20 декабря 2016 г. в Wayback Machine.
^ Jump up to: ^а ^б ^с Клаутио, Франсуа; Жугле, Антуан; Мукрим, Азиз (17 октября 2011 г.). «Новая теоретико-графовая модель для задачи гильотины» . ИНФОМС Журнал по вычислительной технике . 25 (1): 72–86. дои : 10.1287/ijoc.1110.0478 . ISSN 1091-9856 .
^ Jump up to: ^а ^б ^с Бен Мессауд, Саид; Чу, Чэнбинь; Эспинуз, Мари-Лора (16 ноября 2008 г.). «Характеристика и моделирование гильотинных ограничений» . Европейский журнал операционных исследований . 191 (1): 112–126. дои : 10.1016/j.ejor.2007.08.029 . ISSN 0377-2217 .
^ Jump up to: ^а ^б М. Хифи, Р. М'Халла и Т. Саади, Приближенные и точные алгоритмы для двумерной задачи гильотинной резки материала с двойными ограничениями. Вычислительная оптимизация и приложения, том 42, номер 2 (2009), 303–326, два : 10.1007/s10589-007-9081-5
^ Карлье, Жак; Клаутио, Франсуа; Мукрим, Азиз (1 августа 2007 г.). «Новые процедуры приведения и нижние оценки для двумерной задачи упаковки контейнеров с фиксированной ориентацией» . Компьютеры и исследования операций . 34 (8): 2223–2250. дои : 10.1016/j.cor.2005.08.012 . ISSN 0305-0548 .
^ Jump up to: ^а ^б Руссо, Мауро; Бочча, Маурицио; Сфорца, Антонио; Стерле, Клаудио (2020). «Задача двумерной гильотинной резки с ограничениями: обзор верхней границы и категоризация» . Международные сделки в области операционных исследований . 27 (2): 794–834. дои : 10.1111/itor.12687 . ISSN 1475-3995 . S2CID 195551953 .
^ Шайтауэр, Гунтрам (1993). «Расчет оптимальных φ -простых схем гильотинной резки» (PDF) . Журнал обработки информации и кибернетики . 29 (2): 115–128.
^ Тарновски, А.Г.; Терно, Дж.; Шайтауэр, Г. (1 ноября 1994 г.). «Полиномиальный алгоритм решения задачи гильотинной загрузки поддонов» . ИНФОР: Информационные системы и операционные исследования . 32 (4): 275–287. дои : 10.1080/03155986.1994.11732257 . ISSN 0315-5986 .
^ Гилмор, ПК; Гомори, Р.Э. (1 февраля 1965 г.). «Задачи многоэтапного раскроя заготовки двух и более измерений» . Исследование операций . 13 (1): 94–120. дои : 10.1287/опре.13.1.94 . ISSN 0030-364X .
^ Гилмор, ПК; Гомори, Р.Э. (1 декабря 1966 г.). «Теория и вычисление ранцевых функций» . Исследование операций . 14 (6): 1045–1074. дои : 10.1287/опре.14.6.1045 . ISSN 0030-364X .
^ Jump up to: ^а ^б Герц, JC (сентябрь 1972 г.). «Рекурсивная вычислительная процедура для двумерной резки заготовки» . Журнал исследований и разработок IBM . 16 (5): 462–469. дои : 10.1147/rd.165.0462 . ISSN 0018-8646 .
^ Христофидес, Никос; Уитлок, Чарльз (1 февраля 1977 г.). «Алгоритм решения задач двумерного резания» . Исследование операций . 25 (1): 30–44. дои : 10.1287/опре.25.1.30 . ISSN 0030-364X .
^ OBG Масден (1980), рабочий документ IMSOR, Технический университет Дании, Люнгбю
^ Ван, ПЮ (1 июня 1983 г.). «Два алгоритма решения задач двумерной резки заготовки с ограничениями» . Исследование операций . 31 (3): 573–586. дои : 10.1287/опре.31.3.573 . ISSN 0030-364X .
^ Майкл Л. Макхейл, Рошан П. Шах обрезает гильотину до нужного размера. Журнал PC AI, том 13, номер 1, январь/февраль 1999 г. http://www.amzi.com/articles/papercutter.htm
^ Проблема, представленная на ACCOTA '96, Комбинаторные и вычислительные аспекты топологии и алгебры оптимизации, Таско, Мексика, 1996 г.
^ Пах, Дж.; Тардос, Г. (2000). «Резание стекла» . Дискретная и вычислительная геометрия . 24 (2–3): 481–496. дои : 10.1007/s004540010050 . ISSN 0179-5376 . S2CID 1737527 .
^ Абед, Фидаа; Чалермсук, Паринья; КОРРЕА, Хосе; Карренбауэр, Андреас; Перес-Лантеро, Пабло; Сото, Хосе А.; Визе, Андреас (2015). О последовательности гильотинной резки . стр. 1–19. doi : 10.4230/LIPIcs.APPROX-RANDOM.2015.1 . ISBN 978-3-939897-89-7 .
^ Jump up to: ^а ^б Хан, Ариндам; Питту, Мадхусудхан Редди (2020). Бырка, Ярош\лоу; Мека, Рагху (ред.). «О гильотинной разделимости квадратов и прямоугольников» . Аппроксимация, рандомизация и комбинаторная оптимизация. Алгоритмы и методы (ПРИБЛИЗИТЕЛЬНО/СЛУЧАЙНО 2020) . Международные труды Лейбница по информатике (LIPIcs). 176 . Дагштуль, Германия: Schloss Dagstuhl – Leibniz-Zentrum für Informatik: 47:1–47:22. doi : 10.4230/LIPIcs.APPROX/RANDOM.2020.47 . ISBN 978-3-95977-164-1 .
^ МАРТИН, Мэтью; Оливейра, Хосе Фернандо; СИЛЬВА, Эльза; МОРАБИТО, Рейнальдо; Мунари, Педро (08.11.2020). «Задачи трехмерной гильотинной резки с ограниченными шаблонами: формулировки MILP и восходящий алгоритм» . Экспертные системы с приложениями . 168 : 114257. doi : 10.1016/j.eswa.2020.114257 . ISSN 0957-4174 . S2CID 228839108 .
^ Баазауи, М.; Ханафи, С.; Камун, Х. (1 ноября 2014 г.). «Математическая формулировка и нижняя оценка трехмерной задачи упаковки контейнеров с несколькими размерами (MBSBPP): пример тунисской промышленности» . 2014 Международная конференция по управлению, принятию решений и информационным технологиям (CoDIT) . стр. 219–224. дои : 10.1109/CoDIT.2014.6996896 . ISBN 978-1-4799-6773-5 . S2CID 18598442 .
^ Мартин, Матеус; Хокама, Педро HDB; Морабито, Рейнальдо; Мунари, Педро (02 мая 2020 г.). «Двумерная задача гильотинной резки с ограничениями с дефектами: формулировка ILP, разложение Бендерса и алгоритм на основе CP» . Международный журнал производственных исследований . 58 (9): 2712–2729. дои : 10.1080/00207543.2019.1630773 . ISSN 0020-7543 . S2CID 197434029 .

Абу Мсабах, Слиман и Ахмед Риад Баба-Али. «Новая эвристика размещения гильотины в сочетании с улучшенным генетическим алгоритмом для решения проблемы ортогональной резки». Международная конференция IEEE 2011 по промышленной инженерии и инженерному менеджменту . ИИЭР, 2011.

[1] Тлилейн, Лидия; Вио, Квентин (18 мая 2018 г.). «Описание проблемы оптимизации резки Challenge ROADEF / EURO 2018» (PDF) . Вызов ROADEF/EURO . РОАДЭФ . Проверено 13 июня 2019 г.

[:0-2] Jump up to: ^а ^б ^с ^д Бизли, Дж. Э. (1 апреля 1985 г.). «Алгоритмы неограниченной двумерной гильотинной резки» . Журнал Общества операционных исследований . 36 (4): 297–306. дои : 10.1057/jors.1985.51 . ISSN 0160-5682 . S2CID 58059319 .

[3] Герхард Вешер, Хайке Хауснер, Хольгер Шуман, Улучшенная типология проблем резки и упаковки, European Journal of Operational Research 183 (2007) 1109–1130, [1] Архивировано 20 декабря 2016 г. в Wayback Machine.

[:3-4] Jump up to: ^а ^б ^с Клаутио, Франсуа; Жугле, Антуан; Мукрим, Азиз (17 октября 2011 г.). «Новая теоретико-графовая модель для задачи гильотины» . ИНФОМС Журнал по вычислительной технике . 25 (1): 72–86. дои : 10.1287/ijoc.1110.0478 . ISSN 1091-9856 .

[:4-5] Jump up to: ^а ^б ^с Бен Мессауд, Саид; Чу, Чэнбинь; Эспинуз, Мари-Лора (16 ноября 2008 г.). «Характеристика и моделирование гильотинных ограничений» . Европейский журнал операционных исследований . 191 (1): 112–126. дои : 10.1016/j.ejor.2007.08.029 . ISSN 0377-2217 .

[:2-6] Jump up to: ^а ^б М. Хифи, Р. М'Халла и Т. Саади, Приближенные и точные алгоритмы для двумерной задачи гильотинной резки материала с двойными ограничениями. Вычислительная оптимизация и приложения, том 42, номер 2 (2009), 303–326, два : 10.1007/s10589-007-9081-5

[7] Карлье, Жак; Клаутио, Франсуа; Мукрим, Азиз (1 августа 2007 г.). «Новые процедуры приведения и нижние оценки для двумерной задачи упаковки контейнеров с фиксированной ориентацией» . Компьютеры и исследования операций . 34 (8): 2223–2250. дои : 10.1016/j.cor.2005.08.012 . ISSN 0305-0548 .

[:5-8] Jump up to: ^а ^б Руссо, Мауро; Бочча, Маурицио; Сфорца, Антонио; Стерле, Клаудио (2020). «Задача двумерной гильотинной резки с ограничениями: обзор верхней границы и категоризация» . Международные сделки в области операционных исследований . 27 (2): 794–834. дои : 10.1111/itor.12687 . ISSN 1475-3995 . S2CID 195551953 .

[9] Шайтауэр, Гунтрам (1993). «Расчет оптимальных φ -простых схем гильотинной резки» (PDF) . Журнал обработки информации и кибернетики . 29 (2): 115–128.

[10] Тарновски, А.Г.; Терно, Дж.; Шайтауэр, Г. (1 ноября 1994 г.). «Полиномиальный алгоритм решения задачи гильотинной загрузки поддонов» . ИНФОР: Информационные системы и операционные исследования . 32 (4): 275–287. дои : 10.1080/03155986.1994.11732257 . ISSN 0315-5986 .

[11] Гилмор, ПК; Гомори, Р.Э. (1 февраля 1965 г.). «Задачи многоэтапного раскроя заготовки двух и более измерений» . Исследование операций . 13 (1): 94–120. дои : 10.1287/опре.13.1.94 . ISSN 0030-364X .

[12] Гилмор, ПК; Гомори, Р.Э. (1 декабря 1966 г.). «Теория и вычисление ранцевых функций» . Исследование операций . 14 (6): 1045–1074. дои : 10.1287/опре.14.6.1045 . ISSN 0030-364X .

[:1-13] Jump up to: ^а ^б Герц, JC (сентябрь 1972 г.). «Рекурсивная вычислительная процедура для двумерной резки заготовки» . Журнал исследований и разработок IBM . 16 (5): 462–469. дои : 10.1147/rd.165.0462 . ISSN 0018-8646 .

[14] Христофидес, Никос; Уитлок, Чарльз (1 февраля 1977 г.). «Алгоритм решения задач двумерного резания» . Исследование операций . 25 (1): 30–44. дои : 10.1287/опре.25.1.30 . ISSN 0030-364X .

[15] OBG Масден (1980), рабочий документ IMSOR, Технический университет Дании, Люнгбю

[16] Ван, ПЮ (1 июня 1983 г.). «Два алгоритма решения задач двумерной резки заготовки с ограничениями» . Исследование операций . 31 (3): 573–586. дои : 10.1287/опре.31.3.573 . ISSN 0030-364X .

[17] Майкл Л. Макхейл, Рошан П. Шах обрезает гильотину до нужного размера. Журнал PC AI, том 13, номер 1, январь/февраль 1999 г. http://www.amzi.com/articles/papercutter.htm

[18] Проблема, представленная на ACCOTA '96, Комбинаторные и вычислительные аспекты топологии и алгебры оптимизации, Таско, Мексика, 1996 г.

[19] Пах, Дж.; Тардос, Г. (2000). «Резание стекла» . Дискретная и вычислительная геометрия . 24 (2–3): 481–496. дои : 10.1007/s004540010050 . ISSN 0179-5376 . S2CID 1737527 .

[20] Абед, Фидаа; Чалермсук, Паринья; КОРРЕА, Хосе; Карренбауэр, Андреас; Перес-Лантеро, Пабло; Сото, Хосе А.; Визе, Андреас (2015). О последовательности гильотинной резки . стр. 1–19. doi : 10.4230/LIPIcs.APPROX-RANDOM.2015.1 . ISBN 978-3-939897-89-7 .

[:6-21] Jump up to: ^а ^б Хан, Ариндам; Питту, Мадхусудхан Редди (2020). Бырка, Ярош\лоу; Мека, Рагху (ред.). «О гильотинной разделимости квадратов и прямоугольников» . Аппроксимация, рандомизация и комбинаторная оптимизация. Алгоритмы и методы (ПРИБЛИЗИТЕЛЬНО/СЛУЧАЙНО 2020) . Международные труды Лейбница по информатике (LIPIcs). 176 . Дагштуль, Германия: Schloss Dagstuhl – Leibniz-Zentrum für Informatik: 47:1–47:22. doi : 10.4230/LIPIcs.APPROX/RANDOM.2020.47 . ISBN 978-3-95977-164-1 .

[22] МАРТИН, Мэтью; Оливейра, Хосе Фернандо; СИЛЬВА, Эльза; МОРАБИТО, Рейнальдо; Мунари, Педро (08.11.2020). «Задачи трехмерной гильотинной резки с ограниченными шаблонами: формулировки MILP и восходящий алгоритм» . Экспертные системы с приложениями . 168 : 114257. doi : 10.1016/j.eswa.2020.114257 . ISSN 0957-4174 . S2CID 228839108 .

[23] Баазауи, М.; Ханафи, С.; Камун, Х. (1 ноября 2014 г.). «Математическая формулировка и нижняя оценка трехмерной задачи упаковки контейнеров с несколькими размерами (MBSBPP): пример тунисской промышленности» . 2014 Международная конференция по управлению, принятию решений и информационным технологиям (CoDIT) . стр. 219–224. дои : 10.1109/CoDIT.2014.6996896 . ISBN 978-1-4799-6773-5 . S2CID 18598442 .

[24] Мартин, Матеус; Хокама, Педро HDB; Морабито, Рейнальдо; Мунари, Педро (02 мая 2020 г.). «Двумерная задача гильотинной резки с ограничениями с дефектами: формулировка ILP, разложение Бендерса и алгоритм на основе CP» . Международный журнал производственных исследований . 58 (9): 2712–2729. дои : 10.1080/00207543.2019.1630773 . ISSN 0020-7543 . S2CID 197434029 .

[1]

[2]

[3]

[4]

[5]

[6]

[7]

[8]

[9]

[10]

[11]

[12]

[13]

[14]

[15]

[16]

[17]

[18]

[19]

[20]

[21]

[22]

[23]

[24]