Тета-функции Невилла
В математике тэта-функции Невилла , названные в честь Эрика Гарольда Невилла , [1] определяются следующим образом: [2] [3] [4]
где: K(m) – полный эллиптический интеграл первого рода, , и это эллиптический ном.
Обратите внимание, что функции θ p (z,m) иногда определяются в терминах нома q(m) и пишутся как θ p (z,q) (например, NIST [5] ). Функции также можно записать через τ параметр θ p (z|τ) , где .
Связь с другими функциями
[ редактировать ]Тета-функции Невилла можно выразить через тета-функции Якоби. [5]
где .
Тета-функции Невилла связаны с эллиптическими функциями Якоби . Если pq(u,m) — эллиптическая функция Якоби (p и q — одна из s,c,n,d), то
Примеры
[ редактировать ]Симметрия
[ редактировать ]Сложные 3D-графики
[ редактировать ] | 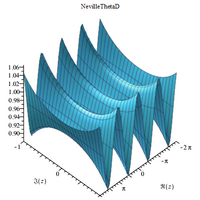 |  | 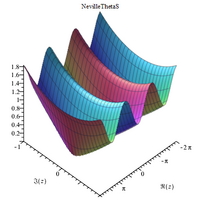 |
Примечания
[ редактировать ]- ^ Абрамовиц и Стегун, стр. 578-579.
- ^ Невилл (1944)
- ^ Сайт математических функций
- ^ Сайт математических функций
- ^ Jump up to: а б Олвер, ФВЮ; и др., ред. (22 декабря 2017 г.). «Цифровая библиотека математических функций NIST (выпуск 1.0.17)» . Национальный институт стандартов и технологий . Проверено 26 февраля 2018 г.
Ссылки
[ редактировать ]- Абрамовиц, Милтон ; Стегун, Ирен Энн , ред. (1983) [июнь 1964 г.]. Справочник по математическим функциям с формулами, графиками и математическими таблицами . Серия «Прикладная математика». Том. 55 (Девятое переиздание с дополнительными исправлениями десятого оригинального издания с исправлениями (декабрь 1972 г.); первое изд.). Вашингтон, округ Колумбия; Нью-Йорк: Министерство торговли США, Национальное бюро стандартов; Дуврские публикации. ISBN 978-0-486-61272-0 . LCCN 64-60036 . МР 0167642 . LCCN 65-12253 .
- Невилл, Э.Х. (Эрик Гарольд) (1944). Эллиптические функции Якоби . Оксфорд Кларендон Пресс.
- Вайсштейн, Эрик В. «Тэта-функции Невилла» . Математический мир .




















