ω-автомат

В теории автоматов , разделе теоретической информатики , ω -автомат (или потоковый автомат ) — это разновидность конечного автомата , который работает на бесконечных, а не на конечных строках в качестве входных данных. Поскольку ω-автоматы не останавливаются, они имеют не просто набор принимающих состояний, а множество условий принятия.

ω-автоматы полезны для определения поведения систем, завершение которых не ожидается, таких как аппаратное обеспечение, операционные системы и системы управления . Для таких систем может потребоваться указать такое свойство, как «для каждого запроса в конечном итоге следует подтверждение» или его отрицание «есть запрос, за которым не следует подтверждение». Первое является свойством бесконечных слов: о конечной последовательности нельзя сказать, что она удовлетворяет этому свойству.

Классы ω-автоматов включают автоматы Бюхи , автоматы Рабина, автоматы Стритта, автоматы четности и автоматы Мюллера , каждый из которых детерминирован или недетерминирован. Эти классы ω-автоматов различаются лишь условием приемки . Все они распознают именно регулярные ω-языки, за исключением детерминированного автомата Бюхи, который строго слабее всех остальных. Хотя все эти типы автоматов распознают один и тот же набор ω-языков , они, тем не менее, различаются краткостью представления для данного ω-языка.

Детерминированные ω-автоматы [ править ]

Формально детерминированный ω-автомат — это набор A = ( Q ,Σ,δ, Q0 _{) ,} , Acc состоящий из следующих компонентов:

Q — конечное множество . Элементы Q называются состояниями A .
Σ — конечное множество алфавитом A. , называемое
δ: Q × Σ → Q — функция, называемая перехода A . функцией
Q ₀ является элементом Q , называемым начальным состоянием.
Acc — условие приемки , формально подмножество Q ^ой.

Входными данными для A является бесконечная строка в алфавите Σ, т. е. это бесконечная последовательность α = ( a ₁ , a ₂ , a ₃ ,...). Прогон определяемую A образом на таком входе представляет собой бесконечную последовательность ρ = ( 2 _, ... ) _{состояний} , r 0 , r 1 , r _{следующим} :

р ₀ знак равно q ₀ .
р ₁ знак равно δ( р ₀ , а ₁ ).
р ₂ знак равно δ( р ₁ , а ₂ ).

...

то есть для каждого i : r _i = δ( r _{i -1} , a _i ).

Основная цель ω-автомата — определить подмножество набора всех входных данных: набор принятых входных данных. В то время как в случае обычного конечного автомата каждый запуск заканчивается состоянием r _n и вход принимается тогда и только тогда, когда r _n является принимающим состоянием, для ω-автоматов определение множества принимаемых входов сложнее. Здесь мы должны рассмотреть весь пробег ρ. Ввод принимается, если соответствующий прогон находится в Acc . Множество принятых входных ω-слов называется распознанным автоматом ω-языком и обозначается L(A).

Определение Acc как подмножества Q ^ойявляется чисто формальным и непригодным для практики, поскольку обычно такие множества бесконечны. Разница между различными типами ω-автоматов (Бюхи, Рабина и др.) состоит в том, как они кодируют те или иные подмножества Acc из Q ^ой как конечные множества и, следовательно, в какие такие подмножества они могут закодировать.

- Недетерминированные ω автоматы

Формально недетерминированный ω-автомат — это набор A = ( Q ,Σ,Δ, Q0 _{) ,} , Acc состоящий из следующих компонентов:

Q — конечное множество . Элементы Q называются состояниями A .
Σ — конечное множество алфавитом A. , называемое
Δ является подмножеством Q Σ × Q и называется отношением перехода A × .
Q ₀ — это подмножество Q , называемое исходным набором состояний.
Acc — условие приемки , подмножество Q ^ой.

В отличие от детерминированного ω-автомата, имеющего функцию перехода δ, недетерминированная версия имеет отношение перехода Δ. Обратите внимание, что Δ можно рассматривать как функцию: Q × Σ → P ( Q ) от Q × Σ до набора степеней P ( Q ). для данного состояния q _n и символа n _{Таким образом ,} следующее состояние q _{n +1} не обязательно определяется однозначно, скорее существует набор возможных следующих состояний.

Серия ,...) состояний , A a на входе α = ( 1 _, a 2 _, a 3 _, ...) — это любая бесконечная последовательность ρ = ( r ₀ , r ₁ , r ₂ которая удовлетворяет следующим условиям :

r ₀ является элементом Q ₀ .
r ₁ является элементом Δ( r ₀ , a ₁ ).
r ₂ является элементом Δ( r ₁ , a ₂ ).

...

то есть для каждого i : r _i является элементом Δ( r _{i -1} , a _i ).

Недетерминированный ω-автомат может допускать множество различных запусков на любом заданном входе или вообще не допускать ни одного. Ввод принимается, если принимается хотя бы один из возможных запусков. Приемлем ли прогон, зависит только от Acc , как и для детерминированных ω-автоматов. Каждый детерминированный ω-автомат можно рассматривать как недетерминированный ω-автомат, взяв Δ в качестве графика δ. В таком случае определения серий и акцептования для детерминированных ω-автоматов являются частными случаями недетерминированных случаев.

Условия приемки [ править ]

Условиями приемки могут быть бесконечные множества ω-слов. Однако люди в основном изучают приемочные условия, которые конечно представимы. Ниже перечислены различные популярные условия принятия.

Прежде чем обсуждать список, давайте сделаем следующее наблюдение. В случае бесконечно работающих систем часто интересно, повторяется ли определенное поведение бесконечно часто. Например, если сетевая карта получает бесконечное количество запросов ping, она может не ответить на некоторые запросы, но должна ответить на бесконечное подмножество полученных запросов ping. Это мотивирует следующее определение: для любого цикла ρ пусть Inf(ρ) — это набор состояний, которые встречаются бесконечно часто в ρ. Представление о том, что определенные состояния посещаются бесконечно часто, будет полезно при определении следующих условий принятия.

Автомат Бюхи — это ω-автомат A , который использует следующее условие приемки для некоторого подмножества F из Q :

Состояние Бючи: A принимает именно те прогоны ρ, для которых Inf(ρ) ∩ F не пусто, т.е. существует принимающее состояние, которое встречается бесконечно часто в ρ.

А Автомат Рабина — это ω-автомат A , который использует следующее условие приемки для некоторого множества Ω пар (B _i ,G _i ) наборов состояний:

Условие Рабина: A принимает ровно те прогоны ρ, для которых существует пара (B _i ,G _i ) в Ω такая, что B _i ∩ Inf(ρ) пусто и G _i ∩ Inf(ρ) не пусто.

Автомат Стритта — это ω-автомат A , который использует следующее условие приемки для некоторого множества Ω пар (B _i ,G _i ) наборов состояний:

Уличное состояние: A принимает именно те прогоны ρ такие, что для всех пар (B _i ,G _i ) в Ω B _i ∩ Inf(ρ) пусто или G _i ∩ Inf(ρ) не пусто.

Автомат четности — это автомат A , набор состояний которого равен Q = {0,1,2,..., k } для некоторого натурального числа k и который имеет следующее условие приемки:

Условие четности: A принимает ρ тогда и только тогда, когда наименьшее число в Inf(ρ) четно.

Автомат Мюллера — это ω-автомат A , который использует следующее условие приемки для подмножества F из P ( Q ) ( множества степеней Q ) :

Условие Мюллера: A принимает именно те серии ρ, для которых Inf(ρ) является элементом F .

Любой автомат Бюхи можно рассматривать как автомат Мюллера. Достаточно заменить F на F ', состоящее из всех подмножеств Q содержащих хотя бы один элемент F. , Точно так же каждый автомат Рабина, Стритта или автомат четности также можно рассматривать как автомат Мюллера.

Пример [ править ]

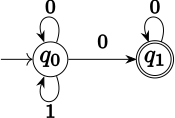
Следующий ω-язык L над алфавитом Σ = {0,1}, который распознается недетерминированным автоматом Бюхи: L состоит из всех ω-слов из Σ ^ойв котором 1 встречается лишь конечное число раз. Недетерминированному автомату Бюхи, распознающему L, нужны только два состояния q ₀ (начальное состояние) и q ₁ . троек ( , _, q0 ) ₎ ( , ₎ q0 q1 _q0,0 ( , _q1,0 q1 ) _q0,1 и ( , _из , q0,0 _{Δ состоит} . F = { q ₁ }. Для любого входа α, в котором 1 встречается только конечное число раз, существует серия, которая остается в состоянии q ₀ до тех пор, пока есть единицы для чтения, а затем переходит в состояние q ₁ . Этот забег успешен. Если единиц бесконечно много, то возможен только один запуск: тот, который всегда остается в состоянии q ₀ . (Как только машина покинула q ₀ и достигла q ₁ , она не может вернуться. Если считывается еще одна 1, состояния-преемника не существует.)

Обратите внимание, что приведенный выше язык не может быть распознан детерминированным автоматом Бюхи , который строго менее выразителен , чем его недетерминированный аналог.

сила ω автоматов Выразительная -

ω-язык над конечным алфавитом Σ — это множество ω-слов над Σ, т. е. это подмножество Σ ^ой. Говорят, что ω-язык над Σ распознается ω-автоматом A (с тем же алфавитом), если он представляет собой множество всех ω-слов, принимаемых A . Выразительная сила класса ω-автоматов измеряется классом всех ω-языков, которые могут быть распознаны некоторым автоматом этого класса.

Недетерминированные автоматы Бюхи, четности, Рабина, Стритта и Мюллера соответственно распознают один и тот же класс ω-языков. ^[1]Они известны как ω-замыкание Клини регулярных языков или как регулярные ω-языки . Используя различные доказательства, можно также показать, что автоматы детерминированной четности, автоматы Рабина, Стритта и Мюллера распознают регулярные ω-языки. Отсюда следует, что класс регулярных ω-языков замкнут относительно дополнения. Однако приведенный выше пример показывает, что класс детерминированных автоматов Бюхи строго слабее.

Преобразование между ω-автоматами [ править ]

Поскольку недетерминированные автоматы Мюллера, Рабина, Стритта, четности и Бюхи одинаково выразительны, их можно переводить друг в друга. Давайте использовать следующую аббревиатуру $\{N,D\}\times \{M,R,S,P,B\}$ : например, NB означает недетерминированный ω-автомат Бюхи, а DP означает детерминированный ω-автомат четности. Тогда имеет место следующее.

Ясно, что любой детерминированный автомат можно рассматривать как недетерминированный.
$NB\rightarrow NR/NS/NP$ без разрушения в пространстве состояний.
$NR\rightarrow NB$ с полиномиальным разрушением в пространстве состояний, т.е. количество состояний в результирующем НБ равно $2nm+1$ , где $n$ количество штатов в составе НБ и $m$ – число акцептирующих пар Рабина (см., например, ^[2]).
$NS/NM/NP\rightarrow NB$ с экспоненциальным разрушением в пространстве состояний.
$NB\rightarrow DR/DP$ с экспоненциальным разрушением в пространстве состояний. Этот результат детерминации использует конструкцию Сафры .

Полный обзор переводов можно найти в указанном веб-источнике. ^[3]

Приложения к разрешимости

ω-автоматы можно использовать для доказательства разрешимости S1S, второго порядка монадической теории натуральных чисел (MSO) под преемником. Автоматы с бесконечным деревом расширяют ω-автоматы до бесконечных деревьев и могут использоваться для доказательства разрешимости S2S , теории MSO с двумя преемниками, и это может быть расширено до теории MSO графов с ограниченной (при фиксированной границе) шириной дерева .

Дальнейшее чтение [ править ]

Фарвер, Берндт (2002), «ω-автоматы», в Гределе, Эрих; Томас, Вольфганг; Уилк, Томас (ред.), Автоматы, логика и бесконечные игры , Конспекты лекций по информатике , Springer, стр. 3–21, ISBN 978-3-540-00388-5 .
Перрен, Доминик; Пин, Жан-Эрик (2004), Бесконечные слова: автоматы, полугруппы, логика и игры , Elsevier , ISBN 978-0-12-532111-2
Томас, Вольфганг (1990), «Автоматы на бесконечных объектах», Ван Леувен, Ян (редактор), Справочник по теоретической информатике, том. B , MIT Press , стр. 133–191, ISBN. 978-0-262-22039-2
Бахадыр Хусаинов; Анил Нероде (6 декабря 2012 г.). Теория автоматов и ее приложения . Springer Science & Business Media. ISBN 978-1-4612-0171-7 .

Ссылки [ править ]

^ Сафра, С. (1988), «О сложности ω-автоматов», Труды 29-го ежегодного симпозиума по основам информатики (FOCS '88) , Вашингтон, округ Колумбия, США: Компьютерное общество IEEE, стр. 319–327. , дои : 10.1109/SFCS.1988.21948 .
^ Эспарса, Хавьер (2017), Теория автоматов: алгоритмический подход (PDF)
^ Бокер, Уди (18 апреля 2018 г.). «Переводы Word-автоматов» . Веб-страница Уди Бокера . Проверено 30 марта 2019 г.

[1] Сафра, С. (1988), «О сложности ω-автоматов», Труды 29-го ежегодного симпозиума по основам информатики (FOCS '88) , Вашингтон, округ Колумбия, США: Компьютерное общество IEEE, стр. 319–327. , дои : 10.1109/SFCS.1988.21948 .

[2] Эспарса, Хавьер (2017), Теория автоматов: алгоритмический подход (PDF)

[3] Бокер, Уди (18 апреля 2018 г.). «Переводы Word-автоматов» . Веб-страница Уди Бокера . Проверено 30 марта 2019 г.

[1]

[2]

[3]