Полигон видимости

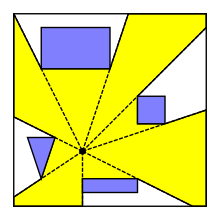
В вычислительной геометрии многоугольник видимости или область видимости для точки $p$ на плоскости среди препятствий — это возможно неограниченная многоугольная область всех точек плоскости, видимых из $p$ . Полигон видимости также можно определить для видимости из сегмента или многоугольника. Многоугольники видимости полезны в робототехнике , видеоиграх и в различных задачах оптимизации, таких как проблема размещения объекта и проблема художественной галереи .

Если многоугольник видимости ограничен, то это многоугольник в форме звезды . Многоугольник видимости ограничен, если все лучи , исходящие из точки, в конечном итоге оканчиваются каким-либо препятствием. Это имеет место, например, если препятствиями являются края простого многоугольника , а $p$ находится внутри многоугольника. В последнем случае полигон видимости можно найти за линейное время . ^[1]^[2]^[3]^[4]

Определения

Формально мы можем определить задачу плоского многоугольника видимости как таковую. Позволять $S$ быть набором препятствий (сегментов или многоугольников) в $\mathbb {R} ^{2}$ . Позволять $p$ быть точкой в $\mathbb {R} ^{2}$ это не находится в пределах препятствия. Тогда многоугольник видимости точки $V$ это набор точек в $\mathbb {R} ^{2}$ , такой, что для каждой точки $q$ в $V$ , сегмент $pq$ не пересекает никаких препятствий $S$ .

Аналогично, многоугольник видимости сегмента или многоугольник видимости края — это часть, видимая для любой точки вдоль сегмента линии .

Приложения

Полигоны видимости полезны в робототехнике . Например, при локализации роботов робот, использующий такие датчики, как лидар, будет обнаруживать препятствия, которые он может видеть, что похоже на многоугольник видимости. ^[5]

Они также полезны в видеоиграх : в многочисленных онлайн-руководствах объясняются простые алгоритмы их реализации. ^[6]^[7]^[8]

Алгоритмы построения полигонов видимости точек

Было предложено множество алгоритмов вычисления многоугольника видимости точки. Для разных вариантов задачи (например, разных типов препятствий) алгоритмы различаются по временной сложности.

Наивные алгоритмы

Наивные алгоритмы легко понять и реализовать, но они не оптимальны , поскольку могут работать намного медленнее, чем другие алгоритмы.

Единый «физический» алгоритм распределения лучей

В реальной жизни светящаяся точка освещает видимую ей область, поскольку излучает свет во всех направлениях. Это можно смоделировать, стреляя лучами во многих направлениях. Предположим, что дело в том, $p$ и множество препятствий $S$ . Тогда псевдокод можно выразить следующим образом:

algorithm naive_bad_algorithm( $p$ ,  $S$ ) is
     $V$  :=  $\emptyset$ 
    for  $\theta =0,\cdots ,2\pi$ :
        // shoot a ray with angle  $\theta$ 
         $r$  :=  $\infty$ 
        for each obstacle in  $S$ :
             $r$  := min( $r$ , distance from  $p$  to the obstacle in this direction)
        add vertex  $(\theta ,r)$  to  $V$ 
    return  $V$

Теперь, если бы можно было перепробовать все бесконечное множество углов, результат был бы правильным. К сожалению, невозможно по-настоящему опробовать каждое направление из-за ограничений компьютеров. Приближение можно создать, отбрасывая множество, скажем, 50 лучей, расположенных на одинаковом расстоянии друг от друга. Однако это не точное решение, поскольку небольшие препятствия могут быть полностью пропущены двумя соседними лучами. Более того, это очень медленно, так как, возможно, придется пропустить много лучей, чтобы получить примерно похожее решение, а выходной многоугольник видимости может иметь гораздо больше вершин, чем необходимо.

Приведение лучей к каждой вершине

Описанный ранее алгоритм можно значительно улучшить как по скорости, так и по правильности, если заметить, что достаточно стрелять лучами только в вершины каждого препятствия. Это связано с тем, что любые изгибы или углы вдоль границы многоугольника видимости должны быть связаны с каким-либо углом (т. е. вершиной) препятствия.

algorithm naive_better_algorithm( $p$ ,  $S$ ) is
     $V$  :=  $\emptyset$ 
    for each obstacle  $b$  in  $S$ :
        for each vertex  $v$  of  $b$ :
            // shoot a ray from  $p$  to  $v$ 
             $r$  := distance from  $p$  to  $v$ 
             $\theta$  := angle of  $v$  with respect to  $p$ 
            for each obstacle  $b'$  in  $S$ :
                 $r$  := min( $r$ , distance from  $p$  to  $b'$ )
            add vertex  $(\theta ,r)$  to  $V$ 
    return  $V$

Приведенный выше алгоритм может быть неверным. Смотрите обсуждение в разделе «Обсуждение».

Временная сложность этого алгоритма составляет $O(n^{2})$ . Это связано с тем, что алгоритм направляет луч в каждый из $n$ вершин, и чтобы проверить, где заканчивается луч, он должен проверить пересечение с каждой из $O(n)$ препятствия. Этого достаточно для многих простых приложений, таких как видеоигры, и поэтому этому методу обучают во многих онлайн-руководствах. ^[8] Однако, как мы увидим позже, существуют более быстрые $O(n\log n)$ алгоритмы (или даже более быстрые, если препятствием является простой многоугольник или имеется фиксированное количество многоугольных отверстий).

Оптимальные алгоритмы для точки простого многоугольника

Учитывая простой многоугольник ${\mathcal {P}}$ и точка $p$ , алгоритм с линейным временем оптимален для вычисления области в ${\mathcal {P}}$ это видно из $p$ . Впервые такой алгоритм был предложен в 1981 году. ^[2] Однако это довольно сложно. В 1983 году был предложен концептуально более простой алгоритм: ^[3] в котором была небольшая ошибка, исправленная в 1987 году. ^[4]

Последний алгоритм будет кратко объяснен здесь. Он просто обходит границу многоугольника. ${\mathcal {P}}$ , обрабатывая вершины в том порядке, в котором они появляются, сохраняя при этом стек вершин ${\mathcal {S}}=s_{0},s_{1},\cdots ,s_{t}$ где $s_{t}$ является вершиной стека. Стек состоит из встреченных до сих пор вершин, видимых $p$ . Если в дальнейшем в ходе выполнения алгоритма встретятся новые вершины, закрывающие часть ${\mathcal {S}}$ , то скрытые вершины в ${\mathcal {S}}$ будет извлечен из стека. К моменту завершения алгоритма ${\mathcal {S}}$ будет состоять из всех видимых вершин, т.е. желаемого полигона видимости. Эффективная реализация была опубликована в 2014 году. ^[9]

Оптимальные алгоритмы для точки в многоугольнике с дырками

Для точки многоугольника с $h$ отверстия и $n$ вершин в сумме, можно показать, что в худшем случае $\Theta (n+h\log h)$ алгоритм оптимален. Такой алгоритм был предложен в 1995 году вместе с доказательством его оптимальности. ^[10] Однако он основан на алгоритме триангуляции многоугольников с линейным временем Шазелла, который чрезвычайно сложен.

Оптимальные алгоритмы для точки среди отрезков

Сегменты, которые пересекаются только в своих конечных точках.

Для точки среди множества $n$ сегментов, которые пересекаются только в своих конечных точках, можно показать, что в худшем случае $\Theta (n\log n)$ алгоритм оптимален. Это связано с тем, что алгоритм многоугольника видимости должен выводить вершины многоугольника видимости в отсортированном порядке, следовательно, задачу сортировки можно свести к вычислению многоугольника видимости. ^[11]

Обратите внимание, что любой алгоритм, вычисляющий многоугольник видимости для точки среди сегментов, можно использовать для вычисления многоугольника видимости для всех других типов многоугольных препятствий, поскольку любой многоугольник можно разложить на сегменты.

Разделяй и властвуй

Алгоритм «разделяй и властвуй» для вычисления многоугольника видимости был предложен в 1987 году. ^[12]

Угловая развертка

Угловая развертка , то есть алгоритм развертки по вращательной плоскости для расчета многоугольника видимости, был предложен в 1985 году. ^[13] и 1986 год. ^[11] Идея состоит в том, чтобы сначала отсортировать все конечные точки сегмента по полярному углу, а затем перебрать их в этом порядке. Во время итерации строка событий сохраняется в виде кучи . Эффективная реализация была опубликована в 2014 году. ^[9]

Обычно пересекающиеся сегменты

Для точки среди обычно пересекающихся сегментов проблема многоугольника видимости сводится за линейное время к задаче о нижней огибающей . Согласно аргументу Давенпорта-Шинцеля , нижняя граница в худшем случае имеет $\Theta (n\alpha (n))$ количество вершин, где $\alpha (n)$ – обратная функция Аккермана . Оптимальный алгоритм «разделяй и властвуй» в худшем случае, работающий в $\Theta (n\log n)$ time был создан Джоном Хершбергером в 1989 году. ^[14]

Ссылки

^ Франко П. Препарата и Майкл Ян Шамос (1985). Вычислительная геометрия. Введение . Спрингер-Верлаг . ISBN 0-387-96131-3 . 1-е издание; 2-е издание, исправленное и дополненное, 1988 г.: ISBN 3-540-96131-3 ; Русский перевод, 1989: ISBN 5-03-001041-6 .
^ Перейти обратно: ^а ^б Эль Джинди, Хосам; Авис, Дэвид (1981). «Линейный алгоритм расчета многоугольника видимости из точки». Журнал алгоритмов . 2 (2): 186–197. дои : 10.1016/0196-6774(81)90019-5 .
^ Перейти обратно: ^а ^б Ли, DT (май 1983 г.). «Видимость простого многоугольника». Компьютерное зрение, графика и обработка изображений . 22 (2): 207–221. дои : 10.1016/0734-189X(83)90065-8 .
^ Перейти обратно: ^а ^б Джо, Барри; Симпсон, РБ (1987). «Исправления алгоритма многоугольника видимости Ли». БИТ Численная математика . 27 (4): 458–473. дои : 10.1007/BF01937271 . S2CID 19112466 .
^ Гибас, Леонидас; Мотвани, Раджив; Рагхаван, Прабхакар (1992). Проблема локализации робота в двух измерениях . Симпозиум ACM-SIAM по дискретным алгоритмам. Общество промышленной и прикладной математики.
^ Лиоу, Никлаус. «SIGHT & LIGHT: как создать 2D-эффекты видимости/теней для вашей игры» . Проверено 9 мая 2014 г.
^ Патель, Амит (5 июля 2012 г.). «Алгоритм 2D видимости» . Проверено 9 мая 2014 г.
^ Перейти обратно: ^а ^б Патель, Амит (5 июля 2012 г.). «Капли в играх: 2D-видимость» . Проверено 9 мая 2014 г.
^ Перейти обратно: ^а ^б Бунгиу, Франциск; Хеммер, Майкл; Хершбергер, Джон; Хуанг, Кан; Креллер, Александр (2014). «Эффективное вычисление полигонов видимости». arXiv : 1403.3905 [ cs.CG ].
^ Хеффернан, Пол; Митчелл, Джозеф (1995). «Оптимальный алгоритм расчета видимости в плоскости» (PDF) . SIAM Journal по вычислительной технике . 24 (1): 184–201. дои : 10.1137/S0097539791221505 . hdl : 1813/8838 .
^ Перейти обратно: ^а ^б Сури, Субхаш; О'Рурк, Джозеф (1986). Оптимальные в худшем случае алгоритмы построения многоугольников видимости с дырками . Симпозиум по вычислительной геометрии. АКМ . стр. 14–23. дои : 10.1145/10515.10517 .
^ Аркин, Э .; Митчелл, Джозеф (1987). Алгоритм оптимальной видимости простого многоугольника со звездообразными отверстиями (Технический отчет). Корнелльский университет по исследованию операций и промышленной инженерии. 746.
^ Асано, Тецуо (1985). Эффективный алгоритм поиска полигона видимости для многоугольной области с дырками . Институт инженеров электроники, информации и связи. Том. 68. стр. 557–559.
^ Хершбергер, Джон (1989). «Нахождение верхнего конверта $n$ сегменты линий в $O(n\log n)$ время». Письма обработки информации . 33 (4): 169–174. doi : 10.1016/0020-0190(89)90136-1 .

Внешние ссылки

http://web.informatik.uni-bonn.de/I/GeomLab/VisPolygon/index.html.en (видимость в простых полигонах - апплетах)

Программное обеспечение

VisiLibity : бесплатная библиотека C++ с открытым исходным кодом для вычислений видимости в плоских полигональных средах.
Visibility-polygon-js : общедоступная библиотека Javascript для вычисления многоугольника видимости точки среди сегментов с использованием метода угловой развертки.

[PS-1] Франко П. Препарата и Майкл Ян Шамос (1985). Вычислительная геометрия. Введение . Спрингер-Верлаг . ISBN 0-387-96131-3 . 1-е издание; 2-е издание, исправленное и дополненное, 1988 г.: ISBN 3-540-96131-3 ; Русский перевод, 1989: ISBN 5-03-001041-6 .

[ea-2] Перейти обратно: ^а ^б Эль Джинди, Хосам; Авис, Дэвид (1981). «Линейный алгоритм расчета многоугольника видимости из точки». Журнал алгоритмов . 2 (2): 186–197. дои : 10.1016/0196-6774(81)90019-5 .

[lee-3] Перейти обратно: ^а ^б Ли, DT (май 1983 г.). «Видимость простого многоугольника». Компьютерное зрение, графика и обработка изображений . 22 (2): 207–221. дои : 10.1016/0734-189X(83)90065-8 .

[js-4] Перейти обратно: ^а ^б Джо, Барри; Симпсон, РБ (1987). «Исправления алгоритма многоугольника видимости Ли». БИТ Численная математика . 27 (4): 458–473. дои : 10.1007/BF01937271 . S2CID 19112466 .

[guibas-5] Гибас, Леонидас; Мотвани, Раджив; Рагхаван, Прабхакар (1992). Проблема локализации робота в двух измерениях . Симпозиум ACM-SIAM по дискретным алгоритмам. Общество промышленной и прикладной математики.

[ncase-6] Лиоу, Никлаус. «SIGHT & LIGHT: как создать 2D-эффекты видимости/теней для вашей игры» . Проверено 9 мая 2014 г.

[redblob-7] Патель, Амит (5 июля 2012 г.). «Алгоритм 2D видимости» . Проверено 9 мая 2014 г.

[redblob2-8] Перейти обратно: ^а ^б Патель, Амит (5 июля 2012 г.). «Капли в играх: 2D-видимость» . Проверено 9 мая 2014 г.

[bungiu-9] Перейти обратно: ^а ^б Бунгиу, Франциск; Хеммер, Майкл; Хершбергер, Джон; Хуанг, Кан; Креллер, Александр (2014). «Эффективное вычисление полигонов видимости». arXiv : 1403.3905 [ cs.CG ].

[hlogh-10] Хеффернан, Пол; Митчелл, Джозеф (1995). «Оптимальный алгоритм расчета видимости в плоскости» (PDF) . SIAM Journal по вычислительной технике . 24 (1): 184–201. дои : 10.1137/S0097539791221505 . hdl : 1813/8838 .

[so-11] Перейти обратно: ^а ^б Сури, Субхаш; О'Рурк, Джозеф (1986). Оптимальные в худшем случае алгоритмы построения многоугольников видимости с дырками . Симпозиум по вычислительной геометрии. АКМ . стр. 14–23. дои : 10.1145/10515.10517 .

[am-12] Аркин, Э .; Митчелл, Джозеф (1987). Алгоритм оптимальной видимости простого многоугольника со звездообразными отверстиями (Технический отчет). Корнелльский университет по исследованию операций и промышленной инженерии. 746.

[asano-13] Асано, Тецуо (1985). Эффективный алгоритм поиска полигона видимости для многоугольной области с дырками . Институт инженеров электроники, информации и связи. Том. 68. стр. 557–559.

[hershberger-14] Хершбергер, Джон (1989). «Нахождение верхнего конверта $n$ сегменты линий в $O(n\log n)$ время». Письма обработки информации . 33 (4): 169–174. doi : 10.1016/0020-0190(89)90136-1 .

[1]

[2]

[3]

[4]

[5]

[6]

[7]

[8]

[9]

[10]

[11]

[12]

[13]

[14]